Integrală definită prin exemple de părți. Rezolvarea integralelor online
Anterior, pentru o funcție dată, ghidată de diverse formule și reguli, am găsit derivata ei. Derivata are numeroase aplicatii: este viteza de miscare (sau, mai general, viteza oricarui proces); panta tangentei la graficul funcției; folosind derivata, puteți investiga funcția pentru monotonitate și extreme; Ajută la rezolvarea problemelor de optimizare.
Dar, alături de problema găsirii vitezei dintr-o lege cunoscută a mișcării, există și o problemă inversă - problema restabilirii legii mișcării dintr-o viteză cunoscută. Să luăm în considerare una dintre aceste probleme.
Exemplul 1 Un punct material se deplasează de-a lungul unei linii drepte, viteza mișcării sale la momentul t este dată de formula v=gt. Găsiți legea mișcării.
Soluţie. Fie s = s(t) legea de mișcare dorită. Se știe că s"(t) = v(t). Deci, pentru a rezolva problema, trebuie să alegeți o funcție s = s(t), a cărei derivată este egală cu gt. Este ușor de ghicit că \( s(t) = \frac(gt^ 2)(2) \) Într-adevăr
\(s"(t) = \left(\frac(gt^2)(2) \right)" = \frac(g)(2)(t^2)" = \frac(g)(2) \ cdot 2t=gt\)
Răspuns: \(s(t) = \frac(gt^2)(2) \)
Observăm imediat că exemplul este rezolvat corect, dar incomplet. Se obține \(s(t) = \frac(gt^2)(2) \). De fapt, problema are infinit de soluții: orice funcție de forma \(s(t) = \frac(gt^2)(2) + C \), unde C este o constantă arbitrară, poate servi drept lege a mișcare, deoarece \(\left (\frac(gt^2)(2) +C \right)" = gt \)
Pentru a face problema mai specifică, a trebuit să remediem situația inițială: să indicăm coordonatele punctului în mișcare la un moment dat, de exemplu, la t = 0. Dacă, de exemplu, s(0) = s 0 , atunci din egalitatea s(t) = (gt 2)/2 + C obținem: s(0) = 0 + C, adică C = s 0 . Acum legea mișcării este definită în mod unic: s(t) = (gt 2)/2 + s 0 .
În matematică, operațiilor reciproc inverse li se atribuie diferite nume, vin cu notații speciale, de exemplu: pătrarea (x 2) și extragerea rădăcinii pătrate (\(\sqrt(x) \)), sinus (sin x) și arcsinus ( arcsin x) și etc Procesul de găsire a derivatei față de o funcție dată se numește diferenţiere, și operația inversă, adică procesul de găsire a unei funcții printr-o derivată dată, - integrare.
Termenul „derivat” în sine poate fi justificat „într-un mod lumesc”: funcția y \u003d f (x) „produce în lume” o nouă funcție y” \u003d f ”(x). Funcția y \u003d f (x) acționează ca un „părinte”, dar matematicienii, desigur, nu o numesc „părinte” sau „producător”, ei spun că aceasta este, în raport cu funcția y " = f" (x) , imaginea primară sau antiderivată.
Definiție. O funcție y = F(x) se numește antiderivată pentru o funcție y = f(x) pe un interval X dacă \(x \in X \) satisface egalitatea F"(x) = f(x)
În practică, intervalul X nu este de obicei specificat, ci subînțeles (ca domeniul natural al funcției).
Să dăm exemple.
1) Funcția y \u003d x 2 este o antiderivată pentru funcția y \u003d 2x, deoarece pentru orice x egalitatea (x 2) "\u003d 2x este adevărată
2) Funcția y \u003d x 3 este o antiderivată pentru funcția y \u003d 3x 2, deoarece pentru orice x egalitatea (x 3)" \u003d 3x 2 este adevărată
3) Funcția y \u003d sin (x) este o antiderivată pentru funcția y \u003d cos (x), deoarece pentru orice x egalitatea (sin (x)) "= cos (x) este adevărată
Atunci când se găsesc antiderivate, precum și derivate, se folosesc nu numai formule, ci și unele reguli. Ele sunt direct legate de regulile corespunzătoare pentru calculul derivatelor.
Știm că derivata unei sume este egală cu suma derivatelor. Această regulă generează regula corespunzătoare pentru găsirea antiderivatelor.
Regula 1 Antiderivata unei sume este egală cu suma antiderivatelor.
Știm că factorul constant poate fi scos din semnul derivatei. Această regulă generează regula corespunzătoare pentru găsirea antiderivatelor.
Regula 2 Dacă F(x) este o antiderivată pentru f(x), atunci kF(x) este o antiderivată pentru kf(x).
Teorema 1. Dacă y = F(x) este antiderivată pentru funcția y = f(x), atunci antiderivată pentru funcția y = f(kx + m) este funcția \(y=\frac(1)(k)F (kx+m) \)
Teorema 2. Dacă y = F(x) este o antiderivată pentru o funcție y = f(x) pe un interval X, atunci funcția y = f(x) are infinite de antiderivate și toate au forma y = F(x) + C.
Metode de integrare
Metoda de înlocuire variabilă (metoda de înlocuire)
Metoda de integrare prin substituție constă în introducerea unei noi variabile de integrare (adică o substituție). În acest caz, integrala dată este redusă la o nouă integrală, care este tabelară sau reductibilă la aceasta. Nu există metode generale de selectare a substituțiilor. Capacitatea de a determina corect substituția este dobândită prin practică.
Fie necesar să se calculeze integrala \(\textstyle \int F(x)dx \). Să facem o substituție \(x= \varphi(t) \) unde \(\varphi(t) \) este o funcție care are o derivată continuă.
Atunci \(dx = \varphi " (t) \cdot dt \) și pe baza proprietății de invarianță a formulei de integrare integrală nedefinită, obținem formula de integrare a substituției:
\(\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt \)
Integrarea expresiilor precum \(\textstyle \int \sin^n x \cos^m x dx \)
Dacă m este impar, m > 0, atunci este mai convenabil să se facă substituția sin x = t.
Dacă n este impar, n > 0, atunci este mai convenabil să se facă substituția cos x = t.
Dacă n și m sunt pare, atunci este mai convenabil să se facă substituția tg x = t.
Integrare pe părți
Integrare pe părți - aplicând următoarea formulă pentru integrare:
\(\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du \)
sau:
\(\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx \)
Tabel de integrale nedefinite (antiderivate) ale unor funcții
$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) +C \;\; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(arcsin) x +C $$ $$ \int \frac(dx)(1+x^2 ) = \text(arctg) x +C $$ $$ \int \text(ch) x dx = \text(sh) x +C $$ $$ \int \text(sh) x dx = \text(ch) )x+C $$Integrare pe părți. Exemple de soluții
Buna din nou. Astăzi, în lecție, vom învăța cum să integrăm pe părți. Metoda de integrare pe părți este una dintre pietrele de temelie ale calculului integral. La test, examen, studentului i se oferă aproape întotdeauna să rezolve integrale de următoarele tipuri: integrala cea mai simplă (vezi articolul) sau o integrală pentru a schimba variabila (vezi articolul) sau integrala doar pe metoda de integrare pe părți.
Ca întotdeauna, la îndemână ar trebui să fie: Tabelul integralelorși Tabel de derivate. Dacă încă nu le aveți, vă rugăm să vizitați depozitul site-ului meu: Formule și tabele matematice. Nu mă voi sătura să repet - este mai bine să tipăriți totul. Voi încerca să prezint tot materialul într-un mod consistent, simplu și accesibil; nu există dificultăți deosebite în integrarea pe părți.
Ce problemă rezolvă integrarea pe părți? Metoda de integrare pe părți rezolvă o problemă foarte importantă, vă permite să integrați unele funcții care nu sunt în tabel, muncă funcții, iar în unele cazuri - și private. După cum ne amintim, nu există o formulă convenabilă: ![]() . Dar există acesta:
. Dar există acesta: ![]() este formula de integrare pe părți în persoană. Știu, știu, ești singurul - cu ea vom lucra toată lecția (este deja mai ușor).
este formula de integrare pe părți în persoană. Știu, știu, ești singurul - cu ea vom lucra toată lecția (este deja mai ușor).
Și imediat lista în studio. Integralele de următoarele tipuri sunt luate pe părți:
1) , ![]() , - logaritm, logaritm înmulțit cu un polinom.
, - logaritm, logaritm înmulțit cu un polinom.
2) ,![]() este o funcție exponențială înmulțită cu un polinom. Aceasta include, de asemenea, integrale precum - o funcție exponențială înmulțită cu un polinom, dar în practică este de 97 la sută, o literă drăguță „e” se etalează sub integrală. ... articolul se dovedește a fi ceva liric, ah da... a venit primăvara.
este o funcție exponențială înmulțită cu un polinom. Aceasta include, de asemenea, integrale precum - o funcție exponențială înmulțită cu un polinom, dar în practică este de 97 la sută, o literă drăguță „e” se etalează sub integrală. ... articolul se dovedește a fi ceva liric, ah da... a venit primăvara.
3) , ![]() , sunt funcții trigonometrice înmulțite cu un polinom.
, sunt funcții trigonometrice înmulțite cu un polinom.
4) , - funcții trigonometrice inverse („arcuri”), „arcuri”, înmulțite cu un polinom.
De asemenea, unele fracții sunt luate în părți, vom lua în considerare și exemplele corespunzătoare în detaliu.
Integrale ale logaritmilor
Exemplul 1
Clasic. Din când în când, această integrală poate fi găsită în tabele, dar nu este de dorit să folosiți un răspuns gata făcut, deoarece profesorul are beriberi în primăvară și va certa mult. Deoarece integrala luată în considerare nu este nicidecum tabelară - este luată în părți. Noi decidem:
Întrerupem soluția pentru explicații intermediare.
Folosim formula de integrare pe părți: ![]()
Formula se aplică de la stânga la dreapta
Ne uităm la partea stângă:. Evident, în exemplul nostru (și în toate celelalte pe care le vom lua în considerare), ceva trebuie notat cu , iar ceva cu .
În integralele de tipul luat în considerare, notăm întotdeauna logaritmul.
Din punct de vedere tehnic, proiectarea soluției este implementată după cum urmează, scriem în coloană:
Adică, pentru că am notat logaritmul, iar pentru - partea rămasă integrand.
Pasul următor: găsiți diferența:

Diferența este aproape aceeași cu derivata, am discutat deja cum să o găsim în lecțiile anterioare.
Acum găsim funcția . Pentru a găsi funcția este necesar să se integreze partea dreapta egalitate mai mica:

Acum deschidem soluția noastră și construim partea dreaptă a formulei: .
Apropo, iată un exemplu de soluție finală cu note mici:

Singurul moment din produs, am rearanjat imediat și, deoarece este obișnuit să scrieți multiplicatorul înainte de logaritm.
După cum puteți vedea, aplicarea formulei de integrare pe părți a redus soluția noastră la două integrale simple.
Vă rugăm să rețineți că în unele cazuri imediat dupa aplicarea formulei, se realizează în mod necesar o simplificare sub integrala rămasă - în exemplul luat în considerare, am redus integrandul cu „x”.
Hai să facem o verificare. Pentru a face acest lucru, trebuie să luați derivata răspunsului:
Se obține integrandul original, ceea ce înseamnă că integrala este rezolvată corect.
În timpul verificării, am folosit regula de diferențiere a produsului: ![]() . Și asta nu este o coincidență.
. Și asta nu este o coincidență.
Formula de integrare prin părți ![]() si formula
si formula ![]() Acestea sunt două reguli reciproc inverse.
Acestea sunt două reguli reciproc inverse.
Exemplul 2
Aflați integrala nedefinită.
Integrandul este produsul dintre logaritm și polinom.
Noi decidem.
![]()
Voi descrie din nou în detaliu procedura de aplicare a regulii, în viitor exemplele vor fi făcute mai pe scurt și, dacă întâmpinați dificultăți în a o rezolva singur, trebuie să reveniți la primele două exemple ale lecției. .
După cum sa menționat deja, pentru că este necesar să se desemneze logaritmul (faptul că este într-un grad nu contează). Notăm partea rămasă integrand.
Scriem într-o coloană:
Mai întâi găsim diferența:

Aici folosim regula de diferențiere a unei funcții complexe ![]() . Nu întâmplător, chiar la prima lecție a subiectului Integrală nedefinită. Exemple de soluții M-am concentrat pe faptul că, pentru a stăpâni integralele, trebuie să „puneți mâna” pe derivate. Derivatele vor trebui să se confrunte de mai multe ori.
. Nu întâmplător, chiar la prima lecție a subiectului Integrală nedefinită. Exemple de soluții M-am concentrat pe faptul că, pentru a stăpâni integralele, trebuie să „puneți mâna” pe derivate. Derivatele vor trebui să se confrunte de mai multe ori.
Acum găsim funcția , pentru aceasta integrăm partea dreapta egalitate mai mica:

Pentru integrare, am aplicat cea mai simplă formulă tabelară ![]()
Acum sunteți gata să aplicați formula ![]() . Îl deschidem cu un „asterisc” și „proiectăm” soluția în conformitate cu partea dreaptă:
. Îl deschidem cu un „asterisc” și „proiectăm” soluția în conformitate cu partea dreaptă:
Sub integrală, avem din nou un polinom pe logaritm! Prin urmare, soluția se întrerupe din nou și se aplică a doua oară regula integrării pe părți. Nu uitați că, în situații similare, logaritmul este întotdeauna notat.

Ar fi bine dacă în acest moment ați putea găsi pe cale orală cele mai simple integrale și derivate.

(1) Nu vă încurcați în semne! Foarte des se pierde aici un minus, de asemenea, rețineți că se aplică minusul pentru toti paranteză  , iar aceste paranteze trebuie deschise corect.
, iar aceste paranteze trebuie deschise corect.
(2) Extindeți parantezele. Simplificam ultima integrala.
(3) Luăm ultima integrală.
(4) „Păptănând” răspunsul.
Necesitatea de a aplica regula integrării pe părți de două ori (sau chiar de trei ori) nu este neobișnuită.
Și acum câteva exemple pentru o soluție independentă:
Exemplul 3
Aflați integrala nedefinită.
Acest exemplu se rezolva prin metoda schimbarii variabilei (sau subsumarea semnului diferential)! Și de ce nu - poți încerca să-l iei pe părți, obții un lucru amuzant.
Exemplul 4
Aflați integrala nedefinită.
Dar această integrală este integrată de părți (fracția promisă).
Acestea sunt exemple de auto-rezolvare, soluții și răspunsuri la sfârșitul lecției.
Se pare că în exemplele 3,4 integranții sunt similari, dar metodele de rezolvare sunt diferite! Aceasta este tocmai principala dificultate în stăpânirea integralelor - dacă alegeți metoda greșită de rezolvare a integralei, atunci vă puteți juca cu ea ore întregi, ca într-un puzzle adevărat. Prin urmare, cu cât rezolvi mai multe integrale, cu atât mai bine, cu atât testul și examenul vor fi mai ușor. În plus, în al doilea an vor exista ecuații diferențiale, iar fără experiență în rezolvarea integralelor și derivatelor nu este nimic de făcut acolo.
Prin logaritmi, poate mai mult decât suficient. Pentru o gustare, îmi pot aminti și că studenții de la tehnologie numesc sânii feminini logaritmi =). Apropo, este util să cunoaștem pe de rost graficele principalelor funcții elementare: sinus, cosinus, arc tangentă, exponent, polinoame de gradul trei, al patrulea etc. Nu, desigur, un prezervativ pe un glob
Nu o să trag, dar acum vă veți aminti multe din secțiune Grafice și funcții =).
Integrale ale exponentului înmulțite cu polinom
Regula generala:
Exemplul 5
Aflați integrala nedefinită.
![]()
Folosind un algoritm familiar, integrăm pe părți:


Dacă aveți dificultăți cu integrala, atunci ar trebui să reveniți la articol Metoda modificării variabilei în integrală nedefinită.
Singurul lucru de făcut este să „pieptănați” răspunsul:

Dar dacă tehnica ta de calcul nu este foarte bună, atunci lăsați cea mai profitabilă opțiune ca răspuns. ![]() sau chiar
sau chiar ![]()
Adică exemplul se consideră rezolvat atunci când se ia ultima integrală. Nu va fi o greșeală, este o altă problemă pe care profesorul o poate cere să simplifice răspunsul.
Exemplul 6
Aflați integrala nedefinită.
Acesta este un exemplu de do-it-yourself. Această integrală este integrată de două ori pe părți. O atenție deosebită trebuie acordată semnelor - este ușor să vă confundați în ele, ne amintim, de asemenea, că - o funcție complexă.
Nu sunt multe de spus despre expozant. Pot doar să adaug că exponențialul și logaritmul natural sunt funcții reciproc inverse, acesta sunt eu pe tema graficelor distractive ale matematicii superioare =) Stop-stop, nu vă faceți griji, lectorul este treaz.
Integrale ale funcțiilor trigonometrice înmulțite cu un polinom
Regula generala: reprezintă întotdeauna polinom
Exemplul 7
Aflați integrala nedefinită.
![]()
Integrarea pe părți:


Hmmm... și nimic de comentat.
Exemplul 8
Aflați integrala nedefinită ![]()
Acesta este un exemplu pentru o soluție do-it-yourself
Exemplul 9
Aflați integrala nedefinită
Un alt exemplu cu o fracție. Ca și în cele două exemple anterioare, un polinom este notat cu.
Integrarea pe părți: 

Dacă aveți dificultăți sau neînțelegeri în găsirea integralei, atunci vă recomand să participați la lecție Integrale ale funcțiilor trigonometrice.
Exemplul 10
Aflați integrala nedefinită ![]()
Acesta este un exemplu de do-it-yourself.
Sugestie: înainte de a utiliza metoda integrării prin părți, ar trebui să aplicați o formulă trigonometrică care transformă produsul a două funcții trigonometrice într-o singură funcție. Formula poate fi utilizată și în cursul aplicării metodei de integrare pe părți, cărora le este mai convenabil.
Asta, poate, este tot în acest paragraf. Dintr-un motiv oarecare, mi-am amintit o linie din imnul Departamentului de Fizică și Matematică „Și unda sinusoidală după val merge de-a lungul axei absciselor” ....
Integrale ale funcțiilor trigonometrice inverse.
Integrale ale funcțiilor trigonometrice inverse înmulțite cu un polinom
Regula generala: reprezintă întotdeauna funcția trigonometrică inversă.
Vă reamintesc că funcțiile trigonometrice inverse includ arcsinus, arccosinus, arctangent și arccotangent. De dragul conciziei, le voi numi „arcuri”

 la calculul integralei
la calculul integralei  , care se dovedește a fi mai simplu decât cel dat.
, care se dovedește a fi mai simplu decât cel dat. ,
, ,
, , Unde
, Unde  - polinom,
- polinom,  - numărul nu este egal cu zero
- numărul nu este egal cu zero denotă polinom
denotă polinom 
 .
. ,
, ,
, ,
, ,
, , Unde
, Unde  este un polinom.
este un polinom. desemna
desemna  , iar restul integrand prin
, iar restul integrand prin  :
: ,
, , Unde
, Unde  - numere.
- numere. desemna
desemna  și aplicați de două ori formula de integrare pe părți, revenind ca rezultat la integrala inițială, după care integrala inițială este exprimată din egalitate.
și aplicați de două ori formula de integrare pe părți, revenind ca rezultat la integrala inițială, după care integrala inițială este exprimată din egalitate. ; b)
; b)  .
.
 , Unde
, Unde  este un polinom de grad
este un polinom de grad  ,
, este un polinom de grad
este un polinom de grad
 .
. altfel (daca
altfel (daca  ) o fracție rațională se numește gresit.
) o fracție rațională se numește gresit. și o fracție rațională proprie prin împărțirea numărătorului la numitor conform regulii împărțirii polinoamelor:
și o fracție rațională proprie prin împărțirea numărătorului la numitor conform regulii împărțirii polinoamelor: ,
, este partea întreagă a diviziunii,
este partea întreagă a diviziunii,  este o fracție rațională proprie,
este o fracție rațională proprie,  - restul diviziei.
- restul diviziei. ;
; ;
; ;
; ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 sunt numere reale și
sunt numere reale și  (adică trinomul pătrat din numitorul III și IV al fracțiilor nu are rădăcini - discriminantul este negativ) se numesc cele mai simple fracții raționale I, II, III și IV tipuri.
(adică trinomul pătrat din numitorul III și IV al fracțiilor nu are rădăcini - discriminantul este negativ) se numesc cele mai simple fracții raționale I, II, III și IV tipuri. .
. .
. . Integrala după înlocuire este împărțită în două integrale. Prima integrală se calculează prin extragerea derivatei numitorului din numărător, care dă o integrală tabelară, iar a doua integrală este transformată în forma
. Integrala după înlocuire este împărțită în două integrale. Prima integrală se calculează prin extragerea derivatei numitorului din numărător, care dă o integrală tabelară, iar a doua integrală este transformată în forma  , deoarece
, deoarece  , care dă și o integrală de tabel.
, care dă și o integrală de tabel.

 ;
; . Integrala după înlocuire este împărțită în două integrale. Prima integrală se calculează prin înlocuire
. Integrala după înlocuire este împărțită în două integrale. Prima integrală se calculează prin înlocuire  , iar al doilea cu ajutorul relațiilor de recurență.
, iar al doilea cu ajutorul relațiilor de recurență. ; b)
; b)  ; în)
; în)  .
. .
. corespunde unei fracții din formă
corespunde unei fracții din formă  ;
; suma corespunzătoare
suma corespunzătoare  fracții ale formei
fracții ale formei corespunde unei fracțiuni din formă
corespunde unei fracțiuni din formă  ;
; suma corespunzătoare
suma corespunzătoare  fracții ale formei
fracții ale formei . Echivalarea coeficienților la aceleași puteri
. Echivalarea coeficienților la aceleași puteri  în polinoamele părților din stânga și din dreapta, obținem un sistem de ecuații liniare. Rezolvând sistemul, determinăm coeficienții incerti.
în polinoamele părților din stânga și din dreapta, obținem un sistem de ecuații liniare. Rezolvând sistemul, determinăm coeficienții incerti. în stânga și în dreapta oricărui număr, obținem egalitatea corectă, care este liniară în raport cu coeficienții necunoscuți. Înlocuind atâtea valori
în stânga și în dreapta oricărui număr, obținem egalitatea corectă, care este liniară în raport cu coeficienții necunoscuți. Înlocuind atâtea valori  , câți coeficienți necunoscuți, obținem un sistem de ecuații liniare. În loc de
, câți coeficienți necunoscuți, obținem un sistem de ecuații liniare. În loc de  orice numere pot fi înlocuite în părțile din stânga și din dreapta, cu toate acestea, este mai convenabil să înlocuiți rădăcinile numitorilor fracțiilor.
orice numere pot fi înlocuite în părțile din stânga și din dreapta, cu toate acestea, este mai convenabil să înlocuiți rădăcinile numitorilor fracțiilor. ; b)
; b)  ; în)
; în)  .
. .
.
 .
. , primim:
, primim:



 .
. .
. .
. .
. , obținem sistemul:
, obținem sistemul:








 .
.
 .
. .
. .
. valori parțiale la care factorii dispar, adică substituim aceste valori în ultima expresie și obținem trei ecuații:
valori parțiale la care factorii dispar, adică substituim aceste valori în ultima expresie și obținem trei ecuații:
 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.


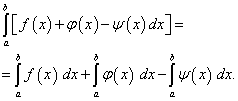 (42)
(42)




