Co to są wektory własne i wartości własne. Wartości własne (liczby) i wektory własne Przykłady rozwiązań

Jak wstawić wzory matematyczne na stronie?

Jeśli kiedykolwiek zajdzie potrzeba dodania jednej lub dwóch formuł matematycznych do strony internetowej, najłatwiej jest to zrobić w sposób opisany w artykule: formuły matematyczne można łatwo wstawić do witryny w postaci obrazów automatycznie generowanych przez Wolfram Alpha. Oprócz prostoty, ta uniwersalna metoda pomoże poprawić widoczność witryny w wyszukiwarkach. To działa od dawna (i myślę, że będzie działać na zawsze), ale jest moralnie przestarzałe.

Jeśli stale używasz formuł matematycznych w swojej witrynie, zalecam użycie MathJax, specjalnej biblioteki JavaScript, która wyświetla notację matematyczną w przeglądarkach internetowych przy użyciu znaczników MathML, LaTeX lub ASCIIMathML.

Istnieją dwa sposoby rozpoczęcia korzystania z MathJax: (1) używając prostego kodu, możesz szybko połączyć skrypt MathJax ze swoją witryną, który zostanie automatycznie załadowany ze zdalnego serwera we właściwym czasie (lista serwerów); (2) prześlij skrypt MathJax ze zdalnego serwera na swój serwer i połącz go ze wszystkimi stronami swojej witryny. Druga metoda jest bardziej złożona i czasochłonna i pozwoli przyspieszyć ładowanie stron Twojej witryny, a jeśli nadrzędny serwer MathJax stanie się z jakiegoś powodu chwilowo niedostępny, nie wpłynie to w żaden sposób na Twoją własną witrynę. Mimo tych zalet wybrałem pierwszą metodę, ponieważ jest prostsza, szybsza i nie wymaga umiejętności technicznych. Podążaj za moim przykładem, a w ciągu 5 minut będziesz mógł korzystać ze wszystkich funkcji MathJax na swojej stronie.

Możesz połączyć skrypt biblioteki MathJax ze zdalnego serwera, używając dwóch opcji kodu pobranych z głównej witryny MathJax lub ze strony dokumentacji:

Jedną z tych opcji kodu należy skopiować i wkleić do kodu swojej strony internetowej, najlepiej między tagami oraz lub zaraz po tagu . Zgodnie z pierwszą opcją MathJax ładuje się szybciej i mniej spowalnia stronę. Ale druga opcja automatycznie śledzi i ładuje najnowsze wersje MathJax. Jeśli wstawisz pierwszy kod, będzie on wymagał okresowej aktualizacji. Jeśli wkleisz drugi kod, strony będą ładować się wolniej, ale nie będziesz musiał stale monitorować aktualizacji MathJax.

Najprostszym sposobem połączenia MathJax jest Blogger lub WordPress: w panelu sterowania witryny dodaj widżet przeznaczony do wstawiania kodu JavaScript innej firmy, skopiuj do niego pierwszą lub drugą wersję powyższego kodu ładowania i umieść widżet bliżej początek szablonu (nawiasem mówiąc, nie jest to wcale konieczne, ponieważ skrypt MathJax jest ładowany asynchronicznie). To wszystko. Teraz poznaj składnię znaczników MathML, LaTeX i ASCIIMathML i możesz osadzać formuły matematyczne na swoich stronach internetowych.

Każdy fraktal jest zbudowany zgodnie z pewną zasadą, która jest konsekwentnie stosowana nieograniczoną liczbę razy. Każdy taki czas nazywany jest iteracją.

Iteracyjny algorytm konstruowania gąbki Mengera jest dość prosty: oryginalny sześcian o boku 1 jest podzielony płaszczyznami równoległymi do jego ścian na 27 równych sześcianów. Jeden środkowy sześcian i 6 kostek przylegających do niego wzdłuż ścian zostaje z niego usuniętych. Okazuje się, że zestaw składający się z 20 pozostałych mniejszych kostek. Robiąc to samo z każdą z tych kostek, otrzymujemy zestaw składający się z 400 mniejszych kostek. Kontynuując ten proces w nieskończoność, otrzymujemy gąbkę Mengera.

UKŁAD JEDNORAZOWYCH RÓWNAŃ LINIOWYCH

Układ jednorodnych równań liniowych jest układem postaci

Wiadomo, że w tym przypadku , dlatego wszystkie elementy jednej z kolumn w tych wyznacznikach są równe zeru.

Ponieważ niewiadome znajdują się za pomocą wzorów , to w przypadku, gdy Δ ≠ 0, układ ma unikalne rozwiązanie zerowe x = y = z= 0. Jednak w wielu problemach interesujące jest pytanie, czy system jednorodny ma rozwiązania inne niż zero.

Twierdzenie. Aby układ równań liniowych jednorodnych miał rozwiązanie niezerowe, konieczne i wystarczające jest, aby Δ ≠ 0.

Tak więc, jeśli wyznacznik wynosi Δ ≠ 0, to system ma unikalne rozwiązanie. Jeżeli Δ ≠ 0, to układ równań liniowych jednorodnych ma nieskończoną liczbę rozwiązań.

Przykłady.

Wektory własne i macierzowe wartości własne

Niech będzie dana macierz kwadratowa , X to pewna kolumna macierzy, której wysokość pokrywa się z rzędem macierzy A. .

W wielu problemach należy wziąć pod uwagę równanie dla X

gdzie λ jest pewną liczbą. Jest oczywiste, że dla dowolnego λ to równanie ma rozwiązanie zerowe.

Nazywa się liczbę λ, dla której to równanie ma niezerowe rozwiązania wartość własna macierze A, a X dla takiego λ nazywamy własny wektor macierze A.

Znajdźmy wektor własny macierzy A. Ponieważ mi∙X=X, to równanie macierzowe można zapisać jako lub . W rozszerzonej formie równanie to można zapisać jako układ równań liniowych. Naprawdę .

I dlatego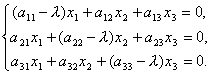

Otrzymaliśmy więc układ jednorodnych równań liniowych do określania współrzędnych x 1, x2, x 3 wektor X. Aby układ miał rozwiązania niezerowe, konieczne i wystarczające jest, aby wyznacznik układu był równy zeru, tj.

Jest to równanie trzeciego stopnia względem λ. To jest nazwane równanie charakterystyczne macierze A i służy do określenia wartości własnych λ.

Każda wartość własna λ odpowiada wektorowi własnemu X, którego współrzędne są wyznaczane z układu przy odpowiedniej wartości λ.

Przykłady.

ALGEBRA WEKTOROWA. KONCEPCJA WEKTORA

Podczas studiowania różnych gałęzi fizyki istnieją wielkości, które są całkowicie określone przez ustawienie ich wartości liczbowych, na przykład długość, powierzchnia, masa, temperatura itp. Takie wartości nazywane są skalarnymi. Jednak oprócz nich istnieją również wielkości, dla których określenia oprócz wartości liczbowej konieczna jest również znajomość ich kierunku w przestrzeni, na przykład siła działająca na ciało, prędkość i przyspieszenie ciała poruszającego się w przestrzeni, natężenia pola magnetycznego w danym punkcie przestrzeni itp. Wielkości takie nazywane są wielkościami wektorowymi.

Wprowadźmy ścisłą definicję.

Segment kierunkowy Nazwijmy odcinek, względem którego końców wiadomo, który z nich jest pierwszy, a który drugi.

Wektor nazywamy odcinek skierowany, mający określoną długość, tj. Jest to odcinek o określonej długości, w którym jeden z ograniczających go punktów przyjmuje się za początek, a drugi za koniec. Jeśli A jest początkiem wektora, B jest jego końcem, to wektor oznaczany jest symbolem, ponadto często wektor oznaczany jest pojedynczą literą . Na rysunku wektor jest oznaczony segmentem, a jego kierunek strzałką.

moduł lub długie wektor nazywany jest długością segmentu skierowanego, który go definiuje. Oznaczone przez || lub ||.

Tak zwany wektor zerowy, którego początek i koniec pokrywają się, będzie również nazywany wektorami. Jest zaznaczone. Wektor zerowy nie ma określonego kierunku, a jego moduł jest równy zeru ||=0.

Wektory i są nazywane współliniowy jeśli znajdują się na tej samej linii lub na liniach równoległych. W tym przypadku, jeśli wektory i są jednakowo skierowane, napiszemy , przeciwnie.

Nazywamy wektory leżące na liniach prostych równoległych do tej samej płaszczyzny współpłaszczyznowy.

Dwa wektory i są nazywane równy jeśli są współliniowe, mają ten sam kierunek i są równej długości. W takim przypadku napisz.

Z definicji równości wektorów wynika, że ​​wektor można przesuwać równolegle do siebie, umieszczając jego początek w dowolnym punkcie przestrzeni.

Na przykład.

OPERACJE LINIOWE NA WEKTORACH

1. Mnożenie wektora przez liczbę.

   Iloczyn wektora przez liczbę λ jest nowym wektorem takim, że:

   Iloczyn wektora i liczby λ jest oznaczony przez .

   

   Na przykład, jest wektorem skierowanym w tym samym kierunku co wektor i mającym połowę długości wektora .

   Wprowadzona operacja ma następujące znaczenie nieruchomości:

2. Dodawanie wektorów.

   Niech i będą dwoma dowolnymi wektorami. Weź dowolny punkt O i skonstruować wektor . Po tym, od punktu A odłóż wektor . Nazywa się wektor łączący początek pierwszego wektora z końcem drugiego suma tych wektorów i jest oznaczony .

   

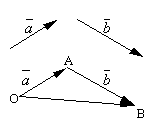
   Sformułowana definicja dodawania wektorów nazywa się reguła równoległoboku, ponieważ tę samą sumę wektorów można otrzymać w następujący sposób. Odłóż na bok O wektory i . Skonstruuj równoległobok na tych wektorach OAB. Ponieważ wektory , to wektor , który jest przekątną równoległoboku poprowadzonego z wierzchołka O, będzie oczywiście sumą wektorów .

   

   Łatwo sprawdzić następujące rzeczy właściwości dodawania wektorów.

3. Różnica wektorów.

   Nazywamy wektor współliniowy z danym wektorem , równej długości i przeciwnie skierowany naprzeciwko wektor dla wektora i jest oznaczony przez . Wektor przeciwny można uznać za wynik mnożenia wektora przez liczbę λ = –1: .

Wektor własny macierzy kwadratowej to taki, który po pomnożeniu przez daną macierz daje wektor współliniowy. Mówiąc prościej, gdy macierz jest mnożona przez wektor własny, ten ostatni pozostaje taki sam, ale pomnożony przez pewną liczbę.

Definicja

Wektor własny to niezerowy wektor V, który po pomnożeniu przez macierz kwadratową M staje się sobą, powiększonym o pewną liczbę λ. W notacji algebraicznej wygląda to następująco:

M × V = λ × V,

gdzie λ jest wartością własną macierzy M.

Rozważmy przykład liczbowy. Dla wygody pisania liczby w macierzy będą oddzielone średnikiem. Powiedzmy, że mamy macierz:

• M = 0; cztery;
• 6; 10.

Pomnóżmy to przez wektor kolumnowy:

• V = -2;

Mnożąc macierz przez wektor kolumnowy, otrzymujemy również wektor kolumnowy. W ścisłym języku matematycznym wzór na pomnożenie macierzy 2 × 2 przez wektor kolumnowy wyglądałby następująco:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 oznacza element macierzy M, stojący w pierwszym wierszu i pierwszej kolumnie, a M22 to element znajdujący się w drugim wierszu i drugiej kolumnie. Dla naszej macierzy elementy te to M11=0, M12=4, M21=6, M22 10. Dla wektora kolumnowego wartości te to V11= –2, V21=1. Zgodnie z tym wzorem otrzymujemy: wynik iloczynu macierzy kwadratowej przez wektor:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Dla wygody zapisujemy wektor kolumnowy w wierszu. Tak więc pomnożyliśmy macierz kwadratową przez wektor (-2; 1), co dało wektor (4; -2). Oczywiście jest to ten sam wektor pomnożony przez λ = -2. Lambda w tym przypadku oznacza wartość własną macierzy.

Wektor własny macierzy jest wektorem współliniowym, czyli obiektem, który nie zmienia swojego położenia w przestrzeni, gdy jest mnożony przez macierz. Pojęcie współliniowości w algebrze wektorów jest podobne do pojęcia równoległości w geometrii. W interpretacji geometrycznej wektory współliniowe są równoległymi skierowanymi segmentami o różnych długościach. Od czasów Euklidesa wiemy, że pojedyncza prosta ma nieskończoną liczbę równoległych do niej prostych, więc logiczne jest założenie, że każda macierz ma nieskończoną liczbę wektorów własnych.

Z poprzedniego przykładu widać, że zarówno (-8; 4), jak i (16; -8) oraz (32, -16) mogą być wektorami własnymi. Wszystko to są wektory współliniowe odpowiadające wartości własnej λ = -2. Mnożąc oryginalną macierz przez te wektory, nadal otrzymamy wektor, który różni się od oryginału 2 razy. Dlatego przy rozwiązywaniu problemów ze znalezieniem wektora własnego wymagane jest znalezienie tylko liniowo niezależnych obiektów wektorowych. Najczęściej dla macierzy n × n istnieje n-ta liczba wektorów własnych. Nasz kalkulator jest przeznaczony do analizy macierzy kwadratowych drugiego rzędu, więc prawie zawsze zostaną znalezione dwa wektory własne, chyba że się pokrywają.

W powyższym przykładzie znaliśmy z góry wektor własny oryginalnej macierzy i wizualnie określiliśmy liczbę lambda. Jednak w praktyce wszystko dzieje się na odwrót: na początku są wartości własne, a dopiero potem wektory własne.

Algorytm rozwiązania

Spójrzmy ponownie na pierwotną macierz M i spróbujmy znaleźć oba jej wektory własne. Macierz wygląda więc następująco:

• M = 0; cztery;
• 6; 10.

Na początek musimy wyznaczyć wartość własną λ, dla której musimy obliczyć wyznacznik następującej macierzy:

• (0 - λ); cztery;
• 6; (10 - λ).

Macierz tę uzyskuje się odejmując nieznaną λ od elementów na głównej przekątnej. Wyznacznik określa się za pomocą standardowego wzoru:

• detA = M11 × M21 − M12 × M22
• det A = (0 − λ) × (10 − λ) − 24

Ponieważ nasz wektor nie może być zerem, przyjmujemy wynikowe równanie jako liniowo zależne i przyrównujemy nasz wyznacznik detA do zera.

(0 - λ) × (10 - λ) - 24 = 0

Otwórzmy nawiasy i uzyskajmy charakterystyczne równanie macierzy:

λ 2 - 10 λ - 24 = 0

Jest to standardowe równanie kwadratowe, które należy rozwiązać za pomocą dyskryminatora.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Pierwiastek dyskryminatora to sqrt(D) = 14, więc λ1 = -2, λ2 = 12. Teraz dla każdej wartości lambda musimy znaleźć wektor własny. Wyraźmy współczynniki układu dla λ = -2.

• M - λ × mi = 2; cztery;
• 6; 12.

W tym wzorze E jest macierzą tożsamości. Na podstawie otrzymanej macierzy układamy układ równań liniowych:

2x + 4y = 6x + 12y

gdzie x i y są elementami wektora własnego.

Zbierzmy wszystkie X po lewej i wszystkie Y po prawej. Oczywiście - 4x = 8y. Podziel wyrażenie przez -4 i uzyskaj x = -2y. Teraz możemy wyznaczyć pierwszy wektor własny macierzy, biorąc dowolne wartości niewiadomych (pamiętajmy o nieskończoności liniowo zależnych wektorów własnych). Weźmy y = 1, następnie x = -2. Dlatego pierwszy wektor własny wygląda jak V1 = (–2; 1). Wróć do początku artykułu. To właśnie przez ten obiekt wektorowy pomnożyliśmy macierz, aby zademonstrować koncepcję wektora własnego.

Teraz znajdźmy wektor własny dla λ = 12.

• M - λ × E = -12; cztery
• 6; -2.

Skomponujmy ten sam układ równań liniowych;

• -12x + 4y = 6x - 2y
• -18x = -6y
• 3x=y.

Teraz weźmy x = 1, stąd y = 3. Zatem drugi wektor własny wygląda jak V2 = (1; 3). Podczas mnożenia oryginalnej macierzy przez ten wektor wynikiem zawsze będzie ten sam wektor pomnożony przez 12. To kończy algorytm rozwiązania. Teraz wiesz, jak ręcznie zdefiniować wektor własny macierzy.

• wyznacznik;
• ślad, czyli suma elementów na głównej przekątnej;
• rangę, czyli maksymalną liczbę liniowo niezależnych wierszy/kolumn.

Program działa według powyższego algorytmu, minimalizując proces rozwiązania. Należy zaznaczyć, że w programie lambda jest oznaczona literą „c”. Spójrzmy na przykład liczbowy.

Przykład programu

Spróbujmy zdefiniować wektory własne dla następującej macierzy:

• M=5; 13;
• 4; 14.

Wpiszmy te wartości do komórek kalkulatora i uzyskajmy odpowiedź w następującej formie:

• Ranga matrycy: 2;
• Wyznacznik macierzy: 18;
• Ślad matrycy: 19;
• Obliczenie wektora własnego: c 2 − 19,00c + 18,00 (równanie charakterystyczne);
• Obliczenie wektora własnego: 18 (pierwsza wartość lambda);
• Obliczenie wektora własnego: 1 (druga wartość lambda);
• Układ równań wektora 1: -13x1 + 13y1 = 4x1 − 4y1;
• Układ równań wektora 2: 4x1 + 13y1 = 4x1 + 13y1;
• Wektor własny 1: (1; 1);
• Wektor własny 2: (-3,25; 1).

W ten sposób otrzymaliśmy dwa liniowo niezależne wektory własne.

Wniosek

Algebra liniowa i geometria analityczna to standardowe przedmioty dla każdego studenta pierwszego roku inżynierii. Duża liczba wektorów i macierzy przeraża, a przy tak kłopotliwych obliczeniach łatwo popełnić błąd. Nasz program pozwoli uczniom sprawdzić swoje obliczenia lub automatycznie rozwiązać problem znalezienia wektora własnego. W naszym katalogu są inne kalkulatory algebry liniowej, wykorzystaj je w swojej nauce lub pracy.

Definicja 9.3. Wektor X nazywa własny wektor macierze ALE jeśli jest taka liczba λ, że zachodzi równość: ALE X= λ X, to znaczy wynik zastosowania do X transformacja liniowa dana przez macierz ALE, to pomnożenie tego wektora przez liczbę λ . Sam numer λ nazywa własny numer macierze ALE.

Podstawianie do wzorów (9.3) x` j = λ x j , otrzymujemy układ równań do wyznaczania współrzędnych wektora własnego:

. (9.5)

Ten liniowy układ jednorodny będzie miał nietrywialne rozwiązanie tylko wtedy, gdy jego głównym wyznacznikiem jest 0 (reguła Cramera). Pisząc ten warunek w postaci:

otrzymujemy równanie do wyznaczania wartości własnych λ nazywa równanie charakterystyczne. W skrócie można to przedstawić następująco:

| A-λE | = 0, (9.6)

ponieważ jego lewa strona jest wyznacznikiem macierzy A-λE. Wielomian względem λ | A-λE| nazywa charakterystyczny wielomian macierze

Własności wielomianu charakterystycznego:

1) Wielomian charakterystyczny transformacji liniowej nie zależy od wyboru bazy. Dowód. (patrz (9.4)), ale W konsekwencji, . Nie zależy więc od wyboru bazy. Stąd i | A-λE| nie zmienia się po przejściu na nową podstawę.

2) Jeśli macierz ALE transformacja liniowa jest symetryczny(tych. ij = ji), to wszystkie pierwiastki równania charakterystycznego (9.6) są liczbami rzeczywistymi.

Własności wartości własnych i wektorów własnych:

1) Jeśli wybierzemy bazę z wektorów własnych x1, x2, x3 odpowiadające wartościom własnym λ 1 , λ 2 , λ 3 macierze ALE, to w tej bazie transformacja liniowa A ma macierz diagonalną:

(9.7) Dowód tej własności wynika z definicji wektorów własnych.

2) Jeśli wartości własne transformacji ALE są różne, to odpowiadające im wektory własne są liniowo niezależne.

3) Jeśli charakterystyczny wielomian macierzy ALE ma trzy różne pierwiastki, to w jakiejś bazie macierz ALE ma diagonalny kształt.

Znajdźmy wartości własne i wektory własne macierzy Utwórzmy równanie charakterystyczne: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Znajdź współrzędne wektorów własnych odpowiadających każdej znalezionej wartości λ. Z (9.5) wynika, że ​​jeśli X (1) ={x 1 , x 2 , x 3) jest wektorem własnym odpowiadającym λ 1 = -2, zatem

jest systemem współpracującym, ale nieokreślonym. Jego rozwiązanie można zapisać jako X (1) ={a,0,-a), gdzie a jest dowolną liczbą. W szczególności, jeśli tego potrzebujesz | x (1) |=1, X (1) =

Podstawianie do systemu (9.5) λ 2 = 3, otrzymujemy układ wyznaczania współrzędnych drugiego wektora własnego - x (2) ={y1,y2,y3}:

, gdzie X (2) ={b,-b,b) lub pod warunkiem | x (2) |=1, x (2) =

Do λ 3 = 6 znajdź wektor własny x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) lub w wersji znormalizowanej

x (3) = Można zauważyć, że X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = pne- 2pne + pne= 0. Zatem wektory własne tej macierzy są parami ortogonalne.

Wykład 10

Formy kwadratowe i ich związek z macierzami symetrycznymi. Własności wektorów własnych i wartości własnych macierzy symetrycznej. Redukcja formy kwadratowej do postaci kanonicznej.

Definicja 10.1.forma kwadratowa zmienne rzeczywiste x 1, x 2,…, x rz nazywamy wielomian drugiego stopnia względem tych zmiennych, który nie zawiera wyrazu wolnego i wyrazów pierwszego stopnia.

Przykłady form kwadratowych:

(n = 2),

(n = 3). (10.1)

Przypomnij sobie definicję macierzy symetrycznej podaną na ostatnim wykładzie:

Definicja 10.2. Nazywa się macierz kwadratowa symetryczny, jeśli , to znaczy, jeśli elementy macierzy symetryczne względem głównej przekątnej są równe.

Własności wartości własnych i wektorów własnych macierzy symetrycznej:

1) Wszystkie wartości własne macierzy symetrycznej są rzeczywiste.

Dowód (za n = 2).

Niech macierz ALE wygląda jak: . Zróbmy charakterystyczne równanie:

(10.2) Znajdź wyróżnik:

Dlatego równanie ma tylko rzeczywiste pierwiastki.

2) Wektory własne macierzy symetrycznej są ortogonalne.

Dowód (za n= 2).

Współrzędne wektorów własnych i muszą spełniać równania.