Mik azok a sajátvektorok és sajátértékek. Sajátértékek (számok) és sajátvektorok. Példák megoldásokra

Hogyan lehet matematikai képleteket beilleszteni a webhelyre?

Ha valaha egy vagy két matematikai képletet kell hozzáadnia egy weboldalhoz, akkor ezt a legegyszerűbben a cikkben leírtak szerint teheti meg: a matematikai képletek könnyen beilleszthetők az oldalra képek formájában, amelyeket Wolfram Alpha automatikusan generál. Az egyszerűség mellett ez az univerzális módszer segít javítani a webhely láthatóságát a keresőmotorokban. Régóta működik (és szerintem örökké működni fog), de erkölcsileg elavult.

Ha folyamatosan matematikai képleteket használ a webhelyén, akkor azt javaslom, hogy használja a MathJax-ot, egy speciális JavaScript-könyvtárat, amely MathML, LaTeX vagy ASCIIMathML jelölést használó webböngészőkben jeleníti meg a matematikai jelöléseket.

A MathJax használatának két módja van: (1) egy egyszerű kód segítségével gyorsan csatlakoztathat egy MathJax szkriptet a webhelyéhez, amely a megfelelő időben automatikusan betöltődik egy távoli szerverről (szerverek listája); (2) töltse fel a MathJax szkriptet egy távoli szerverről a szerverére, és csatlakoztassa webhelye összes oldalához. A második módszer bonyolultabb és időigényesebb, és lehetővé teszi, hogy felgyorsítsa webhelye oldalainak betöltését, és ha a szülő MathJax szerver valamilyen okból átmenetileg elérhetetlenné válik, az semmilyen módon nem érinti a saját webhelyét. Ezen előnyök ellenére az első módszert választottam, mivel az egyszerűbb, gyorsabb és nem igényel technikai ismereteket. Kövesse a példámat, és 5 percen belül használhatja a MathJax összes funkcióját webhelyén.

A MathJax könyvtár szkriptjét távoli szerverről csatlakoztathatja a MathJax fő webhelyéről vagy a dokumentációs oldalról származó két kódopció használatával:

Ezen kódopciók egyikét ki kell másolni és be kell illeszteni a weboldal kódjába, lehetőleg a címkék közé és vagy közvetlenül a címke után . Az első opció szerint a MathJax gyorsabban tölt be és kevésbé lassítja az oldalt. De a második lehetőség automatikusan követi és betölti a MathJax legújabb verzióit. Ha beírja az első kódot, akkor azt rendszeresen frissíteni kell. Ha beilleszti a második kódot, akkor az oldalak lassabban töltődnek be, de nem kell folyamatosan figyelnie a MathJax frissítéseit.

A MathJax csatlakoztatásának legegyszerűbb módja a Blogger vagy a WordPress: a webhely vezérlőpultján adjon hozzá egy widgetet, amely harmadik fél JavaScript kódjának beillesztésére szolgál, másolja bele a fenti betöltési kód első vagy második verzióját, és helyezze közelebb a widgetet a a sablon eleje (egyébként ez egyáltalán nem szükséges, mivel a MathJax szkript aszinkron módon töltődik be). Ez minden. Most tanulja meg a MathML, LaTeX és ASCIIMathML jelölési szintaxisát, és máris beágyazhat matematikai képleteket weboldalaiba.

Bármely fraktál egy bizonyos szabály szerint épül fel, amelyet következetesen korlátlan számú alkalommal alkalmaznak. Minden ilyen időt iterációnak nevezünk.

A Menger-szivacs elkészítésének iteratív algoritmusa meglehetősen egyszerű: az 1-es oldalú eredeti kockát a lapjaival párhuzamos síkok 27 egyenlő kockára osztják. Egy központi kockát és a lapok mentén szomszédos 6 kockát eltávolítanak róla. Kiderült, hogy egy készlet 20 megmaradt kisebb kockából áll. Minden egyes kockával ugyanezt megtéve egy 400 kisebb kockából álló készletet kapunk. Ezt a folyamatot a végtelenségig folytatva megkapjuk a Menger szivacsot.

HOMOGÉN LINEÁRIS EGYENLETRENDSZER

A homogén lineáris egyenletrendszer egy alakrendszer

Egyértelmű, hogy ebben az esetben , mert ezekben a determinánsokban az egyik oszlop minden eleme nullával egyenlő.

Mivel az ismeretleneket a képletek találják meg , akkor abban az esetben, ha Δ ≠ 0, a rendszernek egyedi nulla megoldása van x = y = z= 0. Sok feladatban azonban érdekes az a kérdés, hogy egy homogén rendszernek van-e nullától eltérő megoldása.

Tétel. Ahhoz, hogy egy lineáris homogén egyenletrendszernek nullától eltérő megoldása legyen, szükséges és elegendő, hogy Δ ≠ 0.

Tehát, ha a determináns Δ ≠ 0, akkor a rendszernek egyedi megoldása van. Ha Δ ≠ 0, akkor a lineáris homogén egyenletrendszernek végtelen számú megoldása van.

Példák.

Sajátvektorok és mátrix sajátértékek

Legyen adott egy négyzetes mátrix , x olyan mátrixoszlop, amelynek magassága egybeesik a mátrix sorrendjével A. .

Sok probléma esetén figyelembe kell venni a for egyenletet x

ahol λ valamilyen szám. Nyilvánvaló, hogy bármely λ esetén ennek az egyenletnek nulla megoldása van.

Azt a λ számot nevezzük, amelyre ennek az egyenletnek nullától eltérő megoldásai vannak sajátérték mátrixok A, a x mert az ilyen λ-t nevezzük saját vektor mátrixok A.

Keressük meg a mátrix sajátvektorát A. Mert a E∙X=X, akkor a mátrixegyenlet átírható így vagy . Kibővített formában ez az egyenlet átírható lineáris egyenletrendszerré. Igazán .

És ezért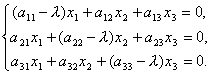

Így kaptunk egy homogén lineáris egyenletrendszert a koordináták meghatározásához x 1, x2, x 3 vektor x. Ahhoz, hogy a rendszernek nullától eltérő megoldásai legyenek, szükséges és elegendő, hogy a rendszer determinánsa nullával egyenlő legyen, azaz.

Ez egy 3. fokú egyenlet λ-hoz képest. Ezt hívják karakterisztikus egyenlet mátrixok Aés a λ sajátértékek meghatározására szolgál.

Minden λ sajátérték egy sajátvektornak felel meg x, amelynek koordinátáit a rendszerből a megfelelő λ értéknél határozzuk meg.

Példák.

VEKTOR ALGEBRA. VEKTOR FOGALOM

A fizika különféle ágainak tanulmányozása során vannak olyan mennyiségek, amelyeket teljes mértékben meghatároznak számértékeik megadásával, például hosszúság, terület, tömeg, hőmérséklet stb. Az ilyen értékeket skalárnak nevezzük. Rajtuk kívül azonban vannak olyan mennyiségek is, amelyek meghatározásához a számértéken kívül tudni kell térbeli irányukat is, például a testre ható erőt, a sebességet és a gyorsulást. a testnek a térben való mozgása során, a mágneses térerősség a tér adott pontjában stb. Az ilyen mennyiségeket vektormennyiségeknek nevezzük.

Vezessünk be egy szigorú definíciót.

Irányított szegmens Nevezzünk meg egy szegmenst, amelynek végeihez képest ismert, hogy melyik az első és melyik a második.

Vektor irányított szakaszt nevezünk, amelynek meghatározott hosszúsága van, pl. Ez egy bizonyos hosszúságú szegmens, amelyben az egyik korlátozó pont a kezdet, a második pedig a vég. Ha egy A a vektor kezdete, B a vége, akkor a vektort a szimbólum jelöli, ráadásul a vektort gyakran egyetlen betűvel jelöljük. Az ábrán a vektort egy szakasz, az irányát pedig egy nyíl jelzi.

modul vagy hosszú vektort az azt meghatározó irányított szakasz hosszának nevezzük. Jelölve || vagy ||.

Az úgynevezett nulla vektort, amelynek eleje és vége egybeesik, vektoroknak is nevezzük. Meg van jelölve. A nulla vektornak nincs határozott iránya, modulusa pedig nulla ||=0.

Vektorok és hívják kollineáris ha ugyanazon vagy párhuzamos vonalakon helyezkednek el. Ebben az esetben, ha a és vektorok egyforma irányúak, akkor ellentétesen írjuk a -t.

Az azonos síkkal párhuzamos egyeneseken elhelyezkedő vektorokat nevezzük egysíkú.

Két vektort és hívjuk egyenlő ha kollineárisak, azonos irányúak és egyenlő hosszúak. Ebben az esetben írjon.

A vektorok egyenlőségének definíciójából következik, hogy egy vektor önmagával párhuzamosan mozgatható, ha origóját a tér bármely pontjára helyezzük.

Például.

LINEÁRIS MŰVELETEK VEKTOROKRA

1. Egy vektor szorzata egy számmal.

   Egy vektor λ számmal való szorzata egy új vektor, amely:

   Egy vektor és egy λ szám szorzatát jelöljük.

   

   Például, olyan vektor, amely a vektorral azonos irányba mutat, és hossza fele a vektornak.

   A beírt művelet a következőkkel rendelkezik tulajdonságait:

2. Vektorok összeadása.

   Legyen és két tetszőleges vektor. Vegyünk egy tetszőleges pontot Oés készítsünk egy vektort. Ezek után a lényegtől A tedd félre a vektort. Az első vektor elejét a második végével összekötő vektort nevezzük összeg ezen vektorok közül, és jelöljük .

   

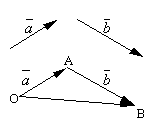
   A vektorösszeadás megfogalmazott definícióját ún paralelogramma szabály, mivel ugyanazt a vektorösszeget a következőképpen kaphatjuk meg. Tedd félre a ponttól O vektorok és . Szerkesszünk paralelogrammát ezekre a vektorokra! OABC. Mivel a vektorok , akkor a vektor , amely a csúcsból húzott paralelogramma átlója O, nyilvánvalóan a vektorok összege lesz.

   

   Könnyű ellenőrizni a következőket vektor összeadás tulajdonságai.

3. A vektorok különbsége.

   Egy adott vektorral kollineáris, egyenlő hosszúságú és ellentétes irányú vektort nevezünk szemben vektor egy vektorhoz, és jelöli. Az ellentétes vektort a λ = –1 számmal való vektorszorzás eredményének tekinthetjük: .

A négyzetes mátrix sajátvektora az, amelyet egy adott mátrixszal megszorozva kollineáris vektort kapunk. Egyszerű szavakkal, ha egy mátrixot megszorozunk egy sajátvektorral, az utóbbi ugyanaz marad, de megszorozzuk valamilyen számmal.

Meghatározás

A sajátvektor egy nem nulla V vektor, amely egy M négyzetmátrixszal megszorozva önmaga lesz, megnövelve valamilyen λ számmal. Algebrai jelölésben ez így néz ki:

M × V = λ × V,

ahol λ az M mátrix sajátértéke.

Nézzünk egy numerikus példát. Az írás megkönnyítése érdekében a mátrixban szereplő számokat pontosvessző választja el egymástól. Tegyük fel, hogy van egy mátrixunk:

• M=0; négy;
• 6; 10.

Szorozzuk meg egy oszlopvektorral:

• V = -2;

Ha egy mátrixot megszorozunk egy oszlopvektorral, akkor egy oszlopvektort is kapunk. Szigorú matematikai nyelven a 2 × 2-es mátrix oszlopvektorral való szorzásának képlete a következőképpen nézne ki:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

Az M11 az M mátrix első sorban és első oszlopában lévő elemét jelenti, M22 pedig a második sorban és a második oszlopban található elemet. A mi mátrixunknál ezek az elemek M11 = 0, M12 = 4, M21 = 6, M22 10. Oszlopvektor esetén ezek az értékek V11 = –2, V21 = 1. E képlet szerint a következőt kapjuk négyzetmátrix vektorral való szorzatának eredménye:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

A kényelem kedvéért az oszlopvektort egy sorba írjuk. Tehát a négyzetmátrixot megszoroztuk a (-2; 1) vektorral, így a (4; -2) vektort kaptuk. Nyilvánvaló, hogy ez ugyanaz a vektor, megszorozva λ = -2-vel. A lambda ebben az esetben a mátrix egy sajátértékét jelöli.

A mátrix sajátvektora egy kollineáris vektor, vagyis egy olyan objektum, amely nem változtatja meg a térbeli helyzetét, ha mátrixszal megszorozzuk. A vektoralgebrában a kollinearitás fogalma hasonló a geometriai párhuzamosság fogalmához. A geometriai értelmezésben a kollineáris vektorok párhuzamosan irányított, különböző hosszúságú szakaszok. Eukleidész kora óta tudjuk, hogy egyetlen egyenesnek végtelen számú vele párhuzamos egyenese van, ezért logikus azt feltételezni, hogy minden mátrix végtelen számú sajátvektorral rendelkezik.

Az előző példából látható, hogy mind a (-8; 4), mind a (16; -8), mind a (32, -16) lehet sajátvektor. Mindezek kollineáris vektorok, amelyek megfelelnek a λ = -2 sajátértéknek. Ha az eredeti mátrixot megszorozzuk ezekkel a vektorokkal, akkor is egy olyan vektort kapunk, amely 2-szer tér el az eredetitől. Éppen ezért a sajátvektor keresési feladatainak megoldása során csak lineárisan független vektorobjektumokat kell megtalálni. Leggyakrabban egy n × n mátrixhoz n-edik számú sajátvektor van. Számológépünk másodrendű négyzetmátrixok elemzésére készült, így szinte mindig két sajátvektor fog megjelenni, kivéve, ha azok egybeesnek.

A fenti példában előre tudtuk az eredeti mátrix sajátvektorát, és vizuálisan meghatároztuk a lambda számot. A gyakorlatban azonban minden fordítva történik: az elején sajátértékek vannak, és csak azután sajátvektorok.

Megoldási algoritmus

Nézzük meg újra az eredeti M mátrixot, és próbáljuk meg megtalálni mindkét sajátvektorát. Tehát a mátrix így néz ki:

• M=0; négy;
• 6; 10.

Először meg kell határoznunk a λ sajátértéket, amelyhez ki kell számítanunk a következő mátrix determinánsát:

• (0 − λ); négy;
• 6; (10 − λ).

Ezt a mátrixot úgy kapjuk meg, hogy kivonjuk az ismeretlen λ-t a főátlón lévő elemekből. A determinánst a standard képlet határozza meg:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Mivel a vektorunk nem lehet nulla, a kapott egyenletet lineárisan függőnek tekintjük, és a detA determinánsunkat nullával egyenlővé tesszük.

(0 − λ) × (10 − λ) − 24 = 0

Nyissuk ki a zárójeleket és kapjuk meg a mátrix karakterisztikus egyenletét:

λ 2 − 10λ − 24 = 0

Ez egy szabványos másodfokú egyenlet, amelyet a diszkrimináns szempontjából kell megoldani.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 = 100 + 96 \u003d 196

A diszkrimináns gyöke sqrt(D) = 14, tehát λ1 = -2, λ2 = 12. Most minden lambda értékhez meg kell találnunk egy sajátvektort. Adjuk meg a rendszer együtthatóit λ = -2 esetén.

• M − λ × E = 2; négy;
• 6; 12.

Ebben a képletben E az azonosságmátrix. A kapott mátrix alapján lineáris egyenletrendszert állítunk össze:

2x + 4y = 6x + 12y

ahol x és y a sajátvektor elemei.

Gyűjtsük össze az összes X-et a bal oldalon és az összes Y-t a jobb oldalon. Nyilvánvalóan - 4x = 8 év. Osszuk el a kifejezést -4-gyel, és kapjuk x = -2y. Most meghatározhatjuk a mátrix első sajátvektorát az ismeretlenek tetszőleges értékével (emlékezzünk a lineárisan függő sajátvektorok végtelenjére). Tegyük fel, hogy y = 1, majd x = -2. Ezért az első sajátvektor így néz ki: V1 = (–2; 1). Vissza a cikk elejére. Ezzel a vektorobjektummal szoroztuk meg a mátrixot, hogy bemutassuk a sajátvektor fogalmát.

Most keressük meg a λ = 12 sajátvektorát.

• M - λ × E = -12; négy
• 6; -2.

Állítsuk össze ugyanazt a lineáris egyenletrendszert;

• -12x + 4y = 6x - 2y
• -18x = -6 év
• 3x=y.

Most vegyük x = 1, tehát y = 3. Így a második sajátvektor így néz ki, mint V2 = (1; 3). Ha az eredeti mátrixot megszorozzuk ezzel a vektorral, az eredmény mindig ugyanaz a vektor lesz szorozva 12-vel. Ezzel befejeződik a megoldási algoritmus. Most már tudja, hogyan kell manuálisan meghatározni egy mátrix sajátvektorát.

• döntő;
• trace, azaz a főátlón lévő elemek összege;
• rang, azaz a lineárisan független sorok/oszlopok maximális száma.

A program a fenti algoritmus szerint működik, minimalizálva a megoldási folyamatot. Fontos kiemelni, hogy a programban a lambdát "c" betű jelöli. Nézzünk egy numerikus példát.

Program példa

Próbáljunk meg sajátvektorokat definiálni a következő mátrixhoz:

• M=5; 13;
• 4; 14.

Írjuk be ezeket az értékeket a számológép celláiba, és kapjuk meg a választ a következő formában:

• Mátrix rang: 2;
• Mátrix determináns: 18;
• Mátrix nyom: 19;
• Sajátvektor számítás: c 2 − 19.00c + 18.00 (karakteregyenlet);
• Sajátvektor számítás: 18 (első lambda érték);
• Sajátvektor számítás: 1 (második lambda érték);
• Az 1. vektor egyenletrendszere: -13x1 + 13y1 = 4x1 − 4y1;
• 2. vektor egyenletrendszer: 4x1 + 13y1 = 4x1 + 13y1;
• 1. sajátvektor: (1; 1);
• 2. sajátvektor: (-3,25; 1).

Így két lineárisan független sajátvektort kaptunk.

Következtetés

A lineáris algebra és az analitikus geometria alaptantárgyak minden pályakezdő mérnök számára. A vektorok és mátrixok nagy száma ijesztő, és ilyen nehézkes számítások során könnyű hibázni. Programunk lehetővé teszi a diákok számára, hogy ellenőrizzék számításaikat, vagy automatikusan megoldják a sajátvektor megtalálásának problémáját. Katalógusunkban további lineáris algebrai számológépek találhatók, használja őket tanulmányaiban vagy munkájában.

Meghatározás 9.3. Vektor x hívott saját vektor mátrixok DE ha van ilyen szám λ, hogy az egyenlőség fennáll: DE x= λ x, vagyis az arra való jelentkezés eredménye x mátrix által adott lineáris transzformáció DE, ennek a vektornak a szorzata a számmal λ . Maga a szám λ hívott saját szám mátrixok DE.

Behelyettesítés képletekre (9.3) x` j = λx j , egyenletrendszert kapunk a sajátvektor koordinátáinak meghatározására:

. (9.5)

Ennek a lineáris homogén rendszernek csak akkor lesz nem triviális megoldása, ha fő determinánsa 0 (Cramer-szabály). Ha ezt a feltételt a következő formában írja be:

egyenletet kapunk a sajátértékek meghatározására λ hívott karakterisztikus egyenlet. Röviden a következőképpen ábrázolható:

| A-λE | = 0, (9.6)

mivel bal oldala a mátrix meghatározója A-λE. Polinom viszonylatban λ | A-λE| hívott karakterisztikus polinom mátrixok a.

A karakterisztikus polinom tulajdonságai:

1) A lineáris transzformáció karakterisztikus polinomja nem függ a bázis megválasztásától. Bizonyíték. (lásd (9.4)), de Következésképpen, . Így nem függ az alap megválasztásától. Ezért és | A-λE| nem változik az új alapra való áttéréskor.

2) Ha a mátrix DE lineáris transzformáció az szimmetrikus(azok. a ij = a ji), akkor a (9.6) karakterisztikus egyenlet minden gyöke valós szám.

A sajátértékek és sajátvektorok tulajdonságai:

1) Ha sajátvektorok közül választunk bázist x 1, x 2, x 3 a sajátértékeknek megfelelő λ 1 , λ 2 , λ 3 mátrixok DE, akkor ezen az alapon az A lineáris transzformációnak van egy átlós mátrixa:

(9.7) Ennek a tulajdonságnak a bizonyítása a sajátvektorok definíciójából következik.

2) Ha a transzformáció sajátértékei DE különböznek, akkor a hozzájuk tartozó sajátvektorok lineárisan függetlenek.

3) Ha a mátrix karakterisztikus polinomja DE három különböző gyöke van, akkor valamilyen alapon a mátrix DEátlós alakja van.

Keressük meg a mátrix sajátértékeit és sajátvektorait. Készítsük el a karakterisztikus egyenletet: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Keresse meg az egyes talált értékekhez tartozó sajátvektorok koordinátáit! λ. A (9.5)-ből az következik, hogy ha x (1) ={x 1, x 2, x 3) a megfelelő sajátvektor λ 1 = -2 tehát

együttműködésen alapuló, de határozatlan rendszer. Megoldása így írható fel x (1) ={a,0,-a), ahol a tetszőleges szám. Különösen, ha szüksége van arra, hogy | x (1) |=1, x (1) =

Behelyettesítés a rendszerbe (9.5) λ 2 =3, kapunk egy rendszert a második sajátvektor koordinátáinak meghatározására - x (2) ={y1,y2,y3}:

, ahol x (2) ={b,-b,b) vagy feltéve, hogy | x (2) |=1, x (2) =

Mert λ 3 = 6 keresse meg a sajátvektort x (3) ={z1, z2, z3}:

, x (3) ={c,2c, c) vagy a normalizált változatban

x (3) = Ez látható x (1) x (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = időszámításunk előtt- 2bc + bc= 0. Így ennek a mátrixnak a sajátvektorai páronként ortogonálisak.

10. előadás

Másodfokú formák és kapcsolatuk szimmetrikus mátrixokkal. A szimmetrikus mátrix sajátvektorainak és sajátértékeinek tulajdonságai. Másodfokú forma redukálása kanonikus formává.

Meghatározás 10.1.másodfokú forma valós változók x 1, x 2,…, x n egy másodfokú polinomot nevezünk ezekre a változókra vonatkozóan, amely nem tartalmaz szabad tagot és elsőfokú tagokat.

Példák másodfokú alakzatokra:

(n = 2),

(n = 3). (10.1)

Emlékezzünk vissza a szimmetrikus mátrix utolsó előadásban adott definíciójára:

Meghatározás 10.2. A négyzetmátrixot ún szimmetrikus, ha , vagyis ha a főátlóhoz képest szimmetrikus mátrixelemek egyenlőek.

A szimmetrikus mátrix sajátértékeinek és sajátvektorainak tulajdonságai:

1) A szimmetrikus mátrix minden sajátértéke valós.

Bizonyíték (azért n = 2).

Hagyja a mátrixot DEúgy néz ki, mint a: . Készítsük el a karakterisztikus egyenletet:

(10.2) Keresse meg a diszkriminánst:

Ezért az egyenletnek csak valódi gyökerei vannak.

2) A szimmetrikus mátrix sajátvektorai ortogonálisak.

Bizonyíték (azért n= 2).

A és a sajátvektorok koordinátáinak meg kell felelniük az egyenleteknek.