Hogyan számítsuk ki a paralelepipedon területét. Különböző piramisok oldalsó felülete

A matematika vizsgára való felkészülés során a tanulóknak rendszerezniük kell algebrai és geometriai ismereteiket. Szeretnék az összes ismert információt egyesíteni, például a piramis területének kiszámítását. Sőt, az alap- és oldalfelülettől kezdve a teljes felületig. Ha az oldallapokkal egyértelmű a helyzet, mivel ezek háromszögek, akkor az alap mindig más.

Mi a teendő, ha megtalálja a piramis alapterületét?

Teljesen bármilyen alak lehet: tetszőleges háromszögtől egy n-szögig. Ez az alap pedig a szögek számának különbségén kívül lehet szabályos vagy hibás ábra. Az iskolások érdeklődésére számot tartó USE feladatokban csak a helyes számjegyekkel ellátott feladatok vannak az alján. Ezért csak róluk fogunk beszélni.

derékszögű háromszög

Ez egyenlő oldalú. Olyan, amelyben minden oldal egyenlő, és "a" betűvel jelöljük. Ebben az esetben a piramis alapterületét a következő képlettel számítjuk ki:

S = (a 2 * √3) / 4.

Négyzet

A terület kiszámításának képlete a legegyszerűbb, itt az "a" ismét az oldal:

Önkényes szabályos n-gon

A sokszög oldalának ugyanaz a jelölése. A sarkok számánál a latin n betűt használjuk.

S = (n * a 2) / (4 * tg (180º/n)).

Hogyan kell eljárni az oldalsó és a teljes felület kiszámításakor?

Mivel az alap egy szabályos alak, a piramis minden lapja egyenlő. Ráadásul mindegyik egyenlő szárú háromszög, mivel az oldalélek egyenlőek. Ezután a piramis oldalsó területének kiszámításához szükség van egy képletre, amely azonos monomok összegéből áll. A tagok számát az alap oldalainak száma határozza meg.

Az egyenlő szárú háromszög területét az a képlet számítja ki, amelyben az alap szorzatának felét megszorozzuk a magassággal. Ezt a magasságot a piramisban apotémnek nevezik. Megjelölése "A". Az oldalsó felület általános képlete a következő:

S \u003d ½ P * A, ahol P a piramis alapjának kerülete.

Vannak olyan helyzetek, amikor az alap oldalai nem ismertek, de az oldalélek (c) és a csúcsánál lévő lapos szög (α) adottak. Ezután egy ilyen képletet kell használni a piramis oldalsó területének kiszámításához:

S = n/2 * 2 sin α-ban .

1. feladat

Állapot. Határozza meg a piramis teljes területét, ha az alapja 4 cm-es oldallal esik, és az apotém értéke √3 cm.

Megoldás. Az alap kerületének kiszámításával kell kezdenie. Mivel ez egy szabályos háromszög, akkor P \u003d 3 * 4 \u003d 12 cm. Mivel az apotém ismert, azonnal kiszámíthatja a teljes oldalfelület területét: ½ * 12 * √3 = 6 √3 cm2.

Az alapnál lévő háromszög esetében a következő területértéket kapjuk: (4 2 * √3) / 4 \u003d 4√3 cm 2.

A teljes terület meghatározásához össze kell adnia a kapott két értéket: 6√3 + 4√3 = 10√3 cm 2.

Válasz. 10√3 cm2.

2. feladat

Állapot. Van egy szabályos négyszög alakú piramis. Az alap oldalának hossza 7 mm, oldaléle 16 mm. Ismernie kell a felületét.

Megoldás. Mivel a poliéder négyszögletes és szabályos, így alapja négyzet. Miután megtanulta az alap- és oldalfelületek területét, kiszámítható a piramis területe. A négyzet képlete fent található. Az oldallapoknál pedig a háromszög minden oldala ismert. Ezért használhatja Heron képletét a területük kiszámításához.

Az első számítások egyszerűek, és ehhez a számhoz vezetnek: 49 mm 2. A második értékhez ki kell számítania a fél kerületet: (7 + 16 * 2): 2 = 19,5 mm. Most kiszámolhatja egy egyenlő szárú háromszög területét: √ (19,5 * (19,5-7) * (19,5-16) 2) = √2985,9375 = 54,644 mm 2. Csak négy ilyen háromszög van, így a végső szám kiszámításakor meg kell szoroznia 4-gyel.

Kiderült: 49 + 4 * 54,644 \u003d 267,576 mm 2.

Válasz. A kívánt érték 267,576 mm2.

3. feladat

Állapot. Egy szabályos négyszög alakú piramis esetében ki kell számítani a területet. Ebben a négyzet oldala 6 cm, magassága 4 cm.

Megoldás. A képlet legegyszerűbb módja a kerület és az apotém szorzatával való felhasználás. Az első értéket könnyű megtalálni. A második egy kicsit nehezebb.

Emlékeznünk kell a Pitagorasz-tételre, és figyelembe kell venni, hogy azt a piramis magassága és az apotém, amely a hipotenusz alkotja. A második láb egyenlő a négyzet oldalának felével, mivel a poliéder magassága a közepébe esik.

A kívánt apotém (egy derékszögű háromszög befogója) √(3 2 + 4 2) = 5 (cm).

Most kiszámíthatja a kívánt értéket: ½ * (4 * 6) * 5 + 6 2 \u003d 96 (cm 2).

Válasz. 96 cm2.

4. feladat

Állapot. Alapjának megfelelő oldala 22 mm, oldalbordái 61 mm. Mekkora ennek a poliédernek az oldalfelülete?

Megoldás. A benne lévő indoklás megegyezik a 2. számú feladatnál leírtakkal. Csak ott kapott egy piramist, amelynek alapja négyzet, és most egy hatszög.

Először is, az alap területét a fenti képlettel számítjuk ki: (6 * 22 2) / (4 * tg (180º / 6)) \u003d 726 / (tg30º) \u003d 726√3 cm 2.

Most meg kell találnia egy egyenlő szárú háromszög fél kerületét, amely egy oldallap. (22 + 61 * 2): 2 = 72 cm. A Heron képlet segítségével ki kell számítani egy ilyen háromszög területét, majd megszorozni hattal, és hozzá kell adni ahhoz, amelyik kiderült bázis.

Számítások a Heron képlet segítségével: √ (72 * (72-22) * (72-61) 2) \u003d √ 435600 \u003d 660 cm 2. Az oldalfelületet megadó számítások: 660 * 6 = 3960 cm 2. A teljes felület kiderítéséhez össze kell adni őket: 5217,47≈5217 cm 2.

Válasz. Alap - 726√3 cm 2, oldalfelület - 3960 cm 2, teljes terület - 5217 cm 2.

A henger egy hengeres felületből és két párhuzamosan elhelyezett körből álló figura. A henger területének kiszámítása a matematika geometriai ágának problémája, amelyet meglehetősen egyszerűen megoldanak. Számos módszer létezik a megoldására, amelyek ennek eredményeként mindig egy képletre vezetnek le.

Hogyan lehet megtalálni a henger területét - számítási szabályok

• A henger területének meghatározásához hozzá kell adni két alapterületet az oldalfelület területével: S \u003d S oldal. + 2 S fő. Egy részletesebb változatban ez a képlet így néz ki: S= 2 π rh+ 2 π r2= 2 π r(h+ r).
• Egy adott geometriai test oldalfelülete akkor számítható ki, ha ismert a magassága és az alapja alatti kör sugara. Ebben az esetben megadhatja a kerület sugarát, ha az adott. A magasság akkor található meg, ha a generatrix értéke a feltételben meg van adva. Ebben az esetben a generatrix egyenlő lesz a magassággal. Egy adott test oldalfelületének képlete a következőképpen néz ki: S= 2 π rh.
• Az alap területét a kör területének meghatározására szolgáló képlet számítja ki: S osn= π r 2 . Egyes feladatokban előfordulhat, hogy a sugár nincs megadva, de a kerület adott. Ezzel a képlettel a sugár meglehetősen könnyen kifejezhető. С=2π r, r= С/2π. Emlékeztetni kell arra is, hogy a sugár az átmérő fele.
• Mindezen számítások végrehajtásakor a π számot általában nem fordítják le 3,14159-re ... Csak hozzá kell adni a számítások eredményeként kapott számérték mellé.
• Továbbá csak az alap talált területét kell megszorozni 2-vel, és a kapott számhoz hozzá kell adni az ábra oldalfelületének számított területét.
• Ha a probléma azt jelzi, hogy a hengernek tengelyirányú metszete van, és ez egy téglalap, akkor a megoldás kissé eltérő lesz. Ebben az esetben a téglalap szélessége a test alján fekvő kör átmérője lesz. Az ábra hossza megegyezik a generatrix vagy a henger magasságával. Ki kell számítani a kívánt értékeket, és helyettesíteni kell egy már ismert képlettel. Ebben az esetben a téglalap szélességét el kell osztani kettővel, hogy megtaláljuk az alap területét. Az oldalfelület meghatározásához a hosszt meg kell szorozni két sugárral és a π számmal.
• Egy adott geometriai test területét a térfogatán keresztül számíthatja ki. Ehhez le kell vezetni a hiányzó értéket a V=π r 2 h képletből.
• A henger területének kiszámításában nincs semmi nehéz. Csak a képleteket kell ismerni és belőlük levezetni a számításokhoz szükséges mennyiségeket.

A piramis felülete. Ebben a cikkben megvizsgáljuk a normál piramisokkal kapcsolatos problémákat. Hadd emlékeztesselek arra, hogy a szabályos piramis olyan gúla, amelynek alapja egy szabályos sokszög, a piramis csúcsa ennek a sokszögnek a közepébe vetül.

Egy ilyen piramis oldallapja egyenlő szárú háromszög.Ennek a háromszögnek a magasságát, amelyet egy szabályos piramis tetejéről húzunk, apotémának nevezzük, az SF pedig apotémát:

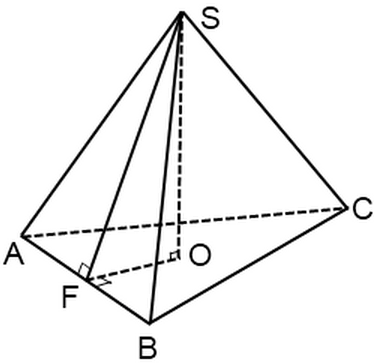
Az alábbiakban bemutatott típusú problémáknál meg kell találni a teljes piramis felületét vagy oldalsó felületének területét. A blog már több problémával foglalkozott a szabályos piramisokkal kapcsolatban, ahol felmerült az elemek megtalálása (magasság, alapél, oldalél), .

A vizsga feladataiban általában szabályos három-, négy- és hatszögletű piramisokat vesznek figyelembe. Nem láttam problémát a szabályos ötszögletű és hétszögletű piramisoknál.

A teljes felület területének képlete egyszerű - meg kell találnia a piramis alapterületének és oldalsó felületének területének összegét:

Fontolja meg a feladatokat:

Egy szabályos négyszög alakú gúla alapjának oldalai 72, oldalélei 164. Határozzuk meg ennek a gúlának a felületét!

A piramis felülete megegyezik az oldalfelület és az alap területeinek összegével:

*Az oldalfelület négy egyenlő területű háromszögből áll. A piramis alapja egy négyzet.

A piramis oldalának területe a következőképpen számítható ki:

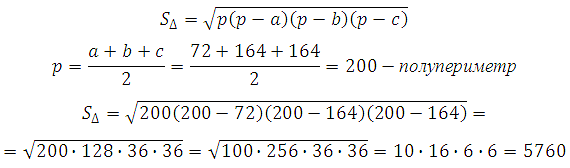
Így a piramis felülete:

Válasz: 28224

Egy szabályos hatszögletű gúla alapjának oldalai 22, oldalélei 61. Határozzuk meg ennek a gúlának az oldalfelületének területét!

A szabályos hatszögletű piramis alapja egy szabályos hatszög.

Ennek a piramisnak az oldalfelülete hat egyenlő háromszög területéből áll, amelyek oldala 61,61 és 22:

Keresse meg a háromszög területét Heron képletével:

Tehát az oldalsó felület:

Válasz: 3240

*A fent bemutatott feladatokban az oldallap területét egy másik háromszögképlet segítségével lehetett megtalálni, de ehhez ki kell számítani az apotémet.

27155. Határozza meg egy szabályos négyszög alakú gúla felületét, amelynek alapoldalai 6, magassága 4!

A piramis felületének meghatározásához ismernünk kell az alap és az oldalfelület területét:

Az alap területe 36, mivel ez egy négyzet, amelynek oldala 6.

Az oldalfelület négy lapból áll, amelyek egyenlő háromszögek. Egy ilyen háromszög területének megtalálásához ismernie kell az alapját és magasságát (apotém):

* Egy háromszög területe egyenlő az alap és az ehhez az alaphoz húzott magasság szorzatának felével.

Az alap ismert, egyenlő hattal. Keressük a magasságot. Tekintsünk egy derékszögű háromszöget (sárgával kiemelve):

Az egyik láb egyenlő 4-gyel, mivel ez a piramis magassága, a másik egyenlő 3-mal, mivel egyenlő az alap szélének felével. A hipotenuszt a Pitagorasz-tétel segítségével találhatjuk meg:

Tehát a piramis oldalfelületének területe:

Így a teljes piramis felülete:

Válasz: 96

27069. Egy szabályos négyszög alakú gúla alapjának oldalai 10, oldalélei 13. Határozzuk meg ennek a gúlának a felületét!

27070. Egy szabályos hatszögletű gúla alapjának oldalai 10, oldalélei 13. Határozzuk meg ennek a gúlának az oldalfelületének területét!

Vannak képletek a szabályos piramis oldalfelületére is. Egy szabályos piramisban az alap az oldalfelület merőleges vetülete, ezért:

P- az alap kerülete, l- a piramis apotémája

*Ez a képlet egy háromszög területének képletén alapul.

Ha többet szeretne megtudni e képletek származtatásáról, ne hagyja ki, kövesse a cikkek megjelenését.Ez minden. Sok szerencsét!

Üdvözlettel: Alexander Krutitskikh.

P.S. Hálás lennék, ha a közösségi oldalakon mesélne az oldalról.

A henger egy geometriai test, amelyet két párhuzamos sík és egy hengeres felület határol. A cikkben arról fogunk beszélni, hogyan lehet megtalálni a henger területét, és a képlet segítségével például számos problémát megoldunk.

A hengernek három felülete van: egy felső, egy alsó és egy oldalfelület.

A henger teteje és alja kör alakú, és könnyen azonosítható.

Ismeretes, hogy egy kör területe egyenlő πr 2 -vel. Ezért a két kör (a henger teteje és alja) területének képlete így fog kinézni: πr 2 + πr 2 = 2πr 2.

A henger harmadik, oldalfelülete a henger ívelt fala. Ennek a felületnek a jobb ábrázolása érdekében próbáljuk meg átalakítani, hogy felismerhető formát kapjunk. Képzelje el, hogy a henger egy közönséges konzervdoboz, amelynek nincs felső fedele és alja. Vegyünk egy függőleges bevágást az oldalfalon az üveg tetejétől az aljáig (1. lépés az ábrán), és próbáljuk meg a kapott figurát minél jobban kinyitni (kiegyenesíteni) (2. lépés).

A kapott tégely teljes nyilvánosságra hozatala után egy ismerős alakot fogunk látni (3. lépés), ez egy téglalap. A téglalap területe könnyen kiszámítható. De előtte térjünk vissza egy pillanatra az eredeti hengerhez. Az eredeti henger csúcsa egy kör, és tudjuk, hogy a kör kerületét a következő képlettel számítjuk ki: L = 2πr. Az ábrán pirossal van jelölve.

Amikor a henger oldalfala teljesen kitágult, azt látjuk, hogy a kerülete a kapott téglalap hosszává válik. Ennek a téglalapnak az oldalai a henger kerülete (L = 2πr) és magassága (h). A téglalap területe egyenlő az oldalai szorzatával - S = hosszúság x szélesség = L x h = 2πr x h = 2πrh. Ennek eredményeként egy képletet kaptunk a henger oldalfelületének kiszámítására.

A henger oldalfelületének területének képlete
S oldal = 2prh

A henger teljes felülete

Végül, ha mindhárom felület területét összeadjuk, megkapjuk a henger teljes felületének képletét. A henger felülete megegyezik a henger tetejének területével + a henger aljának területével + a henger oldalfelületének területével vagy S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Néha ezt a kifejezést az azonos 2πr (r + h) képlettel írják le.

A henger teljes felületének képlete
S = 2πr 2 + 2πrh = 2πr(r + h)
r a henger sugara, h a henger magassága

Példák egy henger felületének kiszámítására

A fenti képletek megértéséhez próbáljuk meg kiszámítani egy henger felületét példák segítségével.

1. A henger alapjának sugara 2, magassága 3. Határozza meg a henger oldalfelületének területét.

A teljes felületet a következő képlettel számítjuk ki: S oldal. = 2prh

S oldal = 2*3,14*2*3

S oldal = 6,28 * 6

S oldal = 37,68

A henger oldalfelülete 37,68.

2. Hogyan találjuk meg egy henger felületét, ha a magassága 4, a sugara pedig 6?

A teljes felületet a következő képlettel számítjuk ki: S = 2πr 2 + 2πrh

S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

- Ez egy poliéder alak, amelynek alapjában egy sokszög található, a fennmaradó lapokat pedig közös csúcsú háromszögek ábrázolják.

Ha az alap négyzet, akkor piramist nevezünk négyszögű, ha a háromszög az háromszög alakú. A piramis magasságát a tetejétől merőlegesen az alapra húzzuk. A terület kiszámításához is használják apotém az oldallap magassága a csúcsától leeresztve.
A piramis oldalfelületének területének képlete az egymással egyenlő oldallapok területének összege. Ezt a számítási módszert azonban nagyon ritkán használják. Alapvetően a piramis területét az alap és az apotém kerületén keresztül számítják ki:

Vegyünk egy példát a piramis oldalsó felületének kiszámítására.

Legyen adott egy ABCDE bázisú és F csúcsú gúla. AB =BC =CD =DE =EA =3 cm. Apotém a = 5 cm. Határozza meg a gúla oldalfelületének területét!
Keressük a kerületet. Mivel az alap minden lapja egyenlő, akkor az ötszög kerülete egyenlő lesz:
Most megtalálhatja a piramis oldalsó területét:

Egy szabályos háromszög alakú piramis területe

A szabályos háromszög alakú gúla egy alapból, amelyben egy szabályos háromszög fekszik, és három oldallapból áll, amelyek területe egyenlő.
A szabályos háromszög alakú piramis oldalfelületének képlete sokféleképpen kiszámítható. Alkalmazhatja a szokásos képletet a kerületen és az apotémon keresztül történő kiszámításához, vagy megkeresheti az egyik arc területét, és megszorozhatja hárommal. Mivel a piramis lapja háromszög, a képletet a háromszög területére alkalmazzuk. Szükség lesz egy apotémra és az alap hosszára. Vegyünk egy példát egy szabályos háromszög alakú piramis oldalfelületének kiszámítására.

Adott egy gúla, amelynek apotémje a = 4 cm és alaplapja b = 2 cm. Határozza meg a gúla oldalfelületének területét!
Először keresse meg az egyik oldalfelület területét. Ebben az esetben ez lesz:
Cserélje be az értékeket a képletben:
Mivel egy szabályos piramisban minden oldal azonos, a piramis oldalfelületének területe egyenlő lesz a három lap területének összegével. Illetőleg:

A csonka piramis területe

Megcsonkított A piramis olyan poliéder, amelyet egy gúla alkot, és annak alappal párhuzamos szakasza.
A csonka piramis oldalfelületének képlete nagyon egyszerű. A terület egyenlő az alapok kerülete és az apotém összegének felének szorzatával: