valor natural. Números naturales - conceptos básicos

Los números son un concepto abstracto. Son una característica cuantitativa de los objetos y son reales, racionales, negativos, enteros y fraccionarios, así como naturales.

La serie natural se usa generalmente en el conteo, en el que surgen naturalmente las designaciones de cantidad. El conocimiento de la cuenta comienza en la primera infancia. ¿Qué niño ha evitado las rimas de conteo divertidas, en las que solo se usaron elementos de conteo natural? “Uno, dos, tres, cuatro, cinco… ¡El conejito salió a caminar!” o "1, 2, 3, 4, 5, 6, 7, 8, 9, 10, el rey decidió ahorcarme..."

Para cualquier número natural, puedes encontrar otro, mayor que él. Este conjunto generalmente se denota con la letra N y debe considerarse infinito en la dirección del aumento. Pero este conjunto tiene un comienzo: esta es una unidad. Aunque existen números naturales franceses, cuyo conjunto también incluye el cero. Pero la principal característica distintiva de ambos conjuntos es el hecho de que no incluyen números fraccionarios ni negativos.

La necesidad de contar una variedad de artículos surgió en tiempos prehistóricos. Entonces supuestamente se formó el concepto de "números naturales". Su formación tuvo lugar a lo largo de todo el proceso de cambio de la cosmovisión de una persona, el desarrollo de la ciencia y la tecnología.

Sin embargo, todavía no podían pensar en abstracto. Les resultó difícil entender cuál es el carácter común de los conceptos de "tres cazadores" o "tres árboles". Por lo tanto, al indicar el número de personas, se utilizó una definición, y al indicar el mismo número de objetos de diferente tipo, se utilizó una definición completamente diferente.

Y fue extremadamente corto. En él solo estaban presentes los números 1 y 2, y la cuenta finalizaba con el concepto de “muchos”, “rebaño”, “multitud”, “montón”.

Posteriormente se formó una cuenta más progresista, ya más amplia. Un hecho interesante es que solo había dos números: 1 y 2, y los siguientes números ya se obtuvieron sumando.

Un ejemplo de esto fue la información que nos ha llegado sobre la serie de números de la tribu australiana. Ellos 1 denotaron la palabra "Enza" y 2 - la palabra "petcheval". Por lo tanto, el número 3 sonaba como "petcheval-Enza", y el 4, ya como "petcheval-petcheval".

La mayoría de las naciones reconocieron los dedos como el estándar para contar. Además, el desarrollo del concepto abstracto de "números naturales" siguió el camino del uso de muescas en un palo. Y luego hubo la necesidad de designar una docena con otro signo. Los antiguos, a nuestra salida, comenzaron a usar otro palo, en el que se hicieron muescas, que indicaban las decenas.

Las posibilidades de reproducir números se expandieron enormemente con el advenimiento de la escritura. Al principio, los números se representaban como guiones en tablillas de arcilla o papiro, pero poco a poco comenzaron a usarse otros signos para escribir, así fue como aparecieron los números romanos.

Mucho más tarde apareció lo que abrió la posibilidad de escribir números con un conjunto de caracteres relativamente pequeño. Hoy no es difícil escribir números tan grandes como la distancia entre los planetas y el número de estrellas. Uno solo tiene que aprender a usar los grados.

Euclides en el siglo III aC en el libro "Principios" establece el infinito del conjunto numérico y Arquímedes en "Psamit" revela los principios para construir los nombres de números arbitrariamente grandes. Casi hasta mediados del siglo XIX, la gente no se enfrentó a la necesidad de una formulación clara del concepto de “números naturales”. La definición se requirió con el advenimiento del método matemático axiomático.

Y en los años 70 del siglo XIX formuló una definición clara de los números naturales basada en el concepto de conjunto. Y hoy ya sabemos que los números naturales son todos los números enteros, que van del 1 al infinito. Los niños pequeños, dando su primer paso para conocer a la reina de todas las ciencias, las matemáticas, comienzan a estudiar estos números.

1.1 Definición

Los números que la gente usa para contar se llaman natural(por ejemplo, uno, dos, tres, ..., cien, ciento uno, ..., tres mil doscientos veintiuno, ...) Para escribir números naturales, se utilizan signos especiales (símbolos) , llamado cifras.

Hoy en día aceptado notación decimal. El sistema decimal (o forma) de escribir números usa números arábigos. Estos son diez caracteres de dígitos diferentes: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 .

El menos un número natural es un número uno, eso escrito con un dígito decimal - 1. El siguiente número natural se obtiene del anterior (excepto uno) sumando 1 (uno). Esta suma se puede hacer muchas veces (un número infinito de veces). Esto significa que No mayor número natural. Por eso se dice que la serie de los números naturales es ilimitada o infinita, ya que no tiene fin. Los números naturales se escriben usando dígitos decimales.

1.2. El número "cero"

Para indicar la ausencia de algo, utilice el número " cero" o " cero". Se escribe con números. 0 (cero). Por ejemplo, en una caja todas las bolas son rojas. ¿Cuántos de ellos son verdes? - Respuesta: cero . ¡Entonces no hay bolas verdes en la caja! El número 0 puede significar que algo ha terminado. Por ejemplo, Masha tenía 3 manzanas. Compartió dos con amigos, uno se comió ella misma. Entonces ella se ha ido 0 (cero) manzanas, i.e. nadie. El número 0 podría significar que algo no sucedió. Por ejemplo, un partido de hockey entre el equipo ruso y el equipo canadiense terminó con el marcador 3:0 (léase "tres - cero") a favor del equipo ruso. Esto significa que el equipo ruso anotó 3 goles y el equipo canadiense 0 goles, no pudo marcar un solo gol. debemos recordar que el cero no es un número natural.

1.3. escribir numeros naturales

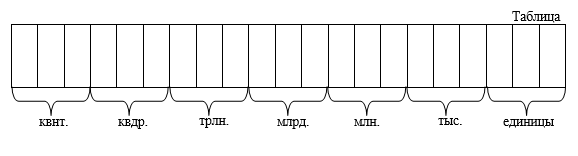
En la forma decimal de escribir un número natural, cada dígito puede significar números diferentes. Depende del lugar de este dígito en la notación del número. Un cierto lugar en la notación de un número natural se llama posición. Por lo tanto, la notación decimal se llama posicional Considere la notación decimal 7777 del número siete mil setecientos setenta y siete. Hay siete mil, setecientos, siete decenas y siete unidades en esta entrada.

Cada uno de los lugares (posiciones) en la notación decimal de un número se llama descargar. Cada tres dígitos se combinan en Clase. Esta unión se realiza de derecha a izquierda (desde el final de la entrada del número). Los diferentes rangos y clases tienen sus propios nombres. El número de números naturales es ilimitado. Por lo tanto, el número de rangos y clases tampoco está limitado ( infinitamente). Considere los nombres de dígitos y clases usando el ejemplo de un número con notación decimal

38 001 102 987 000 128 425:

Clases y rangos
quintillones		cientos de quintillones
		decenas de quintillones
		quintillones
cuatrillones		cientos de cuatrillones
		decenas de cuatrillones
		cuatrillones
trillones		cientos de billones
		decenas de billones
		trillones
miles de millones		cientos de miles de millones
		decenas de miles de millones
		miles de millones
millones		cientos de millones
		Decenas de millones
		millones
		cientos de miles
		Decenas de miles

Entonces, las clases, comenzando con la más joven, tienen nombres: unidades, miles, millones, billones, trillones, cuatrillones, quintillones.

1.4. Unidades de bits

Cada una de las clases en la notación de números naturales consta de tres dígitos. Cada rango tiene unidades de bits. Los siguientes números se denominan unidades de bits:

1 - dígito unidad de dígito de unidades,

10 - unidad de dígito del dígito de las decenas,

100 - unidad de bits del dígito de las centenas,

1 000 - unidad de bits del lugar de los millares,

10,000 - unidad de dígito de decenas de miles,

100,000 - unidad de bit de cientos de miles,

1,000,000 es la unidad de dígito del dígito de millones, etc.

El número en cualquiera de los dígitos muestra el número de unidades de este dígito. Entonces, el número 9, en el lugar de los cientos de miles de millones, significa que el número 38,001,102,987,000 128,425 incluye nueve mil millones (es decir, 9 veces 1,000,000,000 o 9 unidades de bits de los miles de millones). Un dígito vacío de centenas de quintillones significa que no hay centenas de quintillones en este número o que su número es igual a cero. En este caso, el número 38 001 102 987 000 128 425 se puede escribir de la siguiente manera: 038 001 102 987 000 128 425.

Puede escribirlo de otra manera: 000 038 001 102 987 000 128 425. Los ceros al comienzo del número indican dígitos vacíos de orden superior. Por lo general, no se escriben, a diferencia de los ceros dentro de la notación decimal, que necesariamente marcan dígitos vacíos. Entonces, tres ceros en la clase de millones significa que los dígitos de cientos de millones, decenas de millones y unidades de millones están vacíos.

1.5. Abreviaturas en la escritura de números.

Al escribir números naturales, se utilizan abreviaturas. Aquí hay unos ejemplos:

1,000 = 1 mil (mil)

23,000,000 = 23 millones (veintitrés millones)

5,000,000,000 = 5 mil millones (cinco mil millones)

203,000,000,000,000 = 203 billones (doscientos tres billones)

107.000.000.000.000.000 = 107 m2. (ciento siete cuatrillones)

1.000.000.000.000.000.000 = 1 kw. (un quintillón)

Bloque 1.1. Diccionario

Compile un glosario de nuevos términos y definiciones de §1. Para hacer esto, en las celdas vacías, ingrese las palabras de la lista de términos a continuación. En la tabla (al final del bloque), indique para cada definición el número del término de la lista.

Bloque 1.2. Auto-entrenamiento

En el mundo de los grandes números

Economía .

1. El presupuesto de Rusia para el próximo año será: 6328251684128 rublos.
2. Gastos previstos para este año: 5124983252134 rublos.
3. Los ingresos del país superaron los gastos en 1203268431094 rublos.

preguntas y tareas

1. Leer los tres números dados
2. Escriba los dígitos en la clase de millón de cada uno de los tres números

1. ¿Qué sección en cada uno de los números pertenece al dígito en la séptima posición desde el final de la notación de números?
2. ¿Qué número de unidades de bits muestra el número 2 en el primer número?... en el segundo y tercer número?
3. Nombre la unidad de bit para la octava posición desde el final en la notación de tres números.

Geografía (longitud)

1. Radio ecuatorial de la Tierra: 6378245 m
2. Circunferencia del ecuador: 40075696 m
3. La mayor profundidad del océano mundial (Fosa de Marian en el Océano Pacífico) 11500 m

preguntas y tareas

1. Convierte los tres valores a centímetros y lee los números resultantes.
2. Para el primer número (en cm), anote los números en las secciones:

cientos de miles _______

Decenas de millones _______

miles de _______

billones de _______

cientos de millones de _______

1. Para el segundo número (en cm), escriba las unidades de bits correspondientes a los números 4, 7, 5, 9 en la entrada de números

1. Convierta el tercer valor a milímetros, lea el número resultante.
2. Para todas las posiciones en el registro del tercer número (en mm), indique los dígitos y las unidades de dígitos en la tabla:

Geografía (cuadrado)

1. El área de toda la superficie de la Tierra es de 510.083 mil kilómetros cuadrados.
2. La superficie de las sumas en la Tierra es de 148.628 mil kilómetros cuadrados.
3. El área de la superficie del agua de la Tierra es de 361,455 mil kilómetros cuadrados.

preguntas y tareas

1. Convierte los tres valores a metros cuadrados y lee los números resultantes.
2. Nombre las clases y rangos correspondientes a dígitos distintos de cero en el registro de estos números (en metros cuadrados).
3. En la entrada del tercer número (en m2), nombre las unidades de bit correspondientes a los números 1, 3, 4, 6.
4. En dos entradas del segundo valor (en km2 y m2), indique a qué dígitos pertenece el número 2.
5. Escriba las unidades de bits para el número 2 en los registros del segundo valor.

Bloque 1.3. Diálogo con una computadora.

Se sabe que los números grandes se usan a menudo en astronomía. Demos ejemplos. La distancia media de la Luna a la Tierra es de 384 mil km. La distancia de la Tierra al Sol (promedio) es de 149504 mil km, la Tierra de Marte es de 55 millones de km. En una computadora, usando el editor de texto de Word, cree tablas para que cada dígito en el registro de los números indicados esté en una celda separada (celda). Para hacer esto, ejecute los comandos en la barra de herramientas: tabla → agregar tabla → número de filas (ponga "1" con el cursor) → número de columnas (calcule usted mismo). Cree tablas para otros números (bloque "Autopreparación").

Bloque 1.4. Relevo de grandes números

La primera fila de la tabla contiene un gran número. Léalo. Luego complete las tareas: moviendo los números en la entrada de números hacia la derecha o hacia la izquierda, obtenga los siguientes números y léalos. (¡No mueva los ceros al final del número!). En la clase, la batuta se puede llevar a cabo pasándosela unos a otros.

Línea 2 . Mueva todos los dígitos del número en la primera línea hacia la izquierda a través de dos celdas. Reemplace los números 5 con el número que le sigue. Rellene las celdas vacías con ceros. Lee el número.

Línea 3 . Mueva todos los dígitos del número en la segunda línea a la derecha a través de tres celdas. Reemplace los números 3 y 4 en la entrada de números con los siguientes números. Rellene las celdas vacías con ceros. Lee el número.

Línea 4. Mueva todos los dígitos del número en la línea 3 una celda a la izquierda. Cambie el número 6 en la clase de trillones al anterior, y en la clase de mil millones al siguiente número. Rellene las celdas vacías con ceros. Lee el número resultante.

Línea 5 . Mueva todos los dígitos del número en la línea 4 una celda a la derecha. Reemplace el número 7 en el lugar de las "decenas de miles" con el anterior, y en el lugar de las "decenas de millones" con el siguiente. Lee el número resultante.

Línea 6 . Mueva todos los dígitos del número en la línea 5 a la izquierda después de 3 celdas. Cambia el número 8 en el lugar de las centenas de miles de millones al anterior, y el número 6 en el lugar de las centenas de millones al siguiente número. Rellene las celdas vacías con ceros. Calcula el número resultante.

Línea 7 . Mueva todos los dígitos del número en la línea 6 a la derecha una celda. Intercambia los dígitos en decenas de cuatrillones y decenas de miles de millones de lugares. Lee el número resultante.

Línea 8 . Mueva todos los dígitos del número en la línea 7 a la izquierda a través de una celda. Intercambia los dígitos en los lugares de quintillones y cuatrillones. Rellene las celdas vacías con ceros. Lee el número resultante.

Línea 9 . Mueva todos los dígitos del número en la línea 8 a la derecha a través de tres celdas. Intercambia dos números adyacentes en la fila de números de las clases de millones y billones. Lee el número resultante.

línea 10 . Mueva todos los dígitos del número en la línea 9 una celda a la derecha. Lee el número resultante. Resalta los números que indican el año de la Olimpiada de Moscú.

Bloque 1.5. Vamos a jugar

Encender un fuego

El campo de juego es un dibujo de un árbol de Navidad. Tiene 24 bombillas. Pero solo 12 de ellos están conectados a la red eléctrica. Para seleccionar las lámparas conectadas, debe responder correctamente las preguntas con las palabras "Sí" o "No". El mismo juego se puede jugar en una computadora; la respuesta correcta “enciende” la bombilla.

1. ¿Es cierto que los números son signos especiales para escribir números naturales? (1 - sí, 2 - no)
2. ¿Es cierto que 0 es el número natural más pequeño? (3 - sí, 4 - no)
3. ¿Es cierto que en el sistema numérico posicional el mismo dígito puede denotar números diferentes? (5 - sí, 6 - no)
4. ¿Es cierto que cierto lugar en la notación decimal de los números se llama lugar? (7 - sí, 8 - no)
5. Dado el número 543 384. ¿Es cierto que el número de los dígitos más significativos es 543 y el más bajo 384? (9 - sí, 10 - no)
6. ¿Es cierto que en la clase de los billones, la unidad de bit más antigua es cien mil millones y la más joven es 1 billón? (11 - sí, 12 - no)
7. Se da el número 458 121. ¿Es cierto que la suma del número de los dígitos más significativos y el número de los menos significativos es 5? (13 - sí, 14 - no)
8. ¿Es cierto que la más antigua de las unidades de un billón de clases es un millón de veces más grande que la más antigua de las unidades de un millón de clases? (15 - sí, 16 - no)
9. Dados dos números 637508 y 831, ¿es cierto que el 1 más significativo del primer número es 1000 veces el 1 más significativo del segundo número? (17 - sí, 18 - no)
10. Se da el número 432. ¿Es cierto que la unidad de bits más significativa de este número es 2 veces mayor que la más joven? (19 - sí, 20 - no)
11. Dado el número 100.000.000, ¿es cierto que el número de unidades de bits que componen 10.000 en él es 1000? (21 - sí, 22 - no)
12. ¿Es cierto que la clase del billón está precedida por la clase del cuatrillón y que la clase del quintillón está precedida por esa clase? (23 - sí, 24 - no)

1.6. De la historia de los números.

Desde la antigüedad, el hombre se ha enfrentado a la necesidad de contar el número de cosas, de comparar el número de objetos (por ejemplo, cinco manzanas, siete flechas...; en una tribu hay 20 hombres y treinta mujeres,... .). También existía la necesidad de establecer un orden dentro de un cierto número de objetos. Por ejemplo, al cazar, el líder de la tribu va primero, el segundo es el guerrero más fuerte de la tribu, etc. Para estos fines, se utilizaron números. Se inventaron nombres especiales para ellos. En el habla, se les llama numerales: uno, dos, tres, etc. son números cardinales, y el primero, segundo, tercero son números ordinales. Los números se escribieron usando caracteres especiales: números.

Con el tiempo hubo sistemas numéricos. Estos son sistemas que incluyen formas de escribir números y varias acciones sobre ellos. Los sistemas numéricos más antiguos que se conocen son los sistemas numéricos egipcio, babilónico y romano. En Rus en los viejos tiempos, las letras del alfabeto con un signo especial ~ (título) se usaban para escribir números. El sistema numérico decimal es actualmente el más utilizado. Los sistemas numéricos binarios, octales y hexadecimales son muy utilizados, especialmente en el mundo de la informática.

Entonces, para escribir el mismo número, puede usar diferentes signos: números. Entonces, el número cuatrocientos veinticinco se puede escribir en números egipcios - jeroglíficos:

Esta es la forma egipcia de escribir números. El mismo número en números romanos: CDXXV(forma romana de escribir números) o dígitos decimales 425 (notación decimal de números). En notación binaria, se ve así: 110101001 (notación binaria o binaria de números), y en octal - 651 (notación octal de números). En notación hexadecimal, se escribirá: 1A9(notación hexadecimal). Puede hacerlo de manera muy simple: haga, como Robinson Crusoe, cuatrocientas veinticinco muescas (o trazos) en un poste de madera: IIIIIIIII…... tercero. Estas son las primeras imágenes de números naturales.

Entonces, en el sistema decimal de escribir números (en la forma decimal de escribir números), se usan números arábigos. Estos son diez caracteres diferentes - números: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 . En binario, dos dígitos binarios: 0, 1; en octal - ocho dígitos octales: 0, 1, 2, 3, 4, 5, 6, 7; en hexadecimal - dieciséis dígitos hexadecimales diferentes: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F; en sexagesimal (babilónico) - sesenta caracteres diferentes - números, etc.)

Los dígitos decimales llegaron a los países europeos desde el Medio Oriente, los países árabes. De ahí el nombre - números arábigos. Pero llegaron a los árabes desde la India, donde se inventaron a mediados del primer milenio.

1.7. sistema de numeración romana

Uno de los sistemas numéricos antiguos que se usa hoy en día es el sistema romano. Damos en la tabla los números principales del sistema de numeración romana y los números correspondientes del sistema decimal.

Números romanos					C
				50 cincuenta		500 quinientos	1000 mil

El sistema de numeración romana es sistema de adición En él, a diferencia de los sistemas posicionales (por ejemplo, decimal), cada dígito denota el mismo número. si, grabar Yo- denota el número dos (1 + 1 = 2), notación tercero- número tres (1 + 1 + 1 = 3), notación XXX- el número treinta (10 + 10 + 10 = 30), etc. Las siguientes reglas se aplican a la escritura de números.

1. si el numero menor es después más grande, entonces se suma a la más grande: VII- el número siete (5 + 2 = 5 + 1 + 1 = 7), XVII- número diecisiete (10 + 7 = 10 + 5 + 1 + 1 = 17), MCL- el número mil ciento cincuenta (1000 + 100 + 50 = 1150).
2. si el numero menor es antes mayor, entonces se resta de la mayor: IX- número nueve (9 = 10 - 1), LM- el número novecientos cincuenta (1000 - 50 = 950).

Para escribir números grandes, debe usar (inventar) nuevos caracteres: números. Al mismo tiempo, las entradas de números resultan engorrosas, es muy difícil realizar cálculos con números romanos. Entonces el año del lanzamiento del primer satélite terrestre artificial (1957) en notación romana tiene la forma MCMLVII .

Bloque 1. 8. Tarjeta perforada

Lectura de números naturales

Estas tareas se comprueban mediante un mapa con círculos. Expliquemos su aplicación. Después de completar todas las tareas y encontrar las respuestas correctas (están marcadas con las letras A, B, C, etc.), coloque una hoja de papel transparente en la tarjeta. Marque las respuestas correctas con marcas "X", así como la marca de combinación "+". Luego coloque la hoja transparente en la página para que las marcas de alineación coincidan. Si todas las marcas "X" están en los círculos grises en esta página, las tareas se completaron correctamente.

1.9. Orden de lectura de los números naturales

Al leer un número natural, proceda de la siguiente manera.

1. Descomponga mentalmente el número en triples (clases) de derecha a izquierda, desde el final de la entrada del número.

1. A partir de la clase junior, de derecha a izquierda (desde el final de la entrada del número), escriben los nombres de las clases: unidades, miles, millones, billones, trillones, cuatrillones, quintillones.
2. Lea el número, comenzando con la escuela secundaria. En este caso, se llama el número de unidades de bits y el nombre de la clase.
3. Si el dígito es cero (el dígito está vacío), entonces no se llama. Si los tres dígitos de la clase llamada son ceros (los dígitos están vacíos), entonces no se llama a esta clase.

Leamos (nombre) el número escrito en la tabla (ver § 1), según los pasos 1 - 4. Divida mentalmente el número 38001102987000128425 en clases de derecha a izquierda: 038 001 102 987 000 128 425. Indiquemos los nombres de los Las clases en este número, comenzando desde el final, sus entradas son: unidades, miles, millones, billones, trillones, cuatrillones, quintillones. Ahora puede leer el número, comenzando con la clase senior. Nombramos números de tres dígitos, dos dígitos y un dígito, agregando el nombre de la clase correspondiente. Las clases vacías no se nombran. Obtenemos el siguiente número:

• 038 - treinta y ocho quintillones
• 001 - un cuatrillón
• 102 - ciento dos billones
• 987 - novecientos ochenta y siete mil millones
• 000 - no nombrar (no leer)
• 128 - ciento veintiocho mil
• 425 - cuatrocientos veinticinco

En consecuencia, el número natural 38 001 102 987 000 128 425 se lee de la siguiente manera: "treinta y ocho quintillones un cuatrillón ciento dos billones novecientos ochenta y siete mil ciento veintiocho mil cuatrocientos veinticinco".

1.9. El orden de escritura de los números naturales.

Los números naturales se escriben en el siguiente orden.

1. Escriba tres dígitos para cada clase, comenzando con la clase más alta hasta el dígito de las unidades. En este caso, para la clase superior de números, puede haber dos o uno.
2. Si no se nombra la clase o el rango, se escriben ceros en los dígitos correspondientes.

Por ejemplo, número veinticinco millones trescientos dos escrito en la forma: 25 000 302 (la clase de mil no se nombra, por lo tanto, se escriben ceros en todos los dígitos de la clase de mil).

1.10. Representación de números naturales como suma de términos de bits

Pongamos un ejemplo: 7 563 429 es la representación decimal del número siete millones quinientos sesenta y tres mil cuatrocientos veintinueve. Este número contiene siete millones quinientos mil, seis decenas de mil, tres mil cuatrocientos, dos decenas y nueve unidades. Se puede representar como una suma: 7,563,429 \u003d 7,000,000 + 500,000 + 60,000 + + 3,000 + 400 + 20 + 9. Tal entrada se denomina representación de un número natural como una suma de términos de bits.

Bloque 1.11. Vamos a jugar

Tesoros de mazmorras

En el campo de juego hay un dibujo del cuento de hadas de Kipling "Mowgli". Cinco cofres tienen candados. Para abrirlos, necesitas resolver problemas. Al mismo tiempo, cuando abres un cofre de madera, obtienes un punto. Cuando abres un cofre de hojalata, obtienes dos puntos, uno de cobre: ​​tres puntos, uno de plata: cuatro y uno de oro: cinco. El ganador es el que abre todos los cofres más rápido. El mismo juego se puede jugar en una computadora.

1. cofre de madera

Encuentra cuánto dinero (en miles de rublos) hay en este cofre. Para hacer esto, necesita encontrar el número total de unidades de bits menos significativas de la clase de millones para el número: 125308453231.

1. cofre de hojalata

Encuentra cuánto dinero (en miles de rublos) hay en este cofre. Para ello, en el número 12530845323 busque el número de unidades de bits menos significativas de la clase unidad y el número de unidades de bits menos significativas de la clase millón. Luego encuentre la suma de estos números y, a la derecha, atribuya el número en el lugar de las decenas de millones.

1. cofre de cobre

Para encontrar el dinero de este cofre (en miles de rublos), en el número 751305432198203 encuentre el número de unidades de dígitos más bajos en la clase de billones y el número de unidades de dígitos más bajos en la clase de mil millones. Luego encuentre la suma de estos números y a la derecha asigne los números naturales de la clase de unidades de este número en el orden de su disposición.

1. cofre de plata

El dinero de este cofre (en millones de rublos) se mostrará mediante la suma de dos números: el número de unidades de dígitos más bajos de la clase de miles y las unidades de dígitos promedio de la clase de mil millones para el número 481534185491502.

1. cofre dorado

Dado el número 800123456789123456789. Si multiplicamos los números en los dígitos más altos de todas las clases de este número, obtendremos el dinero de este cofre en millones de rublos.

Bloque 1.12. Fósforo

Escribe números naturales. Representación de números naturales como suma de términos de bits

Para cada tarea de la columna de la izquierda, elija una solución de la columna de la derecha. Escriba la respuesta en la forma: 1a; 2 g; 3b…

	Anota los números: cinco millones veinticinco mil
	Anota los números: cinco mil veinticinco millones
	Anota los números: cinco billones veinticinco
	Anota los números: setenta y siete millones setenta y siete mil setecientos setenta y siete
	Anota los números: setenta y siete billones setecientos setenta y siete mil siete
	Anota los números: setenta y siete millones setecientos setenta y siete mil siete
	Anota los números: ciento veintitrés mil cuatrocientos cincuenta y seis millones setecientos ochenta y nueve mil
	Anota los números: ciento veintitrés millones cuatrocientos cincuenta y seis mil setecientos ochenta y nueve
	Anota los números: tres mil once
	Anota los números: tres mil once millones

opcion 2

	treinta y dos mil ciento setenta y cinco millones doscientos noventa y ocho mil trescientos cuarenta y uno		100000000 + 1000000 + 10000 + 100 + 1
	Exprese el número como una suma de términos de bits: trescientos veintiun millones cuarenta y uno		30000000000 + 2000000000 + 100000000 + 70000000 + 5000000 + 200000 + 90000 + 8000 + 300 + 40 + 1
	Exprese el número como una suma de términos de bits: 321000175298341
	Exprese el número como una suma de términos de bits: 101010101
	Exprese el número como una suma de términos de bits: 11111		300000000 + 20000000 + 1000000 +
	5000000 + 300000 + 20000 + 1000
	Escriba en notación decimal el número representado como la suma de los bits: 5000000 + 300 + 20 + 1		30000000000000 + 2000000000000 + 1000000000000 + 100000000 + 70000000 + 5000000 + 200000 + 90000 + 8000 + 300 + 40 + 1
	Escriba en notación decimal el número representado como la suma de los bits: 10000000000 + 2000000000 + 100000 + 10 + 9
	Escriba en notación decimal el número representado como la suma de los bits: 10000000000 + 2000000000 + 100000000 + 10000000 + 9000000
	Escriba en notación decimal el número representado como la suma de los bits: 9000000000000 + 9000000000 + 9000000 + 9000 + 9		10000 + 1000 + 100 + 10 + 1

Bloque 1.13. Prueba de facetas

El nombre de la prueba proviene de la palabra "ojo compuesto de insectos". Este es un ojo compuesto, que consta de "ojos" separados. Las tareas de la prueba facetada se forman a partir de elementos separados, indicados por números. Por lo general, las pruebas facetadas contienen una gran cantidad de elementos. Pero solo hay cuatro tareas en esta prueba, pero están compuestas por una gran cantidad de elementos. Esto se hace para enseñarle cómo "recolectar" problemas de prueba. Si puede componerlos, entonces puede hacer frente fácilmente a otras pruebas de facetas.

Expliquemos cómo se componen las tareas usando el ejemplo de la tercera tarea. Se compone de elementos de prueba numerados: 1, 4, 7, 11, 1, 5, 7, 9, 10, 16, 17, 22, 21, 25

« Si» 1) tomar números de la tabla (número); 4) 7; 7) colocarlo en una categoría; 11) mil millones; 1) tomar un número de la tabla; 5) 8; 7) colóquelo en filas; 9) Decenas de millones; 10) cientos de millones; 16) cientos de miles; 17) Decenas de miles; 22) coloque los números 9 y 6 en los lugares de los millares y las centenas. 21) complete los dígitos restantes con ceros; " ESO» 26) obtenemos un número igual al tiempo (período) de la revolución del planeta Plutón alrededor del Sol en segundos (s); " este numero es»: 7880889600 s. En las respuestas, se indica con la letra "V".

Al resolver problemas, escriba los números en las celdas de la tabla con un lápiz.

Prueba de facetas. inventar un numero

La tabla contiene los números:

Si

1) tomar el número (números) de la tabla:

2) 4; 3) 5; 4) 7; 5) 8; 6) 9;

7) coloque esta cifra (números) en la categoría (dígitos);

8) cientos de cuatrillones y decenas de cuatrillones;

9) decenas de millones;

10) cientos de millones;

11) mil millones;

12) quintillones;

13) decenas de quintillones;

14) cientos de quintillones;

15) billones;

16) cientos de miles;

17) decenas de miles;

18) llenar la clase (clases) con ella (ellos);

19) quintillones;

20 billones;

21) complete los dígitos restantes con ceros;

22) coloque los números 9 y 6 en los lugares de los millares y centenas;

23) obtenemos un número igual a la masa de la Tierra en decenas de toneladas;

24) obtenemos un número aproximadamente igual al volumen de la Tierra en metros cúbicos;

25) obtenemos un número igual a la distancia (en metros) del Sol al planeta más lejano del sistema solar Plutón;

26) obtenemos un número igual al tiempo (período) de la revolución del planeta Plutón alrededor del Sol en segundos (s);

Este número es:

a) 5929000000000

b) 999990000000000000000

d) 5980000000000000000000

Resolver problemas:

1, 3, 6, 5, 18, 19, 21, 23

1, 6, 7, 14, 13, 12, 8, 21, 24

1, 4, 7, 11, 1, 5, 7, 10, 9, 16, 17, 22, 21, 26

1, 3, 7, 15, 1, 6, 2, 6, 18, 20, 21, 25

respuestas

1, 3, 6, 5, 18, 19, 21, 23-g

1, 6, 7, 14, 13, 12, 8, 21, 24 - b

1, 4, 7, 11, 1, 5, 7, 10, 9, 16, 17, 22, 21, 26 - en

1, 3, 7, 15, 1, 6, 2, 6, 18, 20, 21, 25 - un

En matemáticas, hay varios conjuntos diferentes de números: reales, complejos, enteros, racionales, irracionales, ... En nuestro La vida cotidiana la mayoría de las veces usamos números naturales, ya que los encontramos al contar y al buscar, indicando la cantidad de objetos.

En contacto con

¿Qué números se llaman naturales?

A partir de diez dígitos, puede anotar absolutamente cualquier suma existente de clases y rangos. Los valores naturales son aquellos que se utilizan:

• Al contar cualquier elemento (primero, segundo, tercero,... quinto,... décimo).
• Al indicar el número de artículos (uno, dos, tres...)

Los valores de N son siempre enteros y positivos. No existe N mayor, ya que el conjunto de valores enteros no está limitado.

¡Atención! Los números naturales se obtienen contando objetos o designando su cantidad.

Absolutamente cualquier número puede descomponerse y representarse como términos de bits, por ejemplo: 8.346.809=8 millones+346 mil+809 unidades.

Conjunto N

El conjunto N está en el conjunto real, entero y positivo. En el diagrama de conjuntos, estarían uno en el otro, ya que el conjunto de los naturales es parte de ellos.

El conjunto de los números naturales se denota con la letra N. Este conjunto tiene un principio pero no un final.

También hay un conjunto extendido N, donde se incluye el cero.

número natural más pequeño

En la mayoría de las escuelas de matemáticas, el valor más pequeño de N contado como una unidad, ya que la ausencia de objetos se considera vacía.

Pero en las escuelas matemáticas extranjeras, por ejemplo, en francés, se considera natural. La presencia del cero en la serie facilita la demostración algunos teoremas.

Un conjunto de valores N que incluye cero se llama extendido y se denota con el símbolo N0 (índice cero).

Serie de números naturales

Una fila N es una secuencia de todos los N conjuntos de dígitos. Esta secuencia no tiene fin.

La peculiaridad de la serie natural es que el siguiente número diferirá en uno del anterior, es decir, aumentará. Pero los significados no puede ser negativo.

¡Atención! Para la comodidad de contar, hay clases y categorías:

• Unidades (1, 2, 3),
• Decenas (10, 20, 30),
• Centenas (100, 200, 300),
• Miles (1000, 2000, 3000),
• Decenas de miles (30.000),
• Cientos de miles (800.000),
• Millones (4000000) etc.

Todo N

Todos los N están en el conjunto de valores reales, enteros, no negativos. Ellos son suyos parte integral.

Estos valores van al infinito, pueden pertenecer a las clases de millones, billones, quintillones, etc.

Por ejemplo:

• Cinco manzanas, tres gatitos,
• Diez rublos, treinta lápices,
• Cien kilogramos, trescientos libros,
• Un millón de estrellas, tres millones de personas, etc.

Secuencia en N

En diferentes escuelas matemáticas, se pueden encontrar dos intervalos a los que pertenece la sucesión N:

de cero a más infinito, incluidos los extremos, y de uno a más infinito, incluidos los extremos, es decir, todos respuestas enteras positivas.

N conjuntos de dígitos pueden ser pares o impares. Considere el concepto de rareza.

Impar (los impares terminan en los números 1, 3, 5, 7, 9.) con dos tienen un resto. Por ejemplo, 7:2=3,5, 11:2=5,5, 23:2=11,5.

¿Qué significa incluso N?

Todas las sumas pares de clases terminan en números: 0, 2, 4, 6, 8. Al dividir N pares entre 2, no quedará resto, es decir, el resultado es una respuesta entera. Por ejemplo, 50:2=25, 100:2=50, 3456:2=1728.

¡Importante! Una serie numérica de N no puede constar únicamente de valores pares o impares, ya que deben alternarse: un número par siempre va seguido de un número impar, luego de nuevo un número par, y así sucesivamente.

N propiedades

Como todos los demás conjuntos, N tiene sus propias propiedades especiales. Considere las propiedades de la serie N (no extendida).

• El valor que es el más pequeño y que no sigue a ningún otro es uno.
• N son una secuencia, es decir, un valor natural sigue a otro(a excepción de uno - es el primero).
• Cuando realizamos operaciones computacionales en N sumas de dígitos y clases (sumar, multiplicar), entonces la respuesta siempre sale natural significado.
• En los cálculos, puede utilizar la permutación y la combinación.
• Cada valor posterior no puede ser menor que el anterior. También en la serie N, operará la siguiente ley: si el número A es menor que B, entonces en la serie numérica siempre habrá una C, para la cual la igualdad es verdadera: A + C \u003d B.
• Si tomamos dos expresiones naturales, por ejemplo, A y B, entonces una de las expresiones será verdadera para ellas: A \u003d B, A es mayor que B, A es menor que B.
• Si A es menor que B y B es menor que C, entonces se sigue que que A es menor que C.
• Si A es menor que B, entonces se sigue que: si les sumamos la misma expresión (C), entonces A + C es menor que B + C. También es cierto que si estos valores se multiplican por C, entonces AC es menor que AB.
• Si B es mayor que A pero menor que C, entonces B-A es menor que C-A.

¡Atención! Todas las desigualdades anteriores también son válidas en la dirección opuesta.

¿Cómo se llaman las componentes de una multiplicación?

En muchas tareas simples e incluso complejas, encontrar la respuesta depende de la habilidad de los escolares.

Para poder multiplicar rápida y correctamente y poder resolver problemas inversos, necesitas conocer los componentes de la multiplicación.

15. 10=150. En esta expresión, 15 y 10 son factores, y 150 es un producto.

La multiplicación tiene propiedades que son necesarias a la hora de resolver problemas, ecuaciones y desigualdades:

• Reorganizar los factores no cambia el producto final.
• Para encontrar el factor desconocido, debe dividir el producto por el factor conocido (válido para todos los factores).

Por ejemplo: 15 . X=150. Divide el producto por un factor conocido. 150:15=10. Hagamos una comprobación. 15 . 10=150. De acuerdo con este principio, incluso ecuaciones lineales complejas(si los simplificas).

¡Importante! El producto puede constar de más de dos factores. Por ejemplo: 840=2 . 5. 7. 3. 4

¿Qué son los números naturales en matemáticas?

Descargas y clases de números naturales

Conclusión

Resumamos. N se utiliza al contar o indicar el número de elementos. El número de conjuntos naturales de dígitos es infinito, pero solo incluye sumas enteras y positivas de dígitos y clases. La multiplicación también es necesaria para contar cosas, así como para la resolución de problemas, ecuaciones y desigualdades diversas.

Las matemáticas surgieron de la filosofía general alrededor del siglo VI a. e., y desde ese momento inició su marcha victoriosa alrededor del mundo. Cada etapa de desarrollo introdujo algo nuevo: el conteo elemental evolucionó, se transformó en cálculo diferencial e integral, los siglos cambiaron, las fórmulas se volvieron cada vez más confusas y llegó el momento en que "comenzaron las matemáticas más complejas: todos los números desaparecieron". Pero ¿cuál fue la base?

el comienzo del tiempo

Los números naturales aparecieron junto con las primeras operaciones matemáticas. Una vez una columna vertebral, dos columnas vertebrales, tres columnas vertebrales ... Aparecieron gracias a los científicos indios que dedujeron la primera posición

La palabra "posicionalidad" significa que la ubicación de cada dígito en un número está estrictamente definida y corresponde a su categoría. Por ejemplo, los números 784 y 487 son los mismos números, pero los números no son equivalentes, ya que el primero incluye 7 centenas, mientras que el segundo solo 4. Los árabes recogieron la innovación de los indios, quienes llevaron los números a la forma que sabemos ahora.

En la antigüedad, a los números se les dio un significado místico, Pitágoras creía que el número subyace en la creación del mundo junto con los elementos principales: fuego, agua, tierra, aire. Si consideramos todo solo desde el punto de vista matemático, ¿qué es un número natural? El campo de los números naturales se denota como N y es una serie infinita de números que son enteros y positivos: 1, 2, 3,… + ∞. Se excluye el cero. Se utiliza principalmente para contar artículos e indicar el orden.

¿Qué hay en las matemáticas? axiomas de peano

El campo N es el campo base en el que se basan las matemáticas elementales. Con el tiempo, los campos de números enteros, racionales,

El trabajo del matemático italiano Giuseppe Peano hizo posible una mayor estructuración de la aritmética, logró su formalidad y allanó el camino para nuevas conclusiones que iban más allá del campo N.

Lo que es un número natural se aclaró anteriormente en un lenguaje sencillo, a continuación consideraremos una definición matemática basada en los axiomas de Peano.

• Uno se considera un número natural.
• El número que sigue a un número natural es un número natural.
• No hay número natural antes de uno.
• Si el número b sigue tanto al número c como al número d, entonces c=d.
• El axioma de inducción, que a su vez muestra lo que es un número natural: si alguna afirmación que depende de un parámetro es cierta para el número 1, entonces suponemos que también sirve para el número n del campo de los números naturales N. Entonces la afirmación es verdadera para n = 1 del campo de los números naturales N.

Operaciones básicas para el campo de los números naturales

Dado que el campo N se convirtió en el primero para cálculos matemáticos, tanto los dominios de definición como los rangos de valores de una serie de operaciones a continuación se refieren a él. Están cerrados y no. La principal diferencia es que se garantiza que las operaciones cerradas dejan un resultado dentro del conjunto N, sin importar los números involucrados. Basta con que sean naturales. El resultado de las interacciones numéricas restantes ya no es tan inequívoco y depende directamente de qué tipo de números están involucrados en la expresión, ya que puede contradecir la definición principal. Entonces, operaciones cerradas:

• suma - x + y = z, donde x, y, z están incluidos en el campo N;
• multiplicación - x * y = z, donde x, y, z están incluidos en el campo N;
• exponenciación - x y , donde x, y están incluidos en el campo N.

Las operaciones restantes, cuyo resultado puede no existir en el contexto de la definición "qué es un número natural", son las siguientes:

Propiedades de los números pertenecientes al campo N

Todo razonamiento matemático posterior se basará en las siguientes propiedades, las más triviales, pero no menos importantes.

• La propiedad conmutativa de la suma es x + y = y + x, donde los números x, y están incluidos en el cuerpo N. O el conocido "la suma no cambia por un cambio en los lugares de los términos".
• La propiedad conmutativa de la multiplicación es x * y = y * x, donde los números x, y están incluidos en el campo N.
• La propiedad asociativa de la suma es (x + y) + z = x + (y + z), donde x, y, z están incluidos en el campo N.
• La propiedad asociativa de la multiplicación es (x * y) * z = x * (y * z), donde los números x, y, z están incluidos en el campo N.
• propiedad de distribución - x (y + z) = x * y + x * z, donde los números x, y, z están incluidos en el campo N.

mesa pitagórica

Uno de los primeros pasos en el conocimiento de toda la estructura de las matemáticas elementales por parte de los escolares, después de haber comprendido por sí mismos qué números se llaman naturales, es la tabla de Pitágoras. Puede considerarse no solo desde el punto de vista de la ciencia, sino también como un valioso monumento científico.

Esta tabla de multiplicar ha sufrido una serie de cambios a lo largo del tiempo: se ha eliminado el cero y los números del 1 al 10 se denotan solos, sin tener en cuenta el orden (cientos, miles ...). Es una tabla en la que los encabezados de filas y columnas son números, y el contenido de las celdas de su intersección es igual a su producto.

En la práctica de la enseñanza en las últimas décadas ha surgido la necesidad de memorizar la tabla de Pitágoras “en orden”, es decir, la memorización iba primero. Se excluyó la multiplicación por 1 porque el resultado fue 1 o mayor. Mientras tanto, en la tabla a simple vista se puede ver un patrón: el producto de los números crece en un paso, que es igual al título de la línea. Así, el segundo factor nos muestra cuántas veces necesitamos tomar el primero para obtener el producto deseado. Este sistema es mucho más cómodo que el que se practicaba en la Edad Media: aun sabiendo qué es un número natural y lo trivial que es, la gente conseguía complicar su conteo cotidiano utilizando un sistema basado en potencias de dos.

Subconjunto como cuna de las matemáticas

Por el momento, el campo de los números naturales N se considera solo como uno de los subconjuntos de los números complejos, pero esto no los hace menos valiosos en la ciencia. Un número natural es lo primero que aprende un niño al estudiarse a sí mismo y al mundo que lo rodea. Un dedo, dos dedos ... Gracias a él, una persona desarrolla el pensamiento lógico, así como la capacidad de determinar la causa y deducir el efecto, allanando el camino para grandes descubrimientos.

Los números naturales son uno de los conceptos matemáticos más antiguos.

En el pasado lejano, las personas no sabían números, y cuando necesitaban contar objetos (animales, peces, etc.), lo hacían de manera diferente a como lo hacemos ahora.

Se comparó la cantidad de objetos con partes del cuerpo, por ejemplo, con los dedos de la mano, y dijeron: "Tengo tantas nueces como dedos en la mano".

Con el tiempo, la gente se dio cuenta de que cinco nueces, cinco cabras y cinco liebres tienen una propiedad común: su número es cinco.

¡Recordar!

enteros son números, a partir del 1, que se obtienen al contar objetos.

1, 2, 3, 4, 5…

número natural más pequeño — 1 .

número natural más grande no existe.

Al contar, el número cero no se usa. Por lo tanto, el cero no se considera un número natural.

La gente aprendió a escribir números mucho más tarde que a contar. En primer lugar, comenzaron a representar la unidad con un palo, luego con dos palos, el número 2, con tres, el número 3.

| — 1, || — 2, ||| — 3, ||||| — 5 …

Luego aparecieron signos especiales para designar números, los precursores de los números modernos. Los números que usamos para escribir números se originaron en la India hace unos 1500 años. Los árabes los trajeron a Europa, por eso se llaman números arábigos.

Hay diez dígitos en total: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Estos dígitos se pueden usar para escribir cualquier número natural.

¡Recordar!

serie natural es la secuencia de todos los números naturales:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …

En la serie natural, cada número es mayor que el anterior en 1.

La serie natural es infinita, no hay ningún número natural mayor en ella.

El sistema de conteo que usamos se llama posicional decimal.

Decimal porque 10 unidades de cada dígito forman 1 unidad del dígito más significativo. Posicional porque el valor de un dígito depende de su lugar en la notación de un número, es decir, del dígito en el que está escrito.

¡Importante!

Las clases que siguen al billón se nombran según los nombres latinos de los números. Cada unidad siguiente contiene mil anteriores.

• 1,000 billones = 1,000,000,000,000 = 1 billón ("tres" es latín para "tres")
• 1,000 billones = 1,000,000,000,000,000 = 1 cuatrillón ("quadra" en latín significa "cuatro")
• 1,000 cuatrillones = 1,000,000,000,000,000,000 = 1 quintillón ("quinta" en latín significa "cinco")

Sin embargo, los físicos han encontrado un número que supera el número de todos los átomos (las partículas más pequeñas de materia) en todo el universo.

Este número tiene un nombre especial - gogol. Un googol es un número que tiene 100 ceros.