Ejemplos de integral definida por partes. Resolver integrales en línea
Anteriormente, dada una función determinada, guiándonos por varias fórmulas y reglas, encontramos su derivada. La derivada tiene numerosos usos: es la velocidad del movimiento (o, más generalmente, la velocidad de cualquier proceso); el coeficiente angular de la tangente a la gráfica de la función; utilizando la derivada, puedes examinar la monotonicidad y los extremos de una función; Ayuda a resolver problemas de optimización.
Pero junto con el problema de encontrar la velocidad según una ley de movimiento conocida, también existe un problema inverso: el problema de restaurar la ley del movimiento según una velocidad conocida. Consideremos uno de estos problemas.
Ejemplo 1. Un punto material se mueve en línea recta, su velocidad en el tiempo t viene dada por la fórmula v=gt. Encuentra la ley del movimiento.
Solución. Sea s = s(t) la ley de movimiento deseada. Se sabe que s"(t) = v(t). Esto significa que para resolver el problema es necesario seleccionar una función s = s(t), cuya derivada sea igual a gt. No es difícil adivinar que \(s(t) = \frac(gt^ 2)(2) \).De hecho
\(s"(t) = \left(\frac(gt^2)(2) \right)" = \frac(g)(2)(t^2)" = \frac(g)(2) \ cdot 2t = gt\)
Respuesta: \(s(t) = \frac(gt^2)(2) \)
Observemos inmediatamente que el ejemplo se resuelve correctamente, pero de forma incompleta. Obtuvimos \(s(t) = \frac(gt^2)(2) \). De hecho, el problema tiene infinitas soluciones: cualquier función de la forma \(s(t) = \frac(gt^2)(2) + C\), donde C es una constante arbitraria, puede servir como ley de movimiento, ya que \(\left (\frac(gt^2)(2) +C \right)" = gt \)
Para hacer el problema más específico, tuvimos que arreglar la situación inicial: indicar la coordenada de un punto en movimiento en algún momento, por ejemplo en t = 0. Si, digamos, s(0) = s 0, entonces a partir del igualdad s(t) = (gt 2)/2 + C obtenemos: s(0) = 0 + C, es decir C = s 0. Ahora la ley del movimiento está definida de forma única: s(t) = (gt 2)/2 + s 0.
En matemáticas, las operaciones mutuamente inversas reciben diferentes nombres, se inventan notaciones especiales, por ejemplo: elevación al cuadrado (x 2) y raíz cuadrada (\(\sqrt(x) \)), seno (sin x) y arcoseno (arcsin x) y etc. El proceso de encontrar la derivada de una función dada se llama diferenciación, y la operación inversa, es decir, el proceso de encontrar una función a partir de una derivada dada, es integración.
El propio término “derivada” puede justificarse “en términos cotidianos”: la función y = f(x) “da origen” a una nueva función y" = f"(x). La función y = f(x) actúa como “padre”, pero los matemáticos, naturalmente, no la llaman “padre” o “productor”; dicen que lo es, en relación a la función y" = f"( x), imagen primaria o primitiva.
Definición. La función y = F(x) se llama antiderivada para la función y = f(x) en el intervalo X si la igualdad F"(x) = f(x) se cumple para \(x \in X\)
En la práctica, el intervalo X no suele especificarse, pero está implícito (como dominio natural de definición de la función).
Pongamos ejemplos.
1) La función y = x 2 es antiderivada para la función y = 2x, ya que para cualquier x la igualdad (x 2)" = 2x es verdadera
2) La función y = x 3 es antiderivada para la función y = 3x 2, ya que para cualquier x la igualdad (x 3)" = 3x 2 es cierta
3) La función y = sin(x) es antiderivada para la función y = cos(x), ya que para cualquier x la igualdad (sin(x))" = cos(x) es verdadera
Al encontrar antiderivadas, así como derivadas, no solo se utilizan fórmulas, sino también algunas reglas. Están directamente relacionados con las reglas correspondientes para el cálculo de derivados.
Sabemos que la derivada de una suma es igual a la suma de sus derivadas. Esta regla genera la regla correspondiente para encontrar antiderivadas.
Regla 1. La antiderivada de una suma es igual a la suma de las antiderivadas.
Sabemos que el factor constante se puede quitar del signo de la derivada. Esta regla genera la regla correspondiente para encontrar antiderivadas.
Regla 2. Si F(x) es una antiderivada de f(x), entonces kF(x) es una antiderivada de kf(x).
Teorema 1. Si y = F(x) es una primitiva de la función y = f(x), entonces la primitiva de la función y = f(kx + m) es la función \(y=\frac(1)(k)F (kx+m) \)
Teorema 2. Si y = F(x) es una primitiva de la función y = f(x) en el intervalo X, entonces la función y = f(x) tiene infinitas primitivas, y todas tienen la forma y = F(x) + C.
Métodos de integración
Método de reemplazo de variables (método de sustitución)
El método de integración por sustitución implica introducir una nueva variable de integración (es decir, sustitución). En este caso, la integral dada se reduce a una nueva integral, que es tabular o reducible a ella. No existen métodos generales para seleccionar sustituciones. La capacidad de determinar correctamente la sustitución se adquiere mediante la práctica.
Sea necesario calcular la integral \(\textstyle \int F(x)dx \). Hagamos la sustitución \(x= \varphi(t) \) donde \(\varphi(t) \) es una función que tiene una derivada continua.
Entonces \(dx = \varphi " (t) \cdot dt \) y con base en la propiedad de invariancia de la fórmula de integración para la integral indefinida, obtenemos la fórmula de integración por sustitución:
\(\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt \)
Integración de expresiones de la forma \(\textstyle \int \sin^n x \cos^m x dx \)
Si m es impar, m > 0, entonces es más conveniente hacer la sustitución sen x = t.
Si n es impar, n > 0, entonces es más conveniente hacer la sustitución cos x = t.
Si n y m son pares, entonces es más conveniente realizar la sustitución tg x = t.
Integración por partes
Integración por partes - aplicando la siguiente fórmula de integración:
\(\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du \)
o:
\(\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx \)
Tabla de integrales indefinidas (antiderivadas) de algunas funciones
$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) +C\;\; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(arcsin) x +C $$ $$ \int \frac(dx)(1+x^2 ) = \text(arctg) x +C $$ $$ \int \text(ch) x dx = \text(sh) x +C $$ $$ \int \text(sh) x dx = \text(ch )x+C$$Integración por partes. Ejemplos de soluciones
Hola de nuevo. Hoy en la lección aprenderemos a integrar por partes. El método de integración por partes es uno de los pilares del cálculo integral. Durante las pruebas o exámenes, casi siempre se pide a los estudiantes que resuelvan los siguientes tipos de integrales: la integral más simple (ver artículo) o una integral reemplazando una variable (ver artículo) o la integral está justo en método de integración por partes.
Como siempre, deberás tener a mano: Tabla de integrales Y tabla de derivados. Si aún no los tienes, visita el trastero de mi web: Fórmulas y tablas matemáticas.. No me cansaré de repetirlo: es mejor imprimirlo todo. Intentaré presentar todo el material de forma coherente, sencilla y clara, no hay dificultades especiales para integrar las partes.
¿Qué problema resuelve el método de integración por partes? El método de integración por partes resuelve un problema muy importante, permite integrar algunas funciones que no están en la tabla, trabajar funciones y, en algunos casos, incluso cocientes. Como recordamos, no existe una fórmula conveniente: ![]() . Pero existe este:
. Pero existe este: ![]() – Fórmula de integración por partes presencial. Lo sé, lo sé, eres la única; trabajaremos con ella durante toda la lección (ahora es más fácil).
– Fórmula de integración por partes presencial. Lo sé, lo sé, eres la única; trabajaremos con ella durante toda la lección (ahora es más fácil).
E inmediatamente la lista al estudio. Las integrales de los siguientes tipos se toman por partes:
1) , ![]() , – logaritmo, logaritmo multiplicado por algún polinomio.
, – logaritmo, logaritmo multiplicado por algún polinomio.
2) ,![]() es una función exponencial multiplicada por algún polinomio. Esto también incluye integrales como: una función exponencial multiplicada por un polinomio, pero en la práctica es 97 por ciento, debajo de la integral hay una bonita letra "e". ... el artículo resulta algo lírico, oh sí ... ha llegado la primavera.
es una función exponencial multiplicada por algún polinomio. Esto también incluye integrales como: una función exponencial multiplicada por un polinomio, pero en la práctica es 97 por ciento, debajo de la integral hay una bonita letra "e". ... el artículo resulta algo lírico, oh sí ... ha llegado la primavera.
3) , ![]() , son funciones trigonométricas multiplicadas por algún polinomio.
, son funciones trigonométricas multiplicadas por algún polinomio.
4), – funciones trigonométricas inversas (“arcos”), “arcos” multiplicados por algún polinomio.
Algunas fracciones también se toman en partes, también consideraremos los ejemplos correspondientes en detalle.
Integrales de logaritmos
Ejemplo 1
Clásico. De vez en cuando, esta integral se puede encontrar en tablas, pero no es aconsejable utilizar una respuesta ya preparada, ya que el profesor tiene deficiencia de vitaminas primaverales y maldecirá mucho. Porque la integral considerada no es en modo alguno tabular: se toma en partes. Nosotros decidimos:
Interrumpimos la solución para explicaciones intermedias.
Usamos la fórmula de integración por partes: ![]()
La fórmula se aplica de izquierda a derecha.
Nos fijamos en el lado izquierdo: . Obviamente, en nuestro ejemplo (y en todos los demás que consideraremos), algo debe designarse como y algo como .
En integrales del tipo considerado, siempre se denota el logaritmo.
Técnicamente, el diseño de la solución se implementa de la siguiente manera, escribimos en la columna:
Es decir, denotamos el logaritmo por y por - la parte restante expresión integrando.
Siguiente etapa: encontrar el diferencial:

Un diferencial es casi lo mismo que una derivada; ya hemos discutido cómo encontrarlo en lecciones anteriores.
Ahora encontramos la función. Para encontrar la función que necesita integrar lado derecho menor igualdad:

Ahora abrimos nuestra solución y construimos el lado derecho de la fórmula: .
Por cierto, aquí tenéis una muestra de la solución final con algunas notas:

El único punto del trabajo es que inmediatamente cambié y , ya que es costumbre escribir el factor antes del logaritmo.
Como puede ver, la aplicación de la fórmula de integración por partes esencialmente redujo nuestra solución a dos integrales simples.
Tenga en cuenta que en algunos casos justo después de Al aplicar la fórmula, necesariamente se realiza una simplificación en la integral restante; en el ejemplo considerado, reducimos el integrando a "x".
Vamos a revisar. Para hacer esto, debes tomar la derivada de la respuesta:
Se ha obtenido la función integrando original, lo que significa que la integral se ha resuelto correctamente.
Durante la prueba utilizamos la regla de diferenciación de productos: ![]() . Y esto no es una coincidencia.
. Y esto no es una coincidencia.
Fórmula de integración por partes. ![]() y fórmula
y fórmula ![]() – estas son dos reglas mutuamente inversas.
– estas son dos reglas mutuamente inversas.
Ejemplo 2
Encuentra la integral indefinida.
El integrando es el producto de un logaritmo y un polinomio.
Vamos a decidir.
![]()
Una vez más describiré en detalle el procedimiento para aplicar la regla, en el futuro los ejemplos se presentarán más brevemente y, si tiene dificultades para resolverlo usted mismo, debe volver a los dos primeros ejemplos de la lección. .
Como ya se mencionó, es necesario denotar el logaritmo (no importa el hecho de que sea una potencia). denotamos por la parte restante expresión integrando.
Escribimos en la columna:
Primero encontramos el diferencial:

Aquí usamos la regla para derivar una función compleja. ![]() . No es casualidad que en la primera lección del tema Integral indefinida. Ejemplos de soluciones Me centré en el hecho de que para dominar las integrales, es necesario "tener en sus manos" las derivadas. Tendrás que lidiar con derivados más de una vez.
. No es casualidad que en la primera lección del tema Integral indefinida. Ejemplos de soluciones Me centré en el hecho de que para dominar las integrales, es necesario "tener en sus manos" las derivadas. Tendrás que lidiar con derivados más de una vez.
Ahora encontramos la función, para ello integramos lado derecho menor igualdad:

Para la integración utilizamos la fórmula tabular más simple. ![]()
Ahora todo está listo para aplicar la fórmula. ![]() . Abra con un asterisco y “construya” la solución de acuerdo con el lado derecho:
. Abra con un asterisco y “construya” la solución de acuerdo con el lado derecho:
¡Bajo la integral tenemos nuevamente un polinomio para el logaritmo! Por tanto, se vuelve a interrumpir la solución y se aplica por segunda vez la regla de integración por partes. No olvide que en situaciones similares siempre se denota el logaritmo.

Sería bueno que ya supieras cómo encontrar las integrales y derivadas más simples de forma oral.

(1) ¡No te confundas con las señales! Muy a menudo el menos se pierde aquí, tenga en cuenta también que el menos se refiere a a todos soporte  , y estos corchetes deben expandirse correctamente.
, y estos corchetes deben expandirse correctamente.
(2) Abra los soportes. Simplificamos la última integral.
(3) Tomamos la última integral.
(4) “Combinar” la respuesta.
La necesidad de aplicar la regla de integración por partes dos veces (o incluso tres veces) no surge muy raramente.
Y ahora un par de ejemplos para su propia solución:
Ejemplo 3
Encuentra la integral indefinida.
¡Este ejemplo se resuelve cambiando la variable (o sustituyéndola bajo el signo diferencial)! ¿Por qué no? Puedes intentar hacerlo en partes, resultará algo divertido.
Ejemplo 4
Encuentra la integral indefinida.
Pero esta integral está integrada por partes (la fracción prometida).
Estos son ejemplos para que los resuelvas por tu cuenta, soluciones y respuestas al final de la lección.
Parece que en los ejemplos 3 y 4 los integrandos son similares, ¡pero los métodos de solución son diferentes! Ésta es la principal dificultad para dominar las integrales: si eliges el método incorrecto para resolver una integral, podrás jugar con ella durante horas, como con un rompecabezas real. Por lo tanto, cuanto más resuelvas varias integrales, mejor y más fácil será la prueba y el examen. Además, en el segundo año habrá ecuaciones diferenciales, y sin experiencia en la resolución de integrales y derivadas no hay nada que hacer allí.
En términos de logaritmos, esto probablemente sea más que suficiente. Además, también recuerdo que los estudiantes de ingeniería usan logaritmos para llamar a los senos femeninos =). Por cierto, es útil conocer de memoria las gráficas de las principales funciones elementales: seno, coseno, arcotangente, exponente, polinomios de tercer, cuarto grado, etc. No, por supuesto, un condón en el mundo.
No lo estiraré, pero ahora recordarás mucho de la sección. Gráficos y funciones =).
Integrales de una exponencial multiplicada por un polinomio
Regla general:
Ejemplo 5
Encuentra la integral indefinida.
![]()
Usando un algoritmo familiar, integramos por partes:


Si tienes dificultades con la integral, deberías volver al artículo. Método de cambio de variable en integral indefinida..
Lo único que puedes hacer es modificar la respuesta:

Pero si tu técnica de cálculo no es muy buena, entonces la opción más rentable es dejarla como respuesta. ![]() o incluso
o incluso ![]()
Es decir, el ejemplo se considera resuelto cuando se toma la última integral. No será un error, otra cosa es que el profesor te pida que simplifiques la respuesta.
Ejemplo 6
Encuentra la integral indefinida.
Este es un ejemplo para que lo resuelvas por tu cuenta. Esta integral se integra dos veces por partes. Se debe prestar especial atención a los signos: es fácil confundirse con ellos, también recordamos que se trata de una función compleja.
No hay nada más que decir sobre el expositor. Solo puedo agregar que el logaritmo exponencial y natural son funciones mutuamente inversas, este soy yo sobre el tema de las gráficas entretenidas de matemáticas superiores =) Detente, detente, no te preocupes, el profesor está sobrio.
Integrales de funciones trigonométricas multiplicadas por un polinomio
Regla general: porque siempre denota un polinomio
Ejemplo 7
Encuentra la integral indefinida.
![]()
Integramos por partes:


Mmmm...y no hay nada que comentar.
Ejemplo 8
Encuentra la integral indefinida ![]()
Este es un ejemplo para que lo resuelvas tú mismo.
Ejemplo 9
Encuentra la integral indefinida
Otro ejemplo con una fracción. Como en los dos ejemplos anteriores, for denota un polinomio.
Integramos por partes: 

Si tiene alguna dificultad o malentendido para encontrar la integral, le recomiendo asistir a la lección. Integrales de funciones trigonométricas..
Ejemplo 10
Encuentra la integral indefinida ![]()
Este es un ejemplo para que lo resuelvas por tu cuenta.
Sugerencia: antes de usar el método de integración por partes, debes aplicar alguna fórmula trigonométrica que convierta el producto de dos funciones trigonométricas en una sola función. La fórmula también se puede utilizar al aplicar el método de integración por partes, el que te resulte más conveniente.
Probablemente eso esté todo en este párrafo. Por alguna razón recordé una línea del himno de física y matemáticas “Y el gráfico sinusoidal corre onda tras onda a lo largo del eje de abscisas”….
Integrales de funciones trigonométricas inversas.
Integrales de funciones trigonométricas inversas multiplicadas por un polinomio
Regla general: siempre denota la función trigonométrica inversa.
Permítanme recordarles que las funciones trigonométricas inversas incluyen arcoseno, arcocoseno, arcotangente y arcocotangente. En aras de la brevedad del registro los llamaré "arcos".

 al cálculo de la integral
al cálculo de la integral  , que resulta ser más simple que este.
, que resulta ser más simple que este. ,
, ,
, , Dónde
, Dónde  – polinomio,
– polinomio,  – un número distinto de cero
– un número distinto de cero denotar un polinomio
denotar un polinomio 
 .
. ,
, ,
, ,
, ,
, , Dónde
, Dónde  – polinomio.
– polinomio. denotar
denotar  , y el resto del integrando a través
, y el resto del integrando a través  :
: ,
, , Dónde
, Dónde  – números.
– números. denotar
denotar  y aplicar la fórmula de integración por partes dos veces, volviendo como resultado a la integral original, luego de lo cual la integral original se expresa a partir de la igualdad.
y aplicar la fórmula de integración por partes dos veces, volviendo como resultado a la integral original, luego de lo cual la integral original se expresa a partir de la igualdad. ; b)
; b)  .
.
 , Dónde
, Dónde  – polinomio de grado
– polinomio de grado  ,
, – polinomio de grado
– polinomio de grado
 .
. , de lo contrario (si
, de lo contrario (si  ) la fracción racional se llama equivocado.
) la fracción racional se llama equivocado. y una fracción racional propia dividiendo el numerador por el denominador según la regla para dividir polinomios:
y una fracción racional propia dividiendo el numerador por el denominador según la regla para dividir polinomios: ,
, – parte entera de la división,
– parte entera de la división,  – fracción racional propia,
– fracción racional propia,  - resto de la división.
- resto de la división. ;
; ;
; ;
; ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 – números reales y
– números reales y  (es decir, el trinomio cuadrado en el denominador de las fracciones III y IV no tiene raíces; el discriminante es negativo) se llaman fracciones racionales simples I, II, III y IV tipos.
(es decir, el trinomio cuadrado en el denominador de las fracciones III y IV no tiene raíces; el discriminante es negativo) se llaman fracciones racionales simples I, II, III y IV tipos. .
. .
. . Después de la sustitución, la integral se divide en dos integrales. La primera integral se calcula aislando la derivada del denominador en el numerador, lo que da una integral tabular, y la segunda integral se convierte a la forma
. Después de la sustitución, la integral se divide en dos integrales. La primera integral se calcula aislando la derivada del denominador en el numerador, lo que da una integral tabular, y la segunda integral se convierte a la forma  , porque
, porque  , que también da la integral tabular.
, que también da la integral tabular.

 ;
; . Después de la sustitución, la integral se divide en dos integrales. La primera integral se calcula por sustitución.
. Después de la sustitución, la integral se divide en dos integrales. La primera integral se calcula por sustitución.  , y el segundo usando relaciones de recurrencia.
, y el segundo usando relaciones de recurrencia. ; b)
; b)  ; V)
; V)  .
. .
. corresponde a una fracción de la forma
corresponde a una fracción de la forma  ;
; corresponde a la cantidad
corresponde a la cantidad  fracciones de la forma
fracciones de la forma corresponde a una fracción de la forma
corresponde a una fracción de la forma  ;
; corresponde a la cantidad
corresponde a la cantidad  fracciones de la forma
fracciones de la forma . Igualar coeficientes en los mismos grados
. Igualar coeficientes en los mismos grados  en los polinomios de los lados izquierdo y derecho, obtenemos un sistema de ecuaciones lineales. Al resolver el sistema, determinamos los coeficientes inciertos.
en los polinomios de los lados izquierdo y derecho, obtenemos un sistema de ecuaciones lineales. Al resolver el sistema, determinamos los coeficientes inciertos. a los lados izquierdo y derecho de cualquier número, obtenemos una igualdad verdadera, lineal con respecto a los coeficientes desconocidos. Sustituyendo tantos valores
a los lados izquierdo y derecho de cualquier número, obtenemos una igualdad verdadera, lineal con respecto a los coeficientes desconocidos. Sustituyendo tantos valores  , cuántos coeficientes desconocidos hay, obtenemos un sistema de ecuaciones lineales. En lugar de
, cuántos coeficientes desconocidos hay, obtenemos un sistema de ecuaciones lineales. En lugar de  Puedes sustituir cualquier número en los lados izquierdo y derecho, pero es más conveniente sustituir las raíces de los denominadores de fracciones.
Puedes sustituir cualquier número en los lados izquierdo y derecho, pero es más conveniente sustituir las raíces de los denominadores de fracciones. ; b)
; b)  ; V)
; V)  .
. .
.
 .
. , obtenemos:
, obtenemos:



 .
. .
. .
. .
. , obtenemos el sistema:
, obtenemos el sistema:








 .
.
 .
. .
. .
. valores parciales, en los que los factores desaparecen, es decir, sustituimos estos valores en la última expresión y obtenemos tres ecuaciones:
valores parciales, en los que los factores desaparecen, es decir, sustituimos estos valores en la última expresión y obtenemos tres ecuaciones:
 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.


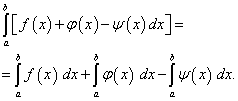 (42)
(42)




