Expansiunea seriei Taylor a cos. Extinderea funcțiilor în serii de puteri
16.1. Extinderea funcțiilor elementare în seria Taylor și
Maclaurin
Să arătăm că dacă pe o mulțime este definită o funcție arbitrară  , în vecinătatea punctului
, în vecinătatea punctului  are multe derivate și este suma unei serii de puteri:
are multe derivate și este suma unei serii de puteri:
atunci puteți găsi coeficienții acestei serii.
Să înlocuim într-o serie de puteri  . Apoi
. Apoi  .
.
Să găsim prima derivată a funcției  :
:
La  :
: .
.
Pentru derivata a doua obținem:
La  :
: .
.
Continuând această procedură n odată ce obținem:  .
.
Astfel, am obținut o serie de puteri de forma:


 ,
,
Care e numit lângă Taylor pentru functie  în vecinătatea punctului
în vecinătatea punctului  .
.
Un caz special al seriei Taylor este Seria Maclaurin la  :
:



Restul seriei Taylor (Maclaurin) se obține prin eliminarea seriei principale n primii membri și se notează ca  . Apoi funcția
. Apoi funcția  poate fi scris ca o sumă n primii membri ai seriei
poate fi scris ca o sumă n primii membri ai seriei  iar restul
iar restul  :,
:,
 .
.
Restul este de obicei  exprimate în formule diferite.
exprimate în formule diferite.
Una dintre ele este în formă Lagrange:
 , Unde
, Unde  .
. .
.
Rețineți că, în practică, seria Maclaurin este folosită mai des. Astfel, pentru a scrie funcția  sub forma unei sume de serie de puteri este necesar:
sub forma unei sume de serie de puteri este necesar:
1) găsiți coeficienții seriei Maclaurin (Taylor);
2) găsiți regiunea de convergență a seriei de puteri rezultate;
3) demonstrați că această serie converge către funcția  .
.
Teorema1
(o condiție necesară și suficientă pentru convergența seriei Maclaurin). Fie raza de convergență a seriei  . Pentru ca această serie să convergă în interval
. Pentru ca această serie să convergă în interval  a functiona
a functiona  , este necesar și suficient ca condiția să fie îndeplinită:
, este necesar și suficient ca condiția să fie îndeplinită:  în intervalul specificat.
în intervalul specificat.
Teorema 2. Dacă derivate de orice ordin al funcției  într-un anumit interval
într-un anumit interval  limitată în valoare absolută la același număr M, acesta este
limitată în valoare absolută la același număr M, acesta este  , apoi în acest interval funcția
, apoi în acest interval funcția  poate fi extins într-o serie Maclaurin.
poate fi extins într-o serie Maclaurin.
Exemplu1
.
Extindeți într-o serie Taylor în jurul punctului  funcţie.
funcţie.
Soluţie.
 .
.
 ,;
,;
 ,
, ;
;
 ,
, ;
;
 ,
,
.......................................................................................................................................
 ,
, ;
;
Regiunea de convergență  .
.
Exemplu2
.
Extindeți o funcție  într-o serie Taylor în jurul unui punct
într-o serie Taylor în jurul unui punct  .
.
Soluţie:
Aflați valoarea funcției și a derivatelor sale la  .
.
 ,
, ;
;
 ,
, ;
;
...........……………………………
 ,
, .
.
Să punem aceste valori la rând. Primim:
sau  .
.
Să găsim regiunea de convergență a acestei serii. Conform testului lui d'Alembert, o serie converge dacă
 .
.
Prin urmare, pentru orice  această limită este mai mică de 1 și, prin urmare, domeniul de convergență al seriei va fi:
această limită este mai mică de 1 și, prin urmare, domeniul de convergență al seriei va fi:  .
.
Să luăm în considerare câteva exemple de extindere a seriei Maclaurin a funcțiilor elementare de bază. Amintiți-vă că seria Maclaurin:


 .
.
converge asupra intervalului  a functiona
a functiona  .
.
Rețineți că pentru a extinde o funcție într-o serie este necesar:
a) găsiți coeficienții seriei Maclaurin pentru această funcție;
b) se calculează raza de convergenţă pentru seria rezultată;
c) demonstrați că seria rezultată converge către funcție  .
.
Exemplul 3. Luați în considerare funcția  .
.
Soluţie.
Să calculăm valoarea funcției și a derivatelor sale la  .
.
Atunci coeficienții numerici ai seriei au forma:
pentru oricine n. Să înlocuim coeficienții găsiți în seria Maclaurin și să obținem: 
Să găsim raza de convergență a seriei rezultate și anume:
 .
.
Prin urmare, seria converge asupra intervalului  .
.
Această serie converge către funcția  pentru orice valoare
pentru orice valoare  , deoarece pe orice interval
, deoarece pe orice interval  funcţie
funcţie  iar derivatele sale de valoare absolută sunt limitate ca număr
iar derivatele sale de valoare absolută sunt limitate ca număr  .
.
Exemplu4
.
Luați în considerare funcția  .
.
Soluţie.
 :
:

Este ușor de observat că derivatele de ordin egal  , iar derivatele sunt de ordin impar. Să substituim coeficienții găsiți în seria Maclaurin și să obținem expansiunea:
, iar derivatele sunt de ordin impar. Să substituim coeficienții găsiți în seria Maclaurin și să obținem expansiunea:
Să găsim intervalul de convergență al acestei serii. Conform semnului lui d'Alembert:
pentru oricine  . Prin urmare, seria converge asupra intervalului
. Prin urmare, seria converge asupra intervalului  .
.
Această serie converge către funcția  , deoarece toate derivatele sale sunt limitate la unitate.
, deoarece toate derivatele sale sunt limitate la unitate.
Exemplu5
.
 .
.
Soluţie.
Să găsim valoarea funcției și a derivatelor sale la  :
:

Astfel, coeficienții acestei serii:  Și
Și  , prin urmare:
, prin urmare:
Similar cu rândul anterior, zona de convergență  . Seria converge către funcție
. Seria converge către funcție  , deoarece toate derivatele sale sunt limitate la unitate.
, deoarece toate derivatele sale sunt limitate la unitate.
Vă rugăm să rețineți că funcția  extindere impară și în serie în puteri impare, funcție
extindere impară și în serie în puteri impare, funcție  – par și extindere într-o serie în puteri egale.
– par și extindere într-o serie în puteri egale.
Exemplu6
.
Seria binomială:  .
.
Soluţie.
Să găsim valoarea funcției și a derivatelor sale la  :
:

Din aceasta se poate observa că:

Să substituim aceste valori ale coeficientului în seria Maclaurin și să obținem extinderea acestei funcții într-o serie de puteri:
Să găsim raza de convergență a acestei serii:

Prin urmare, seria converge asupra intervalului  . La punctele limitatoare la
. La punctele limitatoare la  Și
Și  o serie poate sau nu converge în funcție de exponent
o serie poate sau nu converge în funcție de exponent  .
.
Seria studiată converge asupra intervalului  a functiona
a functiona  , adică suma seriei
, adică suma seriei  la
la  .
.
Exemplu7
.
Să extindem funcția din seria Maclaurin  .
.
Soluţie.
Pentru a extinde această funcție într-o serie, folosim seria binomială la  . Primim:
. Primim: 
Pe baza proprietății seriei de puteri (o serie de puteri poate fi integrată în regiunea convergenței sale), găsim integrala părților din stânga și din dreapta acestei serii:
Să găsim zona de convergență a acestei serii:  ,
,
adică aria de convergență a acestei serii este intervalul  . Să determinăm convergența seriei la capetele intervalului. La
. Să determinăm convergența seriei la capetele intervalului. La 
 . Această serie este o serie armonioasă, adică diverge. La
. Această serie este o serie armonioasă, adică diverge. La  obținem o serie de numere cu un termen comun
obținem o serie de numere cu un termen comun  .
.
Seria converge conform testului lui Leibniz. Astfel, regiunea de convergență a acestei serii este intervalul  .
.
16.2. Aplicarea seriilor de puteri în calcule aproximative
În calculele aproximative, seriile de putere joacă un rol extrem de important. Cu ajutorul lor, au fost întocmite tabele de funcții trigonometrice, tabele de logaritmi, tabele de valori ale altor funcții, care sunt utilizate în diferite domenii de cunoaștere, de exemplu, în teoria probabilităților și statistica matematică. În plus, extinderea funcțiilor într-o serie de puteri este utilă pentru studiul lor teoretic. Problema principală atunci când se utilizează seriile de putere în calcule aproximative este problema estimării erorii la înlocuirea sumei unei serii cu suma primei sale. n membrii.
Să luăm în considerare două cazuri:
funcția este extinsă într-o serie alternantă de semne;
funcția este extinsă într-o serie de semn constant.
Calcul folosind serii alternative
Lasă funcția  extins într-o serie de puteri alternante. Apoi, când se calculează această funcție pentru o anumită valoare
extins într-o serie de puteri alternante. Apoi, când se calculează această funcție pentru o anumită valoare  obţinem o serie de numere la care putem aplica criteriul Leibniz. În conformitate cu acest criteriu, dacă suma unei serii este înlocuită cu suma primei sale n termeni, atunci eroarea absolută nu depășește primul termen din restul acestei serii, adică:
obţinem o serie de numere la care putem aplica criteriul Leibniz. În conformitate cu acest criteriu, dacă suma unei serii este înlocuită cu suma primei sale n termeni, atunci eroarea absolută nu depășește primul termen din restul acestei serii, adică:  .
.
Exemplu8
.
calculati  cu o precizie de 0,0001.
cu o precizie de 0,0001.
Soluţie.
Vom folosi seria Maclaurin pentru  , înlocuind valoarea unghiului în radiani:
, înlocuind valoarea unghiului în radiani:

Dacă comparăm primul și al doilea termen al seriei cu o precizie dată, atunci: .
Al treilea termen de extindere:
mai mică decât precizia de calcul specificată. Prin urmare, pentru a calcula  este suficient să lași doi termeni ai seriei, adică
este suficient să lași doi termeni ai seriei, adică
 .
.
Prin urmare  .
.
Exemplu9
.
calculati  cu o precizie de 0,001.
cu o precizie de 0,001.
Soluţie.
Vom folosi formula seriei binomiale. Pentru a face asta, hai să scriem  la fel de:
la fel de:  .
.
În această expresie  ,
,

Să comparăm fiecare dintre termenii seriei cu precizia specificată. Este clar că  . Prin urmare, pentru a calcula
. Prin urmare, pentru a calcula  este suficient să lăsați trei termeni din serie.
este suficient să lăsați trei termeni din serie.
 sau
sau  .
.
Calcul folosind serii pozitive
Exemplu10
.
Calculați numărul  cu o precizie de 0,001.
cu o precizie de 0,001.
Soluţie.
Într-un rând pentru o funcție  hai sa inlocuim
hai sa inlocuim  . Primim:
. Primim:

Să estimăm eroarea care apare la înlocuirea sumei unei serii cu suma primei  membrii. Să notăm inegalitatea evidentă:
membrii. Să notăm inegalitatea evidentă:
adica 2< <3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
<3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
 ,
, .
.
În funcție de problemă, trebuie să găsiți n astfel încât să fie valabilă următoarea inegalitate:  sau
sau  .
.
Este ușor să verifici când n= 6: .
.
Prin urmare,  .
.
Exemplu11
.
calculati  cu o precizie de 0,0001.
cu o precizie de 0,0001.
Soluţie.
Rețineți că pentru a calcula logaritmi se poate folosi o serie pentru funcție  , dar această serie converge foarte lent și pentru a obține precizia dată ar fi necesar să luăm 9999 de termeni! Prin urmare, pentru a calcula logaritmii, de regulă, se utilizează o serie pentru funcție
, dar această serie converge foarte lent și pentru a obține precizia dată ar fi necesar să luăm 9999 de termeni! Prin urmare, pentru a calcula logaritmii, de regulă, se utilizează o serie pentru funcție  , care converge asupra intervalului
, care converge asupra intervalului  .
.
Să calculăm  folosind această serie. Lăsa
folosind această serie. Lăsa  , Apoi
, Apoi  .
.
Prin urmare,  ,
,
Pentru a calcula  cu o precizie dată, luați suma primilor patru termeni:
cu o precizie dată, luați suma primilor patru termeni:  .
.
Restul seriei  hai să-l aruncăm. Să estimăm eroarea. Este evident că
hai să-l aruncăm. Să estimăm eroarea. Este evident că 
sau  .
.

Astfel, în seria care a fost folosită pentru calcul, a fost suficient să luăm doar primii patru termeni în loc de 9999 din serie pentru funcția  .
.
Întrebări de autodiagnosticare
1. Ce este o serie Taylor?
2. ce formă a avut seria Maclaurin?
3. Formulați o teoremă privind expansiunea unei funcții dintr-o serie Taylor.
4. Notați extinderea seriei Maclaurin a funcțiilor principale.
5. Indicați zonele de convergență ale seriei luate în considerare.
6. Cum se estimează eroarea în calcule aproximative folosind seriile de putere?
Dacă funcția f(x) are derivate de toate ordinele pe un anumit interval care conține punctul a, atunci i se poate aplica formula Taylor:
,
Unde r n– așa-numitul termen de rest sau rest al seriei, poate fi estimat folosind formula Lagrange:
, unde numărul x este între x și a.
Reguli de intrare în funcții:
Dacă pentru o anumită valoare X r n→0 la n→∞, atunci în limită formula Taylor devine convergentă pentru această valoare Seria Taylor:
,
Astfel, funcția f(x) poate fi extinsă într-o serie Taylor în punctul x luat în considerare dacă:
1) are derivate de toate ordinele;
2) seria construită converge în acest punct.
Când a = 0 obținem o serie numită lângă Maclaurin:
,
Extinderea celor mai simple funcții (elementare) din seria Maclaurin:
Funcții exponențiale
, R=∞
Funcții trigonometrice ![]() , R=∞
, R=∞ ![]() , R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Funcția actgx nu se extinde în puteri ale lui x, deoarece ctg0=∞
Funcții hiperbolice
Funcții logaritmice
, -1
Seria binomială
![]() .
.
Exemplul nr. 1. Extindeți funcția într-o serie de puteri f(x)= 2X.
Soluţie. Să găsim valorile funcției și derivatele sale la X=0
f(x) = 2X, f( 0)
= 2 0
=1;
f"(x) = 2X ln2, f"( 0)
= 2 0
ln2= ln2;
f""(x) = 2X ln 2 2, f""( 0)
= 2 0
ln 2 2= ln 2 2;
…
f(n)(x) = 2X ln n 2, f(n)( 0)
= 2 0
ln n 2=ln n 2.
Înlocuind valorile obținute ale derivatelor în formula seriei Taylor, obținem:
Raza de convergență a acestei serii este egală cu infinitul, prin urmare această expansiune este valabilă pentru -∞<X<+∞.
Exemplul nr. 2. Scrieți seria Taylor în puteri ( X+4) pentru funcție f(x)= e X.
Soluţie. Aflarea derivatelor functiei e Xși valorile lor la punct X=-4.
f(x)= e X, f(-4)
= e -4
;
f"(x)= e X, f"(-4)
= e -4
;
f""(x)= e X, f""(-4)
= e -4
;
…
f(n)(x)= e X, f(n)( -4)
= e -4
.
Prin urmare, seria Taylor necesară a funcției are forma:
Această expansiune este valabilă și pentru -∞<X<+∞.
Exemplul nr. 3. Extindeți o funcție f(x)=ln Xîntr-o serie de puteri ( X- 1),
(adică în seria Taylor în vecinătatea punctului X=1).
Soluţie. Găsiți derivatele acestei funcții.
f(x)=lnx , , , ,
f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f (n) =(- 1) n-1 (n-1)!
Înlocuind aceste valori în formulă, obținem seria Taylor dorită:
Folosind testul lui d'Alembert, puteți verifica dacă seria converge la ½x-1½<1 . Действительно,
Seria converge dacă ½ X- 1½<1, т.е. при 0<X<2. При X=2 se obţine o serie alternativă care satisface condiţiile criteriului Leibniz. Când x=0 funcția nu este definită. Astfel, regiunea de convergență a seriei Taylor este intervalul semideschis (0;2).
Exemplul nr. 4. Extindeți funcția într-o serie de puteri. Exemplul nr. 5. Extindeți funcția într-o serie Maclaurin. cometariu
.
Această metodă se bazează pe teorema privind unicitatea expansiunii unei funcții într-o serie de puteri. Esența acestei teoreme este că în vecinătatea aceluiași punct nu se pot obține două serii de puteri diferite care ar converge către aceeași funcție, indiferent de modul în care este realizată expansiunea acesteia. Exemplul nr. 5a. Extindeți funcția într-o serie Maclaurin și indicați regiunea de convergență. Fracția 3/(1-3x) poate fi considerată ca fiind suma unei progresii geometrice infinit descrescătoare cu un numitor de 3x, dacă |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
Exemplul nr. 6. Extindeți funcția într-o serie Taylor în vecinătatea punctului x = 3. Exemplul nr. 7. Scrieți seria Taylor în puteri (x -1) ale funcției ln(x+2) . Exemplul nr. 8. Extindeți funcția f(x)=sin(πx/4) într-o serie Taylor în vecinătatea punctului x =2. Exemplul nr. 1. Calculați ln(3) la cel mai apropiat 0,01. Exemplul nr. 2. Calculați cu cel mai apropiat 0,0001. Exemplul nr. 3. Calculați integrala ∫ 0 1 4 sin (x) x până la 10 -5 . Exemplul nr. 4. Calculați integrala ∫ 0 1 4 e x 2 cu o precizie de 0,001. Extinderea unei funcții într-o serie Taylor, Maclaurin și Laurent pe un site pentru formarea abilităților practice. Această extindere în serie a unei funcții permite matematicienilor să estimeze valoarea aproximativă a funcției la un moment dat din domeniul său de definire. Este mult mai ușor să calculezi o astfel de valoare a funcției în comparație cu utilizarea tabelului Bredis, care este atât de irelevant în era tehnologiei informatice. A extinde o funcție într-o serie Taylor înseamnă a calcula coeficienții funcțiilor liniare ale acestei serii și a o scrie în forma corectă. Elevii confundă aceste două serii, neînțelegând care este cazul general și care este un caz special al celui de-al doilea. Să vă reamintim o dată pentru totdeauna că seria Maclaurin este un caz special al seriei Taylor, adică aceasta este seria Taylor, dar în punctul x = 0. Toate intrările scurte pentru extinderea funcțiilor binecunoscute, cum ar fi e^x, Sin(x), Cos(x) și altele, acestea sunt expansiuni de serie Taylor, dar la punctul 0 pentru argument. Pentru funcțiile unui argument complex, seria Laurent este cea mai comună problemă în TFCT, deoarece reprezintă o serie infinită cu două fețe. Este suma a două serii. Vă sugerăm să priviți un exemplu de descompunere direct pe site; acest lucru este foarte ușor de făcut făcând clic pe „Exemplu” cu orice număr și apoi pe butonul „Soluție”. Tocmai această extindere a unei funcții într-o serie care este asociată cu o serie majorizantă limitează funcția inițială într-o anumită regiune de-a lungul axei ordonatelor dacă variabila aparține regiunii absciselor. Analiza vectorială este comparată cu o altă disciplină interesantă din matematică. Deoarece fiecare termen trebuie examinat, procesul necesită destul de mult timp. Orice serie Taylor poate fi asociată cu o serie Maclaurin prin înlocuirea x0 cu zero, dar pentru o serie Maclaurin uneori nu este evident să reprezinte seria Taylor în sens invers. De parcă nu este necesar să se facă acest lucru în forma sa pură, este interesant pentru auto-dezvoltarea generală. Fiecare serie Laurent corespunde unei serii infinite de puteri cu două fețe în puteri întregi ale lui z-a, cu alte cuvinte, unei serii de același tip Taylor, dar ușor diferită în calculul coeficienților. Despre regiunea de convergență a seriei Laurent vom vorbi puțin mai târziu, după mai multe calcule teoretice. Ca și în secolul trecut, o extindere pas cu pas a unei funcții într-o serie cu greu poate fi realizată pur și simplu prin aducerea termenilor la un numitor comun, deoarece funcțiile din numitori sunt neliniare. Un calcul aproximativ al valorii funcționale este cerut de formularea problemelor. Gândiți-vă la faptul că atunci când argumentul unei serii Taylor este o variabilă liniară, atunci expansiunea are loc în mai mulți pași, dar imaginea este complet diferită atunci când argumentul funcției care se extinde este o funcție complexă sau neliniară, atunci procesul de reprezentarea unei astfel de funcții într-o serie de puteri este evidentă, întrucât, în acest fel, este ușor de calculat, deși o valoare aproximativă, în orice punct din regiunea de definire, cu o eroare minimă care are un efect redus asupra calculelor ulterioare. Acest lucru este valabil și pentru seria Maclaurin. când este necesar să se calculeze funcția la punctul zero. Cu toate acestea, seria Laurent în sine este reprezentată aici de o expansiune pe plan cu unități imaginare. De asemenea, soluția corectă a problemei în timpul procesului general nu va fi fără succes. Această abordare nu este cunoscută în matematică, dar există în mod obiectiv. Ca urmare, puteți ajunge la concluzia așa-numitelor submulțimi punctuale, iar în extinderea unei funcții într-o serie trebuie să utilizați metode cunoscute pentru acest proces, cum ar fi aplicarea teoriei derivatelor. Încă o dată suntem convinși că a avut dreptate profesorul, care și-a făcut presupunerile despre rezultatele calculelor post-computaționale. Să remarcăm că seria Taylor, obținută după toate canoanele matematicii, există și este definită pe întreaga axă numerică, totuși, dragi utilizatori ai serviciului de site, nu uitați de tipul funcției originale, deoarece se poate dovedi că inițial este necesar să se stabilească domeniul de definire al funcției, adică să se scrie și să se excludă de la analiza ulterioară acele puncte în care funcția nu este definită în domeniul numerelor reale. Ca să spunem așa, acest lucru vă va arăta eficiența în rezolvarea problemei. Construcția unei serii Maclaurin cu o valoare a argumentului zero nu va fi o excepție de la ceea ce s-a spus. Procesul de găsire a domeniului de definire a unei funcții nu a fost anulat și trebuie să abordați această operație matematică cu toată seriozitatea. În cazul unei serii Laurent care conține partea principală, parametrul „a” va fi numit punct singular izolat, iar seria Laurent va fi extinsă într-un inel - aceasta este intersecția zonelor de convergență a părților sale, prin urmare va urma teorema corespunzătoare. Dar nu totul este atât de complicat pe cât i-ar părea la prima vedere unui student fără experiență. După ce ați studiat seria Taylor, puteți înțelege cu ușurință seria Laurent - un caz generalizat pentru extinderea spațiului numerelor. Orice extindere în serie a unei funcții poate fi realizată numai într-un punct din domeniul de definire al funcției. Ar trebui luate în considerare proprietățile funcțiilor precum periodicitatea sau diferențiabilitatea infinită. De asemenea, vă sugerăm să utilizați tabelul de expansiuni gata făcute din seria Taylor ale funcțiilor elementare, deoarece o funcție poate fi reprezentată de până la zeci de serii de puteri diferite, așa cum se poate vedea folosind calculatorul nostru online. Seria online Maclaurin este la fel de ușor de determinat, dacă utilizați serviciul unic de site web, trebuie doar să introduceți funcția scrisă corectă și veți primi răspunsul prezentat în câteva secunde, este garantat că este exact și în o formă scrisă standard. Puteți copia rezultatul direct într-o copie curată pentru a fi transmisă profesorului. Ar fi corect să se determine mai întâi analiticitatea funcției în cauză în inele și apoi să se afirme fără ambiguitate că este extensibilă într-o serie Laurent în toate astfel de inele. Este important să nu pierdeți din vedere termenii seriei Laurent care conțin puteri negative. Concentrează-te pe asta cât mai mult posibil. Folosiți bine teorema lui Laurent privind extinderea unei funcții în puteri întregi. În teoria serielor funcționale, locul central este ocupat de secțiunea dedicată extinderii unei funcții într-o serie. Astfel, sarcina este stabilită: pentru o funcție dată
trebuie să găsim o astfel de serie de puteri care convergea pe un anumit interval şi suma lui era egală cu Această sarcină se numește problema extinderii unei funcții într-o serie de puteri. O condiție necesară pentru descompunerea unei funcții dintr-o serie de puteri este diferențiabilitatea sa de un număr infinit de ori - aceasta rezultă din proprietățile seriei de puteri convergente. Această condiție este îndeplinită, de regulă, pentru funcțiile elementare din domeniul lor de definire. Deci să presupunem că funcția Să presupunem că funcția Unde A 0 ,A 1 ,A 2 ,...,A P ,...
– coeficienți necunoscuți (încă). Să punem în egalitate (*) valoarea x = x 0 ,
atunci primim Să diferențiem seria de puteri (*) termen cu termen și crezând aici x = x 0 ,
primim Cu următoarea diferențiere obținem seria crezând x = x 0 ,
primim După P-diferențierea multiplă obținem Presupunând în ultima egalitate x = x 0 ,
primim Deci, se găsesc coeficienții înlocuind care în serie (*), obținem Seria rezultată se numește lângă Taylor
pentru functie
Astfel, am stabilit că dacă funcția poate fi extinsă într-o serie de puteri în puteri (x - x 0 ), atunci această expansiune este unică și seria rezultată este în mod necesar o serie Taylor. Rețineți că seria Taylor poate fi obținută pentru orice funcție care are derivate de orice ordin în punct x = x 0 .
Dar asta nu înseamnă că se poate plasa un semn egal între funcție și seria rezultată, adică. că suma seriei este egală cu funcția inițială. În primul rând, o astfel de egalitate poate avea sens numai în regiunea de convergență, iar seria Taylor obținută pentru funcție poate diverge și, în al doilea rând, dacă seria Taylor converge, atunci suma ei poate să nu coincidă cu funcția inițială. Să formulăm o declarație cu ajutorul căreia sarcina va fi rezolvată. Dacă funcţia
UndeR n (X)-termenul rămas al formulei Taylor – are forma (forma Lagrange) Unde
punctξ
se află între x și x 0 . Rețineți că există o diferență între seria Taylor și formula Taylor: formula Taylor este o sumă finită, i.e. P - număr fix. Amintiți-vă că suma seriei S(X)
poate fi definită ca limita unei succesiuni funcționale de sume parțiale S P (X)
la un anumit interval X: În conformitate cu aceasta, a extinde o funcție într-o serie Taylor înseamnă a găsi o serie astfel încât pentru oricare XX Să scriem formula lui Taylor sub forma unde observa asta Dacă Așa am dovedit criteriul de descompunere a unei funcții dintr-o serie Taylor.
Pentru functiaf(x) se extinde într-o serie Taylor, este necesar și suficient ca pe acest interval
Folosind criteriul formulat se poate obține suficientcondițiile de descompunere a unei funcții dintr-o serie Taylor.
Dacă învreo vecinătate a punctului x 0 valorile absolute ale tuturor derivatelor funcției sunt limitate la același număr M≥ 0, adică Din cele de mai sus rezultă algoritmextinderea funcției
f(X) în seria Taylorîn vecinătatea unui punct X 0 :
1.
Găsirea derivatelor de funcții f(X):
f(x), f’(x), f”(x), f’”(x), f (n) (X),… 2. Calculați valoarea funcției și valorile derivatelor sale la punctul X 0 f(x 0
), f’(x 0
), f”(x 0
), f’”(x 0
), f (n) (X 0
),…
3. Scriem în mod formal seria Taylor și găsim regiunea de convergență a seriei de puteri rezultate. 4. Verificam indeplinirea conditiilor suficiente, i.e. stabilim pentru care X din regiunea de convergență, restul termenului R n (X)
tinde spre zero ca Se numește extinderea funcțiilor într-o serie Taylor folosind acest algoritm extinderea unei funcții într-o serie Taylor prin definiție sau descompunere directă. Printre seriile funcționale, locul cel mai important este ocupat de seriile de putere. O serie de putere este o serie ai căror termeni sunt funcţii de putere dispuse în puteri întregi nenegative crescătoare X, A c0
, c 1
, c 2
, c n
- valori constante. Numerele c1
, c 2
, c n
- coeficienții termenilor seriei, c0
- membru gratuit. Termenii seriei de puteri sunt definiți pe întreaga linie numerică. Să ne familiarizăm cu conceptul zonele de convergenţă ale seriei de puteri.
Acesta este setul de valori ale unei variabile X, pentru care seria converge. Seriile de putere au o regiune de convergență destul de simplă. Pentru valori variabile reale X regiunea de convergență constă fie dintr-un punct, fie este un anumit interval (interval de convergență), fie coincide cu întreaga axă Bou
. Când înlocuiți valorile în seria de putere X= 0 va avea ca rezultat o serie de numere c0
+0+0+...+0+...
, care converge. Prin urmare, când X= 0 orice serie de puteri converge și, prin urmare, zona sa de convergență
nu poate fi setul gol. Structura regiunii de convergență a tuturor seriilor de puteri este aceeași. Se poate stabili folosind următoarea teoremă. Teorema 1 (teorema lui Abel). Dacă o serie de puteri converge la o anumită valoare X = X 0
, diferit de zero, atunci converge, și, în plus, absolut, pentru toate valorile |X| < |X 0
|
. Vă rugăm să rețineți: atât valoarea de pornire „X este zero”, cât și orice valoare a lui „X” care este comparată cu valoarea de pornire sunt luate modulo - fără a lua în considerare semnul. Consecinţă. Dacă seria de puteri diverge
la o oarecare valoare X = X 1
, apoi diverge pentru toate valorile |X| > |X 1
|
. După cum am aflat deja mai devreme, orice serie de puteri converge la valoare X= 0. Există serii de puteri care converg numai când X= 0 și diverge pentru alte valori X. Excluzând acest caz din considerare, presupunem că seria de puteri converge la o anumită valoare X = X 0
, diferit de zero. Apoi, conform teoremei lui Abel, converge în toate punctele intervalului ]-| X0
|, |X 0
|[
(un interval ale cărui limite din stânga și din dreapta sunt valorile x la care converge seria de puteri, luate cu semnul minus, respectiv cu semnul plus), simetric față de origine. Dacă seria de puteri diverge la o anumită valoare X = X 1
, apoi, pe baza corolarului teoremei lui Abel, ea diverge în toate punctele din afara segmentului [-| X1
|, |X 1
|]
. Rezultă că pentru orice serie de puteri există un interval simetric față de origine, numit interval de convergenta
, în fiecare punct al căruia seria converge, la limite poate converge, sau poate diverge, și nu neapărat în același timp, iar în afara segmentului seria diverge. Număr R se numește raza de convergență a seriei de puteri. În cazuri speciale intervalul de convergență al serii de puteri
poate degenera până la un punct (atunci seria converge numai atunci când X= 0 si se considera ca R= 0) sau reprezintă întreaga dreaptă numerică (atunci seria converge în toate punctele dreptei numerice și se presupune că ). Astfel, determinarea regiunii de convergență a unei serii de puteri constă în determinarea acesteia raza de convergenta
Rși studierea convergenței seriei la limitele intervalului de convergență (la ). Teorema 2. Dacă toți coeficienții unei serii de puteri, pornind de la o anumită, sunt diferiți de zero, atunci raza sa de convergență este egală cu limita la raportul valorilor absolute ale coeficienților membrilor comuni următori ai seriei. , adică Exemplul 1. Aflați regiunea de convergență a seriei de puteri Soluţie. Aici Folosind formula (28), găsim raza de convergență a acestei serii: Să studiem convergența seriei la capetele intervalului de convergență. Exemplul 13 arată că această serie converge la X= 1 și diverge la X= -1. În consecință, regiunea de convergență este semi-intervalul. Exemplul 2. Aflați regiunea de convergență a seriei de puteri Soluţie. Coeficienții seriei sunt pozitivi și Să găsim limita acestui raport, adică. raza de convergență a seriei de puteri: Să studiem convergența seriei la capetele intervalului. Înlocuirea valorilor X= -1/5 și X= 1/5 din acest rând dă: Prima dintre aceste serii converge (vezi Exemplul 5). Dar apoi, în virtutea teoremei din secțiunea „Convergență absolută”, a doua serie converge și ea, iar regiunea de convergență este segmentul Exemplul 3. Aflați regiunea de convergență a seriei de puteri Soluţie. Aici Folosind formula (28) găsim raza de convergență a seriei: Să studiem convergența seriei pentru valorile . Înlocuindu-le în această serie, obținem respectiv Ambele serii diverg deoarece condiția necesară pentru convergență nu este îndeplinită (termenii lor comuni nu tind să fie zero la ). Deci, la ambele capete ale intervalului de convergență, această serie diverge, iar regiunea de convergență este intervalul. Exemplul 5. Aflați regiunea de convergență a seriei de puteri Soluţie. Găsim relația unde , și Conform formulei (28), raza de convergență a acestei serii adică seria converge numai când X= 0 și diverge pentru alte valori X. Exemplele arată că la sfârșitul intervalului de convergență seria se comportă diferit. În exemplul 1, la un capăt al intervalului de convergență seria converge, iar la celălalt, ea diverge; în exemplul 2, converge la ambele capete; în exemplul 3, diverge la ambele capete. Formula pentru raza de convergență a unei serii de puteri se obține în ipoteza că toți coeficienții termenilor seriei, începând de la un anumit punct, sunt diferiți de zero. Prin urmare, utilizarea formulei (28) este permisă numai în aceste cazuri. Dacă această condiție este încălcată, atunci ar trebui căutată raza de convergență a seriei de puteri folosind semnul lui d'Alembert, sau, prin înlocuirea variabilei, transformarea seriei într-o formă în care condiția specificată este îndeplinită. Exemplul 6. Aflați intervalul de convergență al seriei de puteri Soluţie. Această serie nu conține termeni cu grade impare X. Prin urmare, transformăm seria, decorând . Apoi primim seria pentru a găsi raza de convergență căreia putem aplica formula (28). Deoarece , a , atunci raza de convergență a acestei serii Din egalitatea obținem, așadar, această serie converge către intervalul . Lasă pentru seria de putere raza de convergenţă R> 0, adică această serie converge pe intervalul . Apoi fiecare valoare X din intervalul de convergenţă corespunde unei anumite sume a seriei. Prin urmare, suma seriei de puteri este o funcție de X pe intervalul de convergenţă. Indicând-o prin f(X), putem scrie egalitatea înţelegându-l în sensul că suma seriei în fiecare punct X din intervalul de convergenţă este egală cu valoarea funcţiei f(X) în acest moment. În același sens, vom spune că seria de puteri (29) converge către funcție f(X) pe intervalul de convergenţă. În afara intervalului de convergență, egalitatea (30) nu are sens. Exemplul 7. Aflați suma seriei de puteri Soluţie. Aceasta este o serie geometrică pentru care A= 1, a q= X. Prin urmare, suma sa este o funcție este valabil doar pentru valori, deși funcția Se poate dovedi că suma seriei de puteri f(X) este continuă și diferențiabilă pe orice interval din intervalul de convergență, în special în orice punct al intervalului de convergență al seriei. Să prezentăm teoreme privind diferențierea termen cu termen și integrarea serii de puteri. Teorema 1. Seriile de puteri (30) în intervalul convergenței sale pot fi diferențiate termen cu termen de un număr nelimitat de ori, iar seriile de puteri rezultate au aceeași rază de convergență ca și seria inițială, iar sumele lor sunt, respectiv, egale cu . Teorema 2. Seria de putere (30) poate fi integrată termen cu termen de un număr nelimitat de ori în intervalul de la 0 la X, dacă , și seria de puteri rezultată au aceeași rază de convergență ca și seria originală, iar sumele lor sunt egale în mod corespunzător Să fie dată funcția f(X), care trebuie extins într-o serie de puteri, i.e. reprezintă sub forma (30): Sarcina este de a determina coeficienții ……………………………………………….. (31) Presupunând în egalități (30) și (31) X= 0, găsim Înlocuind expresiile găsite în egalitatea (30), obținem Să găsim extinderea seriei Maclaurin a unor funcții elementare. Exemplul 8. Extindeți funcția într-o serie Maclaurin Soluţie. Derivatele acestei funcții coincid cu funcția însăși: Prin urmare, când X= 0 avem Înlocuind aceste valori în formula (32), obținem expansiunea dorită: Această serie converge pe întreaga dreaptă numerică (raza sa de convergență).
Soluţie. În expansiunea (1) înlocuim x cu -x 2, obținem:
, -∞
Soluţie. Avem
Folosind formula (4), putem scrie:
înlocuind –x în loc de x în formulă, obținem:
De aici găsim: ln(1+x)-ln(1-x) = -
Deschidem parantezele, rearanjam termenii seriei și aducem termeni similari, obținem
. Această serie converge în intervalul (-1;1), deoarece se obține din două serii, fiecare dintre acestea convergând în acest interval.
Formulele (1)-(5) pot fi, de asemenea, utilizate pentru a extinde funcțiile corespunzătoare într-o serie Taylor, de exemplu. pentru extinderea funcțiilor în puteri întregi pozitive ( Ha). Pentru a face acest lucru, este necesar să efectuați astfel de transformări identice asupra unei anumite funcții pentru a obține una dintre funcțiile (1)-(5), în care în schimb X costă k( Ha) m , unde k este un număr constant, m este un întreg pozitiv. Este adesea convenabil să faceți o schimbare a variabilei t=Hași extindeți funcția rezultată în raport cu t în seria Maclaurin.
Soluţie. Mai întâi găsim 1-x-6x 2 =(1-3x)(1+2x) , .
la elementar:
cu regiunea de convergenţă |x|< 1/3.
Soluţie. Această problemă poate fi rezolvată, ca și înainte, folosind definiția seriei Taylor, pentru care trebuie să găsim derivatele funcției și valorile acestora la X=3. Cu toate acestea, va fi mai ușor să utilizați extinderea existentă (5):
=
Seria rezultată converge la sau –3
Soluţie.
Seria converge la , sau -2< x < 5.
Soluţie. Să facem înlocuirea t=x-2:
Folosind expansiunea (3), în care înlocuim π / 4 t în locul lui x, obținem:
Seria rezultată converge către funcția dată la -∞< π / 4 t<+∞, т.е. при (-∞
, (-∞Calcule aproximative folosind seria de puteri
Seriile de putere sunt utilizate pe scară largă în calcule aproximative. Cu ajutorul lor, puteți calcula valorile rădăcinilor, funcțiilor trigonometrice, logaritmilor numerelor și integralelor definite cu o precizie dată. Seriile sunt de asemenea folosite la integrarea ecuațiilor diferențiale.
Luați în considerare expansiunea unei funcții într-o serie de puteri:
Pentru a calcula valoarea aproximativă a unei funcții într-un punct dat X, aparținând regiunii de convergență a seriei indicate, primele sunt lăsate în extinderea acesteia n membri ( n– un număr finit), iar termenii rămași sunt eliminați:
Pentru a estima eroarea valorii aproximative obținute, este necesar să se estimeze restul aruncat rn (x) . Pentru a face acest lucru, utilizați următoarele tehnici:
Soluţie. Să folosim expansiunea unde x=1/2 (vezi exemplul 5 din subiectul anterior):
Să verificăm dacă putem elimina restul după primii trei termeni ai expansiunii; pentru a face acest lucru, îl vom evalua folosind suma unei progresii geometrice infinit descrescătoare:
Deci, putem arunca acest rest și obținem
Soluţie. Să folosim seria binomială. Deoarece 5 3 este cubul unui număr întreg cel mai apropiat de 130, este recomandabil să se reprezinte numărul 130 ca 130 = 5 3 +5. 
deoarece deja cel de-al patrulea termen al seriei alternative rezultate care satisface criteriul Leibniz este mai mic decât precizia cerută:
, astfel încât acesta și termenii care îi urmează pot fi eliminate.
Multe integrale definite sau improprie practic necesare nu pot fi calculate folosind formula Newton-Leibniz, deoarece aplicarea acesteia este asociată cu găsirea antiderivatei, care de multe ori nu are expresie în funcții elementare. De asemenea, se întâmplă că găsirea unui antiderivat este posibilă, dar necesită o forță de muncă inutilă. Cu toate acestea, dacă funcția integrand este extinsă într-o serie de puteri, iar limitele integrării aparțin intervalului de convergență al acestei serii, atunci este posibil un calcul aproximativ al integralei cu o precizie predeterminată.
Soluţie. Integrala nedefinită corespunzătoare nu poate fi exprimată în funcții elementare, adică. reprezintă o „integrală nepermanentă”. Formula Newton-Leibniz nu poate fi aplicată aici. Să calculăm integrala aproximativ.
Împărțirea termen cu termen a seriei pentru păcat X pe X, primim: 
Integrând această serie termen cu termen (acest lucru este posibil, întrucât limitele de integrare aparțin intervalului de convergență al acestei serii), obținem:
Deoarece seria rezultată satisface condițiile lui Leibniz și este suficient să luăm suma primilor doi termeni pentru a obține valoarea dorită cu o precizie dată.
Astfel, găsim  .
.
Soluţie.

![]() . Să verificăm dacă putem elimina restul după al doilea termen al seriei rezultate.
. Să verificăm dacă putem elimina restul după al doilea termen al seriei rezultate.
0,0001<0.001. Следовательно,  .
. ,
acestea.
,
acestea. =
..
=
..
 are derivate de orice ordin. Este posibil să o extindem într-o serie de putere? Dacă da, cum putem găsi această serie? A doua parte a problemei este mai ușor de rezolvat, așa că să începem cu ea.
are derivate de orice ordin. Este posibil să o extindem într-o serie de putere? Dacă da, cum putem găsi această serie? A doua parte a problemei este mai ușor de rezolvat, așa că să începem cu ea. poate fi reprezentat ca suma unei serii de puteri convergente în intervalul care conține punctul X 0 :
poate fi reprezentat ca suma unei serii de puteri convergente în intervalul care conține punctul X 0 :
 =
..
(*)
=
..
(*) .
. =
..
=
..
 .
. =
..
=
..
 , Unde
, Unde  .
. , Unde
, Unde
 ,
,
 ,
,
 ,
…,
,
…,
 ,….,
,…., .
.
3.2. Condiții suficiente pentru descompunerea unei funcții dintr-o serie Taylor
 într-o vecinătate a punctului x 0 are derivate până la (n+
1) de ordin inclusiv, atunci în acest cartier avemformulă
Taylor
într-o vecinătate a punctului x 0 are derivate până la (n+
1) de ordin inclusiv, atunci în acest cartier avemformulă
Taylor

 .
.
 definește eroarea pe care o obținem, înlocuiți funcția f(X)
polinom S n (X).
definește eroarea pe care o obținem, înlocuiți funcția f(X)
polinom S n (X).
 , Acea
, Acea  ,acestea. funcția este extinsă într-o serie Taylor. Viceversa, dacă
,acestea. funcția este extinsă într-o serie Taylor. Viceversa, dacă  , Acea
, Acea  .
. , UndeR n (X) este termenul rămas al seriei Taylor.
, UndeR n (X) este termenul rămas al seriei Taylor. , To în această vecinătate funcția se extinde într-o serie Taylor.
, To în această vecinătate funcția se extinde într-o serie Taylor. sau
sau
 .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]() :
:![]()
![]() ,
,![]()
![]()
![]()
Suma seriei de putere. Diferențierea și integrarea serii de puteri
![]()
![]() . O serie converge dacă , și este intervalul său de convergență. Prin urmare egalitate
. O serie converge dacă , și este intervalul său de convergență. Prin urmare egalitate![]()
![]() definit pentru toate valorile X, cu exceptia X= 1.
definit pentru toate valorile X, cu exceptia X= 1.
Extinderea funcțiilor în serii de puteri
![]() rândul (30). Pentru a face acest lucru, diferențiind egalitatea (30) termen cu termen, găsim în mod constant:
rândul (30). Pentru a face acest lucru, diferențiind egalitatea (30) termen cu termen, găsim în mod constant:![]()
![]()

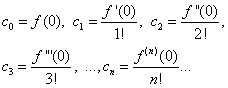
 (32)
(32)
![]() (33)
(33)

