Taylor sorozat bővítése cos. A függvények hatványsorokká bővítése
16.1. Az elemi függvények kiterjesztése Taylor sorozatba ill
Maclaurin
Mutassuk meg, hogy ha egy halmazon tetszőleges függvény van definiálva  , a pont környékén
, a pont környékén  sok deriváltja van, és egy hatványsor összege:
sok deriváltja van, és egy hatványsor összege:
akkor megtalálhatja ennek a sorozatnak az együtthatóit.
Helyettesítsük be egy hatványsorba  . Akkor
. Akkor  .
.
Keressük meg a függvény első deriváltját  :
:
Nál nél  :
: .
.
A második származékra a következőket kapjuk:
Nál nél  :
: .
.
Ennek az eljárásnak a folytatása n ha egyszer megkapjuk:  .
.
Így a következő alakú hatványsort kaptuk:


 ,
,
amelyet úgy hívnak Taylor mellett funkcióhoz  pont közelében
pont közelében  .
.
A Taylor-sorozat speciális esete az Maclaurin sorozat nál nél  :
:



A Taylor (Maclaurin) sorozat fennmaradó részét a fő sorozat eldobásával kapjuk meg n első tagok, és jelölése:  . Aztán a függvény
. Aztán a függvény  összegként írható fel n sorozat első tagjai
összegként írható fel n sorozat első tagjai  és a maradék
és a maradék  :,
:,
 .
.
A maradék általában  különböző képletekben kifejezve.
különböző képletekben kifejezve.
Az egyik Lagrange formában van:
 , Ahol
, Ahol  .
. .
.
Vegye figyelembe, hogy a gyakorlatban a Maclaurin sorozatot gyakrabban használják. Így a függvény írásához  hatványsor összeg formájában szükséges:
hatványsor összeg formájában szükséges:
1) keresse meg a Maclaurin (Taylor) sorozat együtthatóit;
2) keresse meg a kapott hatványsorok konvergenciatartományát;
3) bizonyítsuk be, hogy ez a sorozat a függvényhez konvergál  .
.
Tétel1
(a Maclaurin-sorok konvergenciájának szükséges és elégséges feltétele). Legyen a sorozat konvergencia sugara  . Annak érdekében, hogy ez a sorozat az intervallumban konvergáljon
. Annak érdekében, hogy ez a sorozat az intervallumban konvergáljon  funkcionálni, működtetni
funkcionálni, működtetni  szükséges és elegendő a feltétel teljesüléséhez:
szükséges és elegendő a feltétel teljesüléséhez:  a megadott intervallumban.
a megadott intervallumban.
2. tétel. Ha a függvény bármely rendjének deriváltjai  valamilyen intervallumban
valamilyen intervallumban  abszolút értékben ugyanarra a számra korlátozódik M, vagyis
abszolút értékben ugyanarra a számra korlátozódik M, vagyis  , akkor ebben az intervallumban a függvény
, akkor ebben az intervallumban a függvény  Maclaurin sorozattá bővíthető.
Maclaurin sorozattá bővíthető.
Példa1
.
Bővítse ki egy Taylor-sorozatot a lényeg körül  funkció.
funkció.
Megoldás.
 .
.
 ,;
,;
 ,
, ;
;
 ,
, ;
;
 ,
,
.......................................................................................................................................
 ,
, ;
;
Konvergencia régió  .
.
Példa2
.
Funkció kibontása  egy Taylor-sorozatban egy pont körül
egy Taylor-sorozatban egy pont körül  .
.
Megoldás:
Keresse meg a függvény és származékainak értékét itt  .
.
 ,
, ;
;
 ,
, ;
;
...........……………………………
 ,
, .
.
Tegyük sorba ezeket az értékeket. Kapunk:
vagy  .
.
Keressük meg ennek a sorozatnak a konvergencia tartományát. D'Alembert tesztje szerint egy sorozat konvergál, ha
 .
.
Ezért bármely  ez a határ 1-nél kisebb, ezért a sorozatok konvergenciatartománya a következő lesz:
ez a határ 1-nél kisebb, ezért a sorozatok konvergenciatartománya a következő lesz:  .
.
Nézzünk néhány példát az alapvető elemi függvények Maclaurin-soros kiterjesztésére. Emlékezzünk vissza, hogy a Maclaurin sorozat:


 .
.
az intervallumhoz konvergál  funkcionálni, működtetni
funkcionálni, működtetni  .
.
Vegye figyelembe, hogy egy függvény sorozattá bővítéséhez szükséges:
a) keresse meg a Maclaurin-sor együtthatóit ehhez a függvényhez;
b) kiszámítja a kapott sorozat konvergencia sugarát;
c) bizonyítsa be, hogy a kapott sorozat a függvényhez konvergál  .
.
3. példa Vegye figyelembe a funkciót  .
.
Megoldás.
Számítsuk ki a függvény értékét és deriváltjait at  .
.
Ekkor a sorozat numerikus együtthatói a következőképpen alakulnak:
bárkinek n. Helyettesítsük be a talált együtthatókat a Maclaurin-sorba, és kapjuk: 
Határozzuk meg az eredményül kapott sorozatok konvergencia sugarát, nevezetesen:
 .
.
Ezért a sorozat az intervallumhoz konvergál  .
.
Ez a sorozat a függvényhez konvergál  bármilyen értékre
bármilyen értékre  , mert bármilyen intervallumon
, mert bármilyen intervallumon  funkció
funkció  abszolút értékű származékai pedig korlátozottak
abszolút értékű származékai pedig korlátozottak  .
.
Példa4
.
Vegye figyelembe a funkciót  .
.
Megoldás.
 :
:

Könnyen belátható, hogy az egyenletes sorrendű származékok  , és a származékok páratlan sorrendűek. Helyettesítsük be a talált együtthatókat a Maclaurin-sorba, és kapjuk meg a kiterjesztést:
, és a származékok páratlan sorrendűek. Helyettesítsük be a talált együtthatókat a Maclaurin-sorba, és kapjuk meg a kiterjesztést:
Határozzuk meg ennek a sorozatnak a konvergencia intervallumát. D'Alembert jele szerint:
bárkinek  . Ezért a sorozat az intervallumhoz konvergál
. Ezért a sorozat az intervallumhoz konvergál  .
.
Ez a sorozat a függvényhez konvergál  , mert minden származéka az egységre korlátozódik.
, mert minden származéka az egységre korlátozódik.
Példa5
.
 .
.
Megoldás.
Határozzuk meg a függvény és származékainak értékét at  :
:

Így ennek a sorozatnak az együtthatói:  És
És  , ennélfogva:
, ennélfogva:
Az előző sorhoz hasonlóan a konvergencia területe  . A sorozat a függvényhez konvergál
. A sorozat a függvényhez konvergál  , mert minden származéka az egységre korlátozódik.
, mert minden származéka az egységre korlátozódik.
Felhívjuk figyelmét, hogy a funkció  páratlan és soros bővítés páratlan hatványokban, függvény
páratlan és soros bővítés páratlan hatványokban, függvény  – páros és sorozattá bővítés páros hatványokban.
– páros és sorozattá bővítés páros hatványokban.
Példa6
.
Binomiális sorozat:  .
.
Megoldás.
Határozzuk meg a függvény és származékainak értékét at  :
:

Ebből látható, hogy:

Helyettesítsük be ezeket az együttható értékeket a Maclaurin sorozatba, és kapjuk meg ennek a függvénynek a hatványsorba való kiterjesztését:
Nézzük meg ennek a sorozatnak a konvergencia sugarát:

Ezért a sorozat az intervallumhoz konvergál  . A határpontokon a
. A határpontokon a  És
És  egy sorozat a kitevőtől függően konvergálhat vagy nem
egy sorozat a kitevőtől függően konvergálhat vagy nem  .
.
A vizsgált sorozatok az intervallumhoz konvergálnak  funkcionálni, működtetni
funkcionálni, működtetni  , vagyis a sorozat összege
, vagyis a sorozat összege  nál nél
nál nél  .
.
Példa7
.
Bővítsük ki a függvényt a Maclaurin sorozatban  .
.
Megoldás.
Ha ezt a függvényt sorozattá kívánjuk bővíteni, az at binomiális sorozatot használjuk  . Kapunk:
. Kapunk: 
A hatványsorok tulajdonsága alapján (egy hatványsor integrálható a konvergenciájának tartományába) megtaláljuk ennek a sorozatnak a bal és jobb oldalának integrálját:
Keressük meg ennek a sorozatnak a konvergencia területét:  ,
,
vagyis ennek a sorozatnak a konvergencia területe az intervallum  . Határozzuk meg a sorozatok konvergenciáját az intervallum végén. Nál nél
. Határozzuk meg a sorozatok konvergenciáját az intervallum végén. Nál nél 
 . Ez a sorozat harmonikus sorozat, vagyis szétválik. Nál nél
. Ez a sorozat harmonikus sorozat, vagyis szétválik. Nál nél  közös tagú számsort kapunk
közös tagú számsort kapunk  .
.
A sorozat Leibniz tesztje szerint konvergál. Így ennek a sorozatnak a konvergencia tartománya az intervallum  .
.
16.2. Hatványsorok alkalmazása közelítő számításokban
A közelítő számításokban a hatványsorok rendkívül fontos szerepet játszanak. Segítségükkel trigonometrikus függvénytáblázatokat, logaritmustáblázatokat, más függvények értéktáblázatait állítottuk össze, amelyeket különféle ismeretterületeken használnak, például a valószínűségszámításban és a matematikai statisztikában. Ezen túlmenően a függvények hatványsorokká történő kiterjesztése hasznos az elméleti tanulmányozásukhoz. A fő probléma hatványsorok közelítő számításokban való használatakor az a hiba becslése, amikor egy sorozat összegét az első sor összegével helyettesítjük. n tagjai.
Nézzünk két esetet:
a funkciót jel-alternáló sorozattá bővítjük;
a függvény egy állandó előjel sorozatává bővül.
Számítás váltakozó sorozatok használatával
Legyen a függvény  váltakozó hatványsorozattá bővült. Majd amikor ezt a függvényt egy adott értékre számítja ki
váltakozó hatványsorozattá bővült. Majd amikor ezt a függvényt egy adott értékre számítja ki  számsort kapunk, amelyre a Leibniz-kritériumot alkalmazhatjuk. Ennek a kritériumnak megfelelően, ha egy sorozat összegét az első sorozat összegével helyettesítjük n akkor az abszolút hiba nem haladja meg a sorozat többi részének első tagját, azaz:
számsort kapunk, amelyre a Leibniz-kritériumot alkalmazhatjuk. Ennek a kritériumnak megfelelően, ha egy sorozat összegét az első sorozat összegével helyettesítjük n akkor az abszolút hiba nem haladja meg a sorozat többi részének első tagját, azaz:  .
.
Példa8
.
Kiszámítja  0,0001 pontossággal.
0,0001 pontossággal.
Megoldás.
Ehhez a Maclaurin sorozatot fogjuk használni  , a radiánban megadott szögértéket helyettesítve:
, a radiánban megadott szögértéket helyettesítve:

Ha adott pontossággal összehasonlítjuk a sorozat első és második tagját, akkor: .
A bővítés harmadik időszaka:
kisebb, mint a megadott számítási pontosság. Ezért számolni  elég a sorozat két tagját elhagyni, azaz
elég a sorozat két tagját elhagyni, azaz
 .
.
És így  .
.
Példa9
.
Kiszámítja  0,001 pontossággal.
0,001 pontossággal.
Megoldás.
A binomiális sorozat képletét fogjuk használni. Ehhez írjunk  mint:
mint:  .
.
Ebben a kifejezésben  ,
,

Hasonlítsuk össze a sorozat egyes feltételeit a megadott pontossággal. Ez egyértelmű  . Ezért számolni
. Ezért számolni  elég a sorozat három tagját elhagyni.
elég a sorozat három tagját elhagyni.
 vagy
vagy  .
.
Számítás pozitív sorozatok felhasználásával
Példa10
.
Számítsa ki a számot  0,001 pontossággal.
0,001 pontossággal.
Megoldás.
Egy sorban egy funkcióhoz  helyettesítsük
helyettesítsük  . Kapunk:
. Kapunk:

Becsüljük meg azt a hibát, amely akkor keletkezik, ha egy sorozat összegét az első összegére cseréljük  tagjai. Írjuk fel a nyilvánvaló egyenlőtlenséget:
tagjai. Írjuk fel a nyilvánvaló egyenlőtlenséget:
vagyis 2< <3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
<3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
 ,
, .
.
A probléma szerint meg kell találni núgy, hogy a következő egyenlőtlenség teljesüljön:  vagy
vagy  .
.
Könnyű ellenőrizni, hogy mikor n= 6: .
.
Ennélfogva,  .
.
Példa11
.
Kiszámítja  0,0001 pontossággal.
0,0001 pontossággal.
Megoldás.
Vegye figyelembe, hogy a logaritmusok kiszámításához használhatunk egy sorozatot a függvényhez  , de ez a sorozat nagyon lassan konvergál és az adott pontosság eléréséhez 9999 tagot kellene felvenni! Ezért a logaritmusok kiszámításához általában a függvény sorozatát használják
, de ez a sorozat nagyon lassan konvergál és az adott pontosság eléréséhez 9999 tagot kellene felvenni! Ezért a logaritmusok kiszámításához általában a függvény sorozatát használják  , amely az intervallumhoz konvergál
, amely az intervallumhoz konvergál  .
.
Számoljunk  használja ezt a sorozatot. Hadd
használja ezt a sorozatot. Hadd  , Akkor
, Akkor  .
.
Ennélfogva,  ,
,
Számítás céljából  adott pontossággal vegyük az első négy tag összegét:
adott pontossággal vegyük az első négy tag összegét:  .
.
A sorozat többi része  dobjuk el. Becsüljük meg a hibát. Ez nyilvánvaló
dobjuk el. Becsüljük meg a hibát. Ez nyilvánvaló 
vagy  .
.

Így a számításhoz használt sorozatban elég volt csak az első négy tagot venni a függvényhez a 9999 helyett.  .
.
Öndiagnosztikai kérdések
1. Mi az a Taylor sorozat?
2. Milyen formában volt a Maclaurin sorozat?
3. Fogalmazzon meg egy tételt egy Taylor-sor függvényének kiterjesztésére!
4. Írja le a fő függvények Maclaurin sorozatának bővítését!
5. Jelölje meg a vizsgált sorozatok konvergenciaterületeit!
6. Hogyan becsüljük meg a hibát a hatványsorokat használó közelítő számításokban?
Ha az f(x) függvénynek egy adott a pontot tartalmazó intervallumon minden rendjének deriváltja van, akkor a Taylor-képlet alkalmazható rá:
,
Ahol r n– a sorozat úgynevezett maradéktagja vagy maradéka, a Lagrange-képlet segítségével becsülhető meg:
, ahol az x szám x és a között van.
A függvények bevitelének szabályai:
Ha valamilyen értékért x r n→0 at n→∞, akkor a határértékben a Taylor-képlet erre az értékre konvergenssé válik Taylor sorozat:
,
Így az f(x) függvény Taylor-sorrá bővíthető a vizsgált x pontban, ha:
1) minden rendből származékai vannak;
2) a megszerkesztett sorozat ezen a ponton konvergál.
Ha a = 0, akkor az úgynevezett sorozatot kapjuk Maclaurin közelében:
,
A Maclaurin sorozat legegyszerűbb (elemi) függvényeinek bővítése:
Exponenciális függvények
, R=∞
Trigonometrikus függvények ![]() , R=∞
, R=∞ ![]() , R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Az actgx függvény nem bővül x hatványaiban, mert ctg0=∞
Hiperbolikus függvények
Logaritmikus függvények
, -1
Binomiális sorozat
![]() .
.
1. számú példa. Bontsa ki a függvényt hatványsorokká f(x)= 2x.
Megoldás. Keressük meg a függvény és deriváltjainak értékeit itt x=0
f(x) = 2x, f( 0)
= 2 0
=1;
f"(x) = 2x ln2, f"( 0)
= 2 0
ln2=ln2;
f""(x) = 2x 22-ben, f""( 0)
= 2 0
ln 2 2= ln 2 2;
…
f(n)(x) = 2x ln n 2, f(n)( 0)
= 2 0
ln n 2=ln n 2.
A származékok kapott értékeit behelyettesítve a Taylor-sor képletébe, a következőket kapjuk:
Ennek a sorozatnak a konvergencia sugara egyenlő a végtelennel, ezért ez a kiterjesztés érvényes -∞<x<+∞.
2. példa. Írd fel a Taylor sorozatot hatványokkal ( x+4) funkcióhoz f(x)= e x.
Megoldás. Az e függvény deriváltjainak megkeresése xés értékeiket a ponton x=-4.
f(x)= e x, f(-4)
= e -4
;
f"(x)= e x, f"(-4)
= e -4
;
f""(x)= e x, f""(-4)
= e -4
;
…
f(n)(x)= e x, f(n)( -4)
= e -4
.
Ezért a függvény szükséges Taylor sorozatának alakja a következő:
Ez a bővítés a -∞-re is érvényes<x<+∞.
3. példa. Funkció kibontása f(x)=ln x erők sorozatában ( X- 1),
(azaz a Taylor sorozatban a pont közelében x=1).
Megoldás. Keresse meg ennek a függvénynek a deriváltjait.
f(x)=lnx , , , ,
f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f (n) =(- 1) n-1 (n-1)!
Ezeket az értékeket behelyettesítve a képletbe, megkapjuk a kívánt Taylor sorozatot:
A d'Alembert-teszt segítségével ellenőrizheti, hogy a sorozat ½x-1½ konvergál.<1 . Действительно,
A sorozat akkor konvergál, ha ½ X- 1½<1, т.е. при 0<x<2. При x=2 kapunk egy váltakozó sorozatot, amely kielégíti a Leibniz-kritérium feltételeit. Ha x=0, a függvény nincs definiálva. Így a Taylor-sor konvergenciatartománya a félig nyitott intervallum (0;2]).
4. számú példa. Bontsa ki a függvényt hatványsorokká. 5. számú példa. Bővítse ki a függvényt Maclaurin sorozattá. Megjegyzés
.
Ez a módszer egy hatványsorbeli függvény kiterjesztésének egyediségére vonatkozó tételen alapul. Ennek a tételnek az a lényege, hogy ugyanazon pont szomszédságában nem kaphatunk két különböző hatványsort, amely ugyanahhoz a függvényhez konvergálna, függetlenül attól, hogy a kiterjesztését hogyan hajtjuk végre. 5a. példa. Bontsa ki a függvényt egy Maclaurin sorozatban, és jelölje meg a konvergencia tartományát. A 3/(1-3x) tört egy 3x-os nevezővel végtelenül csökkenő geometriai progresszió összegének tekinthető, ha |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
6. számú példa. Bontsa ki a függvényt Taylor sorozattá az x = 3 pont közelében. 7. számú példa. Írja fel az ln(x+2) függvény Taylor-sorát hatványaiban (x -1). 8. számú példa. Bontsa ki az f(x)=sin(πx/4) függvényt Taylor-sorba az x =2 pont közelében. 1. számú példa. Számítsa ki az ln(3)-t 0,01 pontossággal. 2. példa. Számítsa ki 0,0001 pontossággal. 3. példa. Számítsa ki a ∫ 0 1 4 sin (x) x integrált 10 -5 pontossággal. 4. számú példa. Számítsa ki a ∫ 0 1 4 e x 2 integrált 0,001 pontossággal. Egy funkció kiterjesztése Taylor, Maclaurin és Laurent sorozatra a gyakorlati ismeretek képzésére szolgáló oldalon. Egy függvénynek ez a sorozatbővítése lehetővé teszi a matematikusok számára, hogy megbecsüljék a függvény közelítő értékét a definíciós tartomány egy bizonyos pontján. Sokkal könnyebb kiszámítani egy ilyen függvényértéket, mint a számítástechnika korában annyira irreleváns Bredis-táblázat használatával. Ha egy függvényt Taylor-sorrá bővítünk, akkor ennek a sorozatnak a lineáris függvényeinek együtthatóit kell kiszámítani és a megfelelő formában írni. A tanulók összekeverik ezt a két sorozatot, nem értik, mi az általános és mi a speciális eset a másodiknál. Emlékeztessünk egyszer s mindenkorra, hogy a Maclaurin sorozat a Taylor sorozat speciális esete, vagyis ez a Taylor sorozat, de az x = 0 ponton. Minden rövid bejegyzés a jól ismert függvények bővítésére, mint például az e^x, Sin(x), Cos(x) és mások, ezek Taylor sorozat kiterjesztések, de az argumentum 0 pontja. Egy összetett argumentum függvényeinél a Laurent-sor a leggyakoribb probléma a TFCT-ben, mivel ez egy kétoldalú végtelen sorozatot képvisel. Ez két sorozat összege. Javasoljuk, hogy nézzen meg egy példát a dekompozícióra közvetlenül a webhelyen; ezt nagyon egyszerűen megteheti, ha rákattint a „Példa” tetszőleges számmal, majd a „Megoldás” gombra. Pontosan a függvénynek ez a sorozattá való kiterjesztése, amely egy majorizáló sorozathoz kapcsolódik, korlátozza az eredeti függvényt egy bizonyos tartományban az ordináta tengely mentén, ha a változó az abszcissza tartományba tartozik. A vektoranalízist egy másik érdekes matematikai tudományághoz hasonlítják. Mivel minden kifejezést meg kell vizsgálni, a folyamat meglehetősen sok időt vesz igénybe. Bármely Taylor-sorozat társítható egy Maclaurin-sorozathoz, ha x0-t nullára cserélünk, de egy Maclaurin-sorozat esetében néha nem nyilvánvaló, hogy a Taylor-sorozatot fordítva ábrázoljuk. Mintha ezt nem tiszta formájában kell megtenni, általános önfejlesztés szempontjából érdekes. Minden Laurent-sorozat egy kétoldalas végtelen hatványsornak felel meg z-a egész hatványaiban, más szóval egy ugyanolyan Taylor-típusú sorozatnak, amely az együtthatók számításában kissé eltérő. A Laurent-sorozat konvergencia régiójáról kicsit később, több elméleti számítás után beszélünk. A múlt századhoz hasonlóan egy függvény lépésről lépésre sorozattá való bővítése aligha valósítható meg egyszerűen a kifejezések közös nevezőre hozásával, mivel a nevezőkben lévő függvények nemlineárisak. A funkcionális érték közelítő számítását a feladatok megfogalmazása teszi szükségessé. Gondoljunk csak arra, hogy ha egy Taylor-sor argumentuma lineáris változó, akkor a bővítés több lépésben történik, de teljesen más a kép, ha a bővítendő függvény argumentuma összetett vagy nemlineáris függvény, akkor a folyamat Egy ilyen függvény hatványsorban való ábrázolása kézenfekvő, mivel így könnyen kiszámítható, bár közelítő érték a definíciós tartomány bármely pontján, minimális hibával, aminek nincs hatása a további számításokra. Ez vonatkozik a Maclaurin sorozatra is. amikor a függvényt a nullapontban kell kiszámítani. Magát a Laurent-sorozatot azonban itt a síkon egy képzeletbeli egységekkel való bővítés képviseli. Ezenkívül a probléma helyes megoldása a teljes folyamat során nem marad sikertelenül. Ez a megközelítés nem ismert a matematikában, de objektíve létezik. Ennek eredményeként az úgynevezett pontszerű részhalmazokra juthatunk, és egy függvény sorozatban történő bővítésekor ehhez a folyamathoz ismert módszereket kell alkalmazni, mint például a derivált elmélet alkalmazása. Ismét megbizonyosodtunk arról, hogy igaza volt a tanárnak, aki az utószámítási eredményeket illetően feltételezte. Vegyük észre, hogy a matematika összes kánonja szerint kapott Taylor sorozat létezik és a teljes numerikus tengelyen definiálva van, azonban kedves oldalszolgáltatás használók ne felejtsék el az eredeti függvény típusát, mert kiderülhet hogy kezdetben meg kell határozni a függvény definíciós tartományát, azaz fel kell írni és kizárni a további vizsgálatból azokat a pontokat, ahol a függvény nincs definiálva a valós számok tartományában. Úgymond ez megmutatja a problémamegoldás hatékonyságát. A nulla argumentumértékű Maclaurin-sorozat felépítése sem lesz kivétel az elmondottak alól. A függvény definíciós tartományának megtalálásának folyamata nem szakadt meg, és ezt a matematikai műveletet teljes komolysággal kell megközelíteni. A főrészt tartalmazó Laurent-sorok esetében az „a” paramétert izolált szinguláris pontnak nevezzük, a Laurent-sort pedig gyűrűben bővítjük – ez a részei konvergenciaterületeinek metszéspontja, tehát a megfelelő tétel következik. De nem minden olyan bonyolult, mint amilyennek első pillantásra tűnhet egy tapasztalatlan diák számára. A Taylor sorozat tanulmányozása után könnyen megértheti a Laurent sorozatot - egy általános esetet a számterek bővítésére. Egy függvény bármilyen sorozatbővítése csak a függvény definíciós tartományának egy pontján hajtható végre. Figyelembe kell venni a függvények olyan tulajdonságait, mint a periodicitás vagy a végtelen differenciálhatóság. Javasoljuk továbbá, hogy használja az elemi függvények kész Taylor-sorozat-kiterjesztéseinek táblázatát, mivel egy függvény akár több tucat különböző hatványsorral is ábrázolható, amint az online számológépünk használatával is látható. Az online Maclaurin sorozat meghatározása olyan egyszerű, mint a torta, ha az egyedülálló weboldal szolgáltatást használja, csak a megfelelő írásos funkciót kell megadnia, és pillanatok alatt megkapja a bemutatott választ, garantáltan pontos és pontos szabványos írásos forma. Az eredményt közvetlenül egy tiszta másolatba másolhatja, és elküldheti a tanárnak. Helyes lenne először gyűrűkben meghatározni a kérdéses függvény analitikusságát, majd egyértelműen kijelenteni, hogy Laurent sorozatban minden ilyen gyűrűben bővíthető. Fontos, hogy ne veszítsük szem elől a Laurent-sorozat negatív erőket tartalmazó kifejezéseit. Koncentrálj erre, amennyire csak lehetséges. Használja ki jól Laurent tételét egy függvény egész hatványokban való kiterjesztésére. A funkcionális sorozatok elméletében a központi helyet a függvény sorozattá bővítésének szentelt rész foglalja el. Így a feladat be van állítva: adott függvényre
olyan hatványsort kell találnunk amely egy bizonyos intervallumon konvergált és összege egyenlő volt Ezt a feladatot az ún egy függvény hatványsorrá bővítésének problémája. Egy hatványsorbeli függvény felbonthatóságának szükséges feltétele végtelen számú differenciálhatósága - ez következik a konvergens hatványsorok tulajdonságaiból. Ez a feltétel rendszerint teljesül az elemi függvények definíciós tartományában. Tehát tegyük fel, hogy a függvény Tegyük fel, hogy a függvény Ahol A 0 ,A 1 ,A 2 ,...,A P ,...
– ismeretlen (még) együtthatók. Tegyük egyenlőségbe (*) az értéket x = x 0 ,
akkor kapunk Differenciáljuk tagonként a hatványsort (*). és hinni itt x = x 0 ,
kapunk A következő differenciálással megkapjuk a sorozatot hinni x = x 0 ,
kapunk Után P-többszörös megkülönböztetést kapunk Feltételezve az utolsó egyenlőségben x = x 0 ,
kapunk Tehát az együtthatók megtalálhatók melyiket behelyettesítve a sorozatba (*), azt kapjuk Az így kapott sorozatot ún Taylor mellett
funkcióhoz
Így ezt megállapítottuk ha a függvény hatványsorrá bővíthető (x - x 0 ), akkor ez a bővítés egyedi, és az így kapott sorozat szükségszerűen egy Taylor-sorozat. Megjegyzendő, hogy a Taylor-sor bármely függvényre megkapható, amelynek a pontban tetszőleges sorrendű deriváltjai vannak x = x 0 .
De ez nem jelenti azt, hogy a függvény és a kapott sorozat közé egyenlőségjelet lehet tenni, pl. hogy a sorozat összege egyenlő az eredeti függvénnyel. Egyrészt egy ilyen egyenlőségnek csak a konvergencia tartományában lehet értelme, és a függvényre kapott Taylor-sor eltérhet, másrészt ha a Taylor-sor konvergál, akkor összege nem feltétlenül esik egybe az eredeti függvénnyel. Fogalmazzunk meg egy állítást, amelynek segítségével a feladat megoldódik. Ha a funkció
AholR n (x)-a Taylor-formula fennmaradó tagja – a formája (Lagrange forma) Ahol
pontξ
x és x között van 0 . Vegyük észre, hogy van különbség a Taylor-sorozat és a Taylor-formula között: a Taylor-formula véges összeg, azaz. P - fix szám. Emlékezzünk vissza, hogy a sorozat összege S(x)
részösszegek funkcionális sorozatának határaként definiálható S P (x)
bizonyos időközönként x: Eszerint egy függvényt Taylor-sorozattá bővíteni azt jelenti, hogy olyan sorozatot kell találni, amely bármelyikhez xx Írjuk fel a Taylor-képletet hol alakban vegye észre, az Ha Így bebizonyítottuk egy Taylor-sor függvényének felbonthatóságának kritériuma.
A funkció érdekébenf(x) Taylor sorozattá bővül, szükséges és elegendő, hogy ezen az intervallumon
A megfogalmazott kritériumot felhasználva megkapható elegendőegy függvény felbonthatóságának feltételei egy Taylor sorozatban.
Ha beaz x pont valamelyik környéke 0 a függvény összes deriváltjának abszolút értéke ugyanarra az M számra korlátozódik≥ 0, azaz A fentiekből az következik algoritmusfunkcióbővítés
f(x) a Taylor sorozatban pont közelében x 0 :
1.
Függvények deriváltjainak keresése f(x):
f(x), f’(x), f”(x), f’”(x), f (n) (x),… 2. Számítsa ki a függvény értékét és deriváltjainak értékét a pontban! x 0 f(x 0
), f’(x 0
), f”(x 0
), f’”(x 0
), f (n) (x 0
),…
3. Formálisan felírjuk a Taylor-sort, és megtaláljuk a kapott hatványsorok konvergenciatartományát. 4. Ellenőrizzük az elegendő feltétel teljesülését, pl. melyre megállapítjuk x a konvergencia régióból, hátralévő táv R n (x)
nullára hajlamos, mint A függvények Taylor-sorozattá történő kiterjesztését ezzel az algoritmussal ún függvény definíció szerint Taylor-sorozattá történő kiterjesztése vagy közvetlen bomlás. A funkcionális sorozatok közül a legfontosabb helyet a teljesítménysorok foglalják el. A hatványsorozat egy sorozat amelyeknek a feltételei növekvő nemnegatív egész hatványokba rendezett hatványfüggvények x, A c0
, c 1
, c 2
, c n
- állandó értékek. Számok c1
, c 2
, c n
- a sorozattagok együtthatói, c0
- ingyenes tag. A hatványsorok feltételei a teljes számegyenesen vannak definiálva. Ismerkedjünk meg a fogalommal hatványsorok konvergenciájának területei.
Ez változó értékek halmaza x, amelyre a sorozat konvergál. A hatványsorok meglehetősen egyszerű konvergenciarégióval rendelkeznek. Valós változó értékekhez x a konvergencia régió vagy egy pontból áll, vagy egy bizonyos intervallum (konvergencia intervallum), vagy egybeesik a teljes tengellyel Ökör
. Az értékek hatványsorba való behelyettesítésekor x= 0 számsort eredményez c0
+0+0+...+0+...
, ami összefolyik. Ezért mikor x= 0 bármely hatványsor konvergál, és ezért konvergencia területe
nem lehet az üres halmaz. Az összes hatványsor konvergenciatartományának szerkezete azonos. Megállapítható a következő tétel segítségével. 1. tétel (Ábel tétel). Ha egy hatványsor valamilyen értéknél konvergál x = x 0
, nullától eltérő, akkor konvergál, és ráadásul abszolút, minden értékre |x| < |x 0
|
. Figyelem: mind az „X nulla” kezdőérték, mind az „X” bármely, a kezdőértékkel összehasonlított értéke modulo - az előjel figyelembevétele nélkül. Következmény. Ha teljesítménysorok eltérnek
valamilyen értéken x = x 1
, akkor minden értéknél eltér |x| > |x 1
|
. Amint azt már korábban megtudtuk, bármely hatványsor az értéken konvergál x= 0. Vannak hatványsorok, amelyek csak akkor konvergálnak x= 0, és más értékek esetén eltérés x. Ha ezt az esetet figyelmen kívül hagyjuk, feltételezzük, hogy a hatványsor valamilyen értéknél konvergál x = x 0
, nullától eltérő. Ekkor Ábel tétele szerint a ]-| intervallum minden pontjában konvergál x0
|, |x 0
|[
(olyan intervallum, amelynek bal és jobb oldali határa az az x érték, amelynél a hatványsorok konvergálnak, mínusz és plusz előjellel felvéve), szimmetrikus az origóhoz képest. Ha a hatványsor egy bizonyos értéknél eltér x = x 1
, akkor az Ábel-tétel következménye alapján a szakaszon kívül minden pontban eltér [-| x1
|, |x 1
|]
. Ebből következik, hogy bármely hatványsorhoz létezik az origóra szimmetrikus intervallum, ún konvergencia intervallum
, amelynek minden pontjában a sorozat konvergál, a határokon konvergálhat, vagy eltérhet, és nem feltétlenül egyszerre, és a szegmensen kívül a sorozat eltér. Szám R hatványsorok konvergencia sugarának nevezzük. Különleges esetekben hatványsorok konvergencia intervalluma
pontig degenerálódhat (akkor a sorozat csak akkor konvergál, ha x= 0, és annak tekinthető R= 0) vagy a teljes számegyenest ábrázolja (ekkor a sorozat a számegyenes minden pontjában konvergál, és feltételezzük, hogy ). Így egy hatványsor konvergenciatartományának meghatározása annak meghatározásából áll konvergencia sugár
Rés a sorozatok konvergenciájának tanulmányozása a konvergencia intervallum határain (at). 2. tétel. Ha egy hatványsor összes együtthatója egy bizonyostól kezdődően különbözik nullától, akkor a konvergencia sugara megegyezik a sorozat közös következő tagjainak együtthatói abszolút értékeinek arányával. , azaz 1. példa. Határozzuk meg a hatványsorok konvergenciatartományát Megoldás. Itt A (28) képlet segítségével megtaláljuk ennek a sorozatnak a konvergencia sugarát: Vizsgáljuk meg a sorozatok konvergenciáját a konvergencia intervallum végén. A 13. példa azt mutatja, hogy ez a sorozat konvergál a x= 1 és eltér a x= -1. Következésképpen a konvergencia tartománya a félintervallum. 2. példa Határozza meg a hatványsorok konvergenciatartományát Megoldás. A sorozat együtthatói pozitívak, és Keressük ennek az aránynak a határát, azaz! a hatványsorok konvergencia sugara: Vizsgáljuk meg a sorozatok konvergenciáját az intervallum végén. Az értékek helyettesítése x= -1/5 és x= 1/5 ebben a sorban a következőket adja: E sorozatok közül az első konvergál (lásd az 5. példát). Ekkor azonban az „Abszolút konvergencia” szakasz tétele értelmében a második sorozat is konvergál, és konvergenciájának tartománya a szegmens 3. példa Határozza meg a hatványsorok konvergencia tartományát Megoldás. Itt A (28) képlet segítségével megtaláljuk a sorozat konvergencia sugarát: Vizsgáljuk meg a sorozatok konvergenciáját az értékekhez. Ha behelyettesítjük őket ebben a sorozatban, akkor rendre megkapjuk Mindkét sorozat eltér, mert a konvergencia szükséges feltétele nem teljesül (közös feltételeik nem szoktak nullázni a -nál). Tehát a konvergencia intervallum mindkét végén ez a sorozat divergál, és a konvergencia tartománya az intervallum. 5. példa Határozza meg a hatványsorok konvergenciatartományát! Megoldás. Megtaláljuk az összefüggést ahol , és A (28) képlet szerint ennek a sorozatnak a konvergencia sugara vagyis a sorozat csak akkor konvergál x= 0, és más értékeknél eltér x. A példák azt mutatják, hogy a konvergencia intervallum végén a sorozatok eltérően viselkednek. Az 1. példában a konvergencia intervallum egyik végén a sorozat konvergál, a másikon pedig divergál, a 2. példában mindkét végén konvergál, a 3. példában pedig mindkét végén divergál. A hatványsorok konvergencia sugarának képletét azzal a feltételezéssel kapjuk meg, hogy a sorozattagok összes együtthatója egy bizonyos ponttól kezdve nullától eltérő. Ezért a (28) képlet használata csak ezekben az esetekben megengedett. Ha ez a feltétel megsérül, akkor a hatványsorok konvergencia sugarát kell keresni d'Alembert jele, vagy a változó lecserélésével a sorozatot olyan alakra alakítjuk, amelyben a megadott feltétel teljesül. 6. példa Határozza meg a hatványsorok konvergencia intervallumát Megoldás. Ez a sorozat nem tartalmaz páratlan fokozatú kifejezéseket x. Ezért átalakítjuk a sorozatot, beállítást. Aztán megkapjuk a sorozatot hogy megtaláljuk a konvergencia sugarát, amelyhez alkalmazhatjuk a (28) képletet. Mivel , a , akkor ennek a sorozatnak a konvergencia sugara A kapott egyenlőségből tehát ez a sorozat az intervallumhoz konvergál. Hagyjuk a hatványsorokat konvergencia sugár R> 0, azaz ez a sorozat az intervallumhoz konvergál. Ezután minden érték x a konvergencia intervallumból a sorozat egy bizonyos összegének felel meg. Ezért a hatványsorok összege függvénye x a konvergencia intervallumon. Azzal jelölve f(x), felírhatjuk az egyenlőséget megértése abban az értelemben, hogy a sorozat összege az egyes pontokban x a konvergencia intervallumból egyenlő a függvény értékével f(x) ezen a ponton. Ugyanebben az értelemben azt mondjuk, hogy a (29) hatványsor a függvényhez konvergál f(x) a konvergencia intervallumon. A konvergencia intervallumon kívül a (30) egyenlőségnek nincs értelme. 7. példa. Keresse meg a hatványsorok összegét! Megoldás. Ez egy geometriai sorozat, amelyhez a= 1, a q= x. Ezért az összege függvény csak értékekre érvényes, bár a függvény Bizonyítható, hogy a hatványsor összege f(x) folyamatos és differenciálható a konvergenciaintervallum bármely intervallumán, különösen a sorozat konvergenciaintervallumának bármely pontján. Mutassunk be tételeket a hatványsorok tagonkénti differenciálására és integrálására. 1. tétel. A (30) hatványsor a konvergenciájának intervallumában korlátlan számú tagonként differenciálható, és az így kapott hatványsorok az eredeti sorozattal megegyező konvergenciasugarakkal rendelkeznek, összegük rendre egyenlő. 2. tétel. Hatványsorok (30) 0-tól tagig korlátlan számú alkalommal integrálhatók tagonként x, ha , és az eredményül kapott hatványsorok konvergenciasugara megegyezik az eredeti sorozatéval, és összegük ennek megfelelően egyenlő Legyen adott a függvény f(x), amelyet hatványsorrá kell bővíteni, azaz. ábrázolja a (30) formában: A feladat az együtthatók meghatározása ……………………………………………….. (31) Feltételezve a (30) és (31) egyenlőségeket x= 0, azt találjuk A talált kifejezéseket a (30) egyenlőségbe behelyettesítve megkapjuk Nézzük meg néhány elemi függvény Maclaurin-soros kiterjesztését. 8. példa. Bontsa ki a függvényt egy Maclaurin sorozatban Megoldás. Ennek a függvénynek a deriváltjai egybeesnek magával a függvénnyel: Ezért mikor x= 0 van nálunk Ha ezeket az értékeket behelyettesítjük a (32) képletbe, megkapjuk a kívánt kiterjesztést: Ez a sorozat a teljes számegyenesen (a konvergencia sugarán) konvergál.
Megoldás. Az (1) bővítésben az x-et -x 2-re cseréljük, így kapjuk:
, -∞
Megoldás. Nekünk van
A (4) képlet segítségével felírhatjuk:
a képletben x helyett –x-et behelyettesítve a következőt kapjuk:
Innen a következőt kapjuk: ln(1+x)-ln(1-x) = -
A zárójeleket kinyitva, a sorozat feltételeit átrendezve és hasonló kifejezéseket hozva azt kapjuk
. Ez a sorozat a (-1;1) intervallumban konvergál, mivel két sorozatból származik, amelyek mindegyike ebben az intervallumban konvergál.
Az (1)-(5) képletekkel a megfelelő függvények Taylor sorozattá is bővíthetők, pl. függvények bővítéséhez pozitív egész hatványokban ( Ha). Ehhez egy adott függvényen olyan azonos transzformációkat kell végrehajtani, hogy megkapjuk az (1)-(5) függvények valamelyikét, amelyben helyette x k( Ha) m , ahol k konstans szám, m pozitív egész szám. Gyakran kényelmes a változó megváltoztatása t=Haés a kapott függvényt kibővítjük a Maclaurin-sor t függvényében.
Megoldás. Először megtaláljuk az 1-x-6x 2 =(1-3x)(1+2x) , .
elemihez:
konvergenciarégióval |x|< 1/3.
Megoldás. Ez a probléma a korábbiakhoz hasonlóan megoldható a Taylor sorozat definíciójával, amelyhez meg kell találnunk a függvény deriváltjait és azok értékeit x=3. A meglévő bővítmény (5) használata azonban egyszerűbb lesz:
=
Az így kapott sorozat –3-nál konvergál
Megoldás.
A sorozat , vagy -2 értéknél konvergál< x < 5.
Megoldás. Tegyük a t=x-2 cserét:
A (3) kiterjesztéssel, amelyben x helyére π / 4 t-t cserélünk, kapjuk:
Az eredményül kapott sorozat -∞-nél konvergál az adott függvényhez< π / 4 t<+∞, т.е. при (-∞
, (-∞Hozzávetőleges számítások hatványsorok használatával
A teljesítménysorokat széles körben használják közelítő számításokban. Segítségükkel adott pontossággal kiszámíthatja a gyökök, a trigonometrikus függvények, a számok logaritmusainak és a határozott integrálok értékeit. A sorozatokat differenciálegyenletek integrálásakor is használják.
Tekintsük egy függvény kiterjesztését egy hatványsorban:
Egy függvény közelítő értékének kiszámításához egy adott pontban x, amely a jelzett sorozatok konvergencia tartományába tartozik, az elsők maradnak a kiterjesztésében n tagok ( n– véges szám), és a többi kifejezést el kell vetni:
A kapott közelítő érték hibájának becsléséhez meg kell becsülni az rn (x) eldobott maradékot. Ehhez használja a következő technikákat:
Megoldás. Használjuk azt a bővítést, ahol x=1/2 (lásd az 5. példát az előző témakörben):
Vizsgáljuk meg, hogy a bővítés első három tagja után el tudjuk-e vetni a maradékot, ehhez egy végtelenül csökkenő geometriai progresszió összegével értékeljük ki:
Tehát ezt a maradékot eldobhatjuk, és megkapjuk
Megoldás. Használjuk a binomiális sorozatot. Mivel az 5 3 a 130-hoz legközelebb eső egész szám kocka, célszerű a 130-at úgy ábrázolni, hogy 130 = 5 3 +5. 
mivel a kapott váltakozó sorozatnak már a Leibniz-kritériumot kielégítő negyedik tagja is kisebb, mint a szükséges pontosság:
, így az és az azt követő kifejezések elvethetők.
A Newton-Leibniz formulával sok gyakorlatilag szükséges határozott vagy nem megfelelő integrál nem számítható ki, mert alkalmazása az antiderivált megtalálásához kapcsolódik, aminek gyakran nincs kifejezése elemi függvényekben. Az is előfordul, hogy lehetséges az antiderivatív megtalálása, de ez feleslegesen munkaigényes. Ha azonban az integrandusfüggvényt hatványsorrá bővítjük, és az integrálás határai ennek a sorozatnak a konvergencia intervallumához tartoznak, akkor lehetséges az integrál közelítő kiszámítása előre meghatározott pontossággal.
Megoldás. A megfelelő határozatlan integrál nem fejezhető ki elemi függvényekkel, azaz. „nem állandó integrált” jelent. A Newton-Leibniz képlet itt nem alkalmazható. Számítsuk ki közelítőleg az integrált.
A bűn sorozatának tagokra osztása x tovább x, kapunk: 
Ezt a sorozatot tagonként integrálva (ez azért lehetséges, mert az integráció határai ennek a sorozatnak a konvergencia intervallumához tartoznak), kapjuk:
Mivel a kapott sorozat kielégíti Leibniz feltételeit, és elegendő az első két tag összegét felvenni, hogy adott pontossággal megkapjuk a kívánt értéket.
Így azt találjuk  .
.
Megoldás.

![]() . Vizsgáljuk meg, hogy a kapott sorozat második tagja után el tudjuk-e dobni a maradékot.
. Vizsgáljuk meg, hogy a kapott sorozat második tagja után el tudjuk-e dobni a maradékot.
0,0001<0.001. Следовательно,  .
. ,
azok.
,
azok. =
..
=
..
 bármilyen rendű származékai vannak. Lehetséges-e hatványsorozattá bővíteni?Ha igen, hogyan találjuk meg ezt a sorozatot? A probléma második része könnyebben megoldható, ezért kezdjük vele.
bármilyen rendű származékai vannak. Lehetséges-e hatványsorozattá bővíteni?Ha igen, hogyan találjuk meg ezt a sorozatot? A probléma második része könnyebben megoldható, ezért kezdjük vele. a pontot tartalmazó intervallumban konvergáló hatványsor összegeként ábrázolható x 0 :
a pontot tartalmazó intervallumban konvergáló hatványsor összegeként ábrázolható x 0 :
 =
..
(*)
=
..
(*) .
. =
..
=
..
 .
. =
..
=
..
 , ahol
, ahol  .
. , ahol
, ahol
 ,
,
 ,
,
 ,
…,
,
…,
 ,….,
,…., .
.
3.2. Elegendő feltételek egy függvény felbonthatóságához egy Taylor sorozatban
 az x pont valamelyik szomszédságában 0 legfeljebb (n+
1) sorrendben, akkor ezen a környéken vanképlet
Taylor
az x pont valamelyik szomszédságában 0 legfeljebb (n+
1) sorrendben, akkor ezen a környéken vanképlet
Taylor

 .
.
 meghatározza a kapott hibát, cserélje ki a függvényt f(x)
polinom S n (x).
meghatározza a kapott hibát, cserélje ki a függvényt f(x)
polinom S n (x).
 , Azt
, Azt  ,azok. a funkció Taylor sorozattá bővül. Fordítva, ha
,azok. a funkció Taylor sorozattá bővül. Fordítva, ha  , Azt
, Azt  .
. , AholR n (x) a Taylor sorozat többi tagja.
, AholR n (x) a Taylor sorozat többi tagja. , To ezen a környéken a függvény Taylor sorozattá bővül.
, To ezen a környéken a függvény Taylor sorozattá bővül. vagy
vagy
 .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]() :
:![]()
![]() ,
,![]()
![]()
![]()
Hatványsorok összege. Hatványsorok differenciálása és integrálása
![]()
![]() . Egy sorozat akkor konvergál, ha , és a konvergencia intervallum. Ezért egyenlőség
. Egy sorozat akkor konvergál, ha , és a konvergencia intervallum. Ezért egyenlőség![]()
![]() minden értékre meghatározva x, kivéve x= 1.
minden értékre meghatározva x, kivéve x= 1.
A függvények hatványsorokká bővítése
![]() sor (30). Ennek érdekében az egyenlőséget (30) tagonként megkülönböztetve következetesen azt tapasztaljuk, hogy:
sor (30). Ennek érdekében az egyenlőséget (30) tagonként megkülönböztetve következetesen azt tapasztaljuk, hogy:![]()
![]()
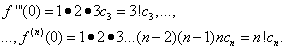
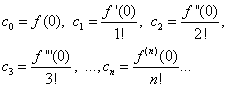
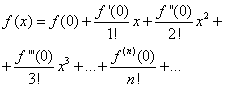 (32)
(32)
![]() (33)
(33)

