prirodna vrijednost. Prirodni brojevi – osnove

Brojevi su apstraktan pojam. Oni su kvantitativna karakteristika objekata i bivaju realni, racionalni, negativni, cijeli i frakcijski, kao i prirodni.

U brojanju se obično koristi prirodni niz, u kojem prirodno proizlaze oznake količine. Upoznavanje s računom počinje u ranom djetinjstvu. Koje je dijete izbjegavalo smiješne brojalice u kojima su samo korišteni elementi prirodne brojalice? "Jedan, dva, tri, četiri, pet ... Zeko je izašao u šetnju!" ili "1, 2, 3, 4, 5, 6, 7, 8, 9, 10, kralj je odlučio da me objesi..."

Za svaki prirodni broj možete pronaći drugi, veći od njega. Taj se skup obično označava slovom N i treba ga smatrati beskonačnim u smjeru povećanja. Ali ovaj skup ima početak - ovo je jedinica. Iako postoje francuski prirodni brojevi, čiji skup također uključuje nulu. Ali glavne značajke razlikovanja oba skupa je činjenica da ne uključuju ni razlomke ni negativne brojeve.

Potreba za brojanjem raznih predmeta pojavila se u prapovijesti. Tada je navodno formiran koncept "prirodnih brojeva". Njegovo formiranje odvijalo se kroz cijeli proces promjene svjetonazora osobe, razvoja znanosti i tehnologije.

Međutim, još nisu mogli apstraktno razmišljati. Bilo im je teško razumjeti što je zajedničko pojmovima "tri lovca" ili "tri stabla". Dakle, kod označavanja broja ljudi korištena je jedna definicija, a kod označavanja istog broja predmeta različite vrste korištena je sasvim druga definicija.

I bilo je izuzetno kratko. U njemu su bili prisutni samo brojevi 1 i 2, a brojanje je završavalo konceptom "mnogo", "stado", "gomila", "hrpa".

Kasnije je formiran progresivniji račun, već širi. Zanimljiva je činjenica da su postojala samo dva broja - 1 i 2, a sljedeći su brojevi već dobiveni zbrajanjem.

Primjer za to su podaci koji su došli do nas o nizu brojeva australskog plemena. Oni su 1 označavali riječ "Enza", a 2 - riječ "petcheval". Broj 3 je stoga zvučao kao "petcheval-Enza", a 4 - već kao "petcheval-petcheval".

Većina naroda prepoznala je prste kao standard za brojanje. Nadalje, razvoj apstraktnog koncepta "prirodnih brojeva" išao je putem korištenja zareza na štapiću. A onda je došlo do potrebe da se desetak označi drugim znakom. Stari ljudi, naš izlaz, počeli su koristiti drugi štap, na kojem su napravljeni zarezi, označavajući desetice.

Mogućnosti reprodukcije brojeva iznimno su se proširile s pojavom pisma. Prvo su se brojevi prikazivali kao crtice na glinenim pločicama ili papirusu, ali su se postupno za pisanje počeli koristiti i drugi znakovi.Tako su se pojavili rimski brojevi.

Mnogo kasnije se pojavio koji je otvorio mogućnost pisanja brojeva s relativno malim skupom znakova. Danas nije teško zapisati tako ogromne brojke kao što su udaljenost između planeta i broj zvijezda. Treba samo naučiti kako koristiti stupnjeve.

Euklid u 3. stoljeću prije Krista u knjizi „Počeci" utvrđuje beskonačnost numeričkog skupa. A Arhimed u „Psamitu" otkriva principe za konstruiranje imena proizvoljno velikih brojeva. Gotovo do sredine 19. stoljeća ljudi se nisu suočili s potrebom za jasnom formulacijom pojma "prirodnih brojeva". Definicija je bila potrebna s pojavom aksiomatske matematičke metode.

A 70-ih godina 19. stoljeća formulirao je jasnu definiciju prirodnih brojeva temeljenu na konceptu skupa. A danas već znamo da su svi prirodni brojevi cijeli brojevi, u rasponu od 1 do beskonačnosti. Mala djeca, čineći prvi korak u upoznavanju kraljice svih znanosti - matematike - počinju proučavati ove brojeve.

1.1 Definicija

Nazivaju se brojevi koje ljudi koriste kada broje prirodni(npr. jedan, dva, tri, ..., sto, sto jedan, ..., tri tisuće dvjesto dvadeset i jedan, ...) Za pisanje prirodnih brojeva koriste se posebni znakovi (simboli) , nazvao figure.

Danas prihvaćeno decimalni zapis. Dekadni sustav (ili način) zapisivanja brojeva koristi arapske brojeve. Ovo je deset različitih znamenki: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 .

Najmanje prirodni broj je broj jedan, to napisano decimalnom znamenkom - 1. Sljedeći prirodni broj dobiva se od prethodnog (osim jednog) dodavanjem 1 (jedan). Ovo zbrajanje se može učiniti mnogo puta (beskonačno mnogo puta). To znači da Ne najveći prirodni broj. Stoga se kaže da je niz prirodnih brojeva neograničen ili beskonačan, budući da nema kraja. Prirodni brojevi se pišu decimalnim znamenkama.

1.2. Broj "nula"

Da biste označili odsutnost nečega, upotrijebite broj " nula" ili " nula". Zapisuje se brojevima. 0 (nula). Na primjer, u kutiji su sve kuglice crvene. Koliko ih je zelenih? - Odgovor: nula . Dakle, u kutiji nema zelenih kuglica! Broj 0 može značiti da je nešto gotovo. Na primjer, Masha je imala 3 jabuke. Dvije je podijelila prijateljima, jednu je sama pojela. Dakle, otišla je 0 (nula) jabuka, tj. nijedan nije ostao. Broj 0 može značiti da se nešto nije dogodilo. Na primjer, hokejaška utakmica između ruske i kanadske momčadi završila je rezultatom 3:0 (čitaj "tri - nula") u korist ruskog tima. To znači da je ruski tim postigao 3 gola, a kanadski tim 0 golova, a nisu mogli postići niti jedan gol. Moramo zapamtiti da nula nije prirodan broj.

1.3. Zapisivanje prirodnih brojeva

U decimalnom načinu zapisivanja prirodnog broja svaka znamenka može označavati različite brojeve. Ovisi o mjestu ove znamenke u zapisu broja. Određeno mjesto u zapisu prirodnog broja naziva se položaj. Stoga se decimalni zapis naziva pozicijski. Razmotrimo decimalni zapis 7777 broja sedam tisuća sedamsto sedamdeset sedam. U ovom unosu ima sedam tisuća, sedam stotina, sedam desetica i sedam jedinica.

Svako od mjesta (položaja) u decimalnom zapisu broja naziva se pražnjenje. Svake tri znamenke kombiniraju se u Klasa. Ovo spajanje se izvodi s desna na lijevo (od kraja unosa broja). Različiti činovi i klase imaju svoja imena. Broj prirodnih brojeva je neograničen. Stoga broj činova i klasa također nije ograničen ( beskrajno). Razmotrite nazive znamenki i klasa na primjeru broja s decimalnim zapisom

38 001 102 987 000 128 425:

Klase i činovi
kvintilijuni		stotine kvintilijuna
		deseci kvintilijuna
		kvintilijuni
kvadrilijuni		stotine kvadrilijuna
		deseci kvadrilijuna
		kvadrilijuni
bilijuni		stotine bilijuna
		deseci trilijuna
		bilijuni
milijarde		stotine milijardi
		deseci milijardi
		milijarde
milijuni		stotine milijuna
		desetke milijuna
		milijuni
		stotine tisuća
		desetke tisuća

Dakle, klase, počevši od najmlađih, imaju nazive: jedinice, tisuće, milijuni, milijarde, bilijuni, kvadrilijuni, kvintilijuni.

1.4. Bitne jedinice

Svaka od klasa u zapisu prirodnih brojeva sastoji se od tri znamenke. Svaki rang ima bitne jedinice. Sljedeći brojevi nazivaju se bit jedinice:

1 - znamenka jedinica znamenke jedinica,

10 - znamenkasta jedinica znamenke desetica,

100 - bitna jedinica znamenke stotine,

1 000 - bitna jedinica tisućitnog mjesta,

10 000 - znamenkasta jedinica desetaka tisuća,

100 000 - bitna jedinica stotina tisuća,

1.000.000 je znamenkasta jedinica znamenke milijuna itd.

Broj u bilo kojoj od znamenki pokazuje broj jedinica te znamenke. Dakle, broj 9, na mjestu stotina milijardi, znači da broj 38.001.102.987.000 128.425 uključuje devet milijardi (to jest, 9 puta 1.000.000.000 ili 9 bitnih jedinica milijardi). Prazna znamenka stotina kvintilijuna znači da u ovom broju nema stotina kvintilijuna ili je njihov broj jednak nuli. U ovom slučaju broj 38 001 102 987 000 128 425 može se napisati na sljedeći način: 038 001 102 987 000 128 425.

Možete ga napisati i drugačije: 000 038 001 102 987 000 128 425. Nule na početku broja označavaju prazne znamenke višeg reda. Obično se ne pišu, za razliku od nula unutar decimalnog zapisa, koje nužno označavaju prazne znamenke. Dakle, tri nule u klasi milijuna znače da su znamenke stotina milijuna, desetaka milijuna i jedinica milijuna prazne.

1.5. Kratice u pisanju brojeva

Pri pisanju prirodnih brojeva koriste se kratice. Evo nekoliko primjera:

1.000 = 1 tisuća (tisuću)

23.000.000 = 23 milijuna (dvadeset tri milijuna)

5.000.000.000 = 5 milijardi (pet milijardi)

203 000 000 000 000 = 203 bilijuna (dvjesto tri bilijuna)

107 000 000 000 000 000 = 107 sqd. (sto sedam kvadrilijuna)

1.000.000.000.000.000.000 = 1 kw. (jedan kvintilijun)

Blok 1.1. Rječnik

Sastavite rječnik novih pojmova i definicija iz §1. Da biste to učinili, u prazne ćelije unesite riječi s donjeg popisa pojmova. U tablici (na kraju bloka) za svaku definiciju označite broj pojma s popisa.

Blok 1.2. Samostalni trening

U svijetu velikih brojeva

Ekonomija .

1. Proračun Rusije za sljedeću godinu bit će: 6328251684128 rubalja.
2. Planirani troškovi za ovu godinu: 5124983252134 rubalja.
3. Prihodi zemlje premašili su rashode za 1203268431094 rubalja.

Pitanja i zadaci

1. Pročitaj sva tri navedena broja
2. Napiši znamenke u milijunskoj klasi svakog od tri broja

1. Kojem dijelu u svakom od brojeva pripada znamenka na sedmom mjestu od kraja zapisa brojeva?
2. Koliki broj bitnih jedinica pokazuje broj 2 u prvom broju?... u drugom i trećem broju?
3. Imenuj bitnu jedinicu za osmo mjesto od kraja u zapisu triju brojeva.

Geografija (duljina)

1. Ekvatorijalni polumjer Zemlje: 6378245 m
2. Opseg ekvatora: 40075696 m
3. Najveća dubina svjetskog oceana (Marijanska brazda u Tihom oceanu) 11500 m

Pitanja i zadaci

1. Pretvorite sve tri vrijednosti u centimetre i pročitajte dobivene brojeve.
2. Za prvi broj (u cm) upišite brojeve u odjeljke:

stotine tisuća _______

deseci milijuna _______

tisuće _______

milijarde _______

stotine milijuna _______

1. Za drugi broj (u cm) zapišite bitne jedinice koje odgovaraju brojevima 4, 7, 5, 9 u unosu broja

1. Pretvorite treću vrijednost u milimetre, pročitajte dobiveni broj.
2. Za sva mjesta u zapisu trećeg broja (u mm) označite znamenke i znamenke u tablici:

Geografija (kvadrat)

1. Površina cijele površine Zemlje je 510.083 tisuća četvornih kilometara.
2. Površina suma na Zemlji iznosi 148.628 tisuća četvornih kilometara.
3. Površina Zemljine vodene površine iznosi 361.455 tisuća četvornih kilometara.

Pitanja i zadaci

1. Pretvorite sve tri vrijednosti u kvadratne metre i pročitajte dobivene brojeve.
2. Imenujte klase i rangove koji odgovaraju znamenkama različitim od nule u zapisu ovih brojeva (u kvadratnim m).
3. U unosu trećeg broja (u kv. M) navedite bitne jedinice koje odgovaraju brojevima 1, 3, 4, 6.
4. U dva unosa druge vrijednosti (u četvornim kilometrima i četvornim metrima) označite kojoj znamenki pripada broj 2.
5. Zapišite bitne jedinice za broj 2 u zapisima druge vrijednosti.

Blok 1.3. Dijalog s računalom.

Poznato je da se veliki brojevi često koriste u astronomiji. Navedimo primjere. Prosječna udaljenost Mjeseca od Zemlje je 384 tisuće km. Udaljenost Zemlje od Sunca (prosječno) je 149 504 tisuća km, Zemlje od Marsa je 55 milijuna km. Na računalu pomoću uređivača teksta Word izradite tablice tako da svaka znamenka u zapisu navedenih brojeva bude u zasebnoj ćeliji (ćeliji). Da biste to učinili, izvršite naredbe na alatnoj traci: tablica → dodaj tablicu → broj redaka (kursorom stavite “1”) → broj stupaca (izračunajte sami). Napravite tablice za ostale brojeve (blok "Samopriprema").

Blok 1.4. Štafeta velikih brojeva

Prvi redak tablice sadrži veliki broj. Čitati. Zatim dovršite zadatke: pomicanjem brojeva u unosu brojeva udesno ili ulijevo dođite do sljedećih brojeva i pročitajte ih. (Ne pomičite nule na kraju broja!). U razredu se štafeta može izvoditi međusobnom predajom.

Linija 2 . Pomaknite sve znamenke broja u prvom retku ulijevo kroz dvije ćelije. Brojeve 5 zamijenite brojem koji slijedi. Ispunite prazna polja nulama. Pročitajte broj.

Linija 3 . Pomaknite sve znamenke broja u drugom retku udesno kroz tri ćelije. Brojeve 3 i 4 u unosu brojeva zamijenite sljedećim brojevima. Ispunite prazna polja nulama. Pročitajte broj.

Linija 4. Pomaknite sve znamenke broja u retku 3 jednu ćeliju ulijevo. Broj 6 u klasi bilijuna promijenite u prethodni, a u klasi milijardi u sljedeći broj. Ispunite prazna polja nulama. Pročitajte dobiveni broj.

redak 5 . Pomaknite sve znamenke broja u retku 4 jednu ćeliju udesno. Zamijenite broj 7 na mjestu “desetak tisuća” prethodnim, a na mjestu “desetak milijuna” sljedećim. Pročitajte dobiveni broj.

redak 6 . Pomaknite sve znamenke broja u retku 5 ulijevo nakon 3 ćelije. Promijenite broj 8 na mjestu stotina milijardi na prethodni, a broj 6 na mjestu stotina milijuna na sljedeći broj. Ispunite prazna polja nulama. Izračunajte dobiveni broj.

Linija 7 . Pomaknite sve znamenke broja u retku 6 udesno za jednu ćeliju. Zamijenite znamenke u desecima kvadrilijuna i desecima milijardi mjesta. Pročitajte dobiveni broj.

redak 8 . Pomaknite sve znamenke broja u retku 7 ulijevo kroz jednu ćeliju. Zamijenite znamenke na kvintilijunu i kvadrilijunu mjesta. Ispunite prazna polja nulama. Pročitajte dobiveni broj.

redak 9 . Pomaknite sve znamenke broja u retku 8 udesno kroz tri ćelije. Zamijenite dva susjedna broja u retku brojeva iz razreda milijuni i bilijuni. Pročitajte dobiveni broj.

redak 10 . Pomaknite sve znamenke broja u retku 9 jednu ćeliju udesno. Pročitajte dobiveni broj. Označite brojeve koji označavaju godinu održavanja Moskovske olimpijade.

Blok 1.5. Igrajmo se

Zapaliti vatru

Polje za igru ​​je slika božićnog drvca. Ima 24 žarulje. No samo ih je 12 spojeno na električnu mrežu. Za odabir spojenih svjetiljki morate točno odgovoriti na pitanja riječima "Da" ili "Ne". Istu igru ​​možete igrati i na računalu, točan odgovor “svijetli” žaruljicom.

1. Je li točno da su brojevi posebni znakovi za pisanje prirodnih brojeva? (1 - da, 2 - ne)
2. Je li točno da je 0 najmanji prirodni broj? (3 - da, 4 - ne)
3. Je li točno da u položajnom brojevnom sustavu ista znamenka može označavati različite brojeve? (5 - da, 6 - ne)
4. Je li točno da se određeno mjesto u decimalnom zapisu brojeva naziva mjestom? (7 - da, 8 - ne)
5. Zadan je broj 543 384. Je li točno da je broj najznačajnijih znamenki u njemu 543, a najnižih 384? (9 - da, 10 - ne)
6. Je li istina da je u klasi milijardi najstarija jedinica bita sto milijardi, a najmlađa jedna milijarda? (11 - da, 12 - ne)
7. Zadan je broj 458 121. Je li točno da je zbroj broja najznačajnijih znamenki i broja najmanje značajnih znamenki 5? (13 - da, 14 - ne)
8. Je li istina da je najstarija od trilijunskih jedinica klase milijun puta veća od najstarije od milijunskih jedinica? (15 - da, 16 - ne)
9. Dana su dva broja 637508 i 831. Je li istina da je najznačajniji 1 prvog broja 1000 puta najvažniji 1 drugog broja? (17 - da, 18 - ne)
10. Dan je broj 432. Je li točno da je najznačajnija bitna jedinica tog broja 2 puta veća od najmlađe? (19 - da, 20 - ne)
11. Zadan je broj 100 000 000. Je li istina da je broj bitnih jedinica koje u njemu čine 10 000 1000? (21 - da, 22 - ne)
12. Je li istina da klasi trilijuna prethodi klasa kvadrilijuna, a da klasi kvintilijuna prethodi ta klasa? (23 - da, 24 - ne)

1.6. Iz povijesti brojeva

Čovjek se od davnina suočava s potrebom da prebroji stvari, usporedi broj predmeta (npr. pet jabuka, sedam strijela...; u plemenu ima 20 muškaraca i trideset žena, ... ). Također je bilo potrebno uspostaviti red unutar određenog broja objekata. Na primjer, kada se lovi, vođa plemena ide prvi, najjači ratnik plemena dolazi drugi, i tako dalje. U te svrhe korišteni su brojevi. Za njih su izmišljena posebna imena. U govoru se nazivaju brojevima: jedan, dva, tri itd. su glavni brojevi, a prvi, drugi, treći su redni brojevi. Brojevi su se zapisivali posebnim znakovima – brojevima.

S vremenom ih je bilo brojevni sustavi. To su sustavi koji uključuju načine zapisivanja brojeva i razne radnje na njima. Najstariji poznati brojevni sustavi su egipatski, babilonski i rimski brojevni sustavi. U Rusiji su se u stara vremena za pisanje brojeva koristila slova abecede s posebnim znakom ~ (titlo). Dekadni brojevni sustav je trenutno najrašireniji. Naširoko se koriste, posebno u svijetu računala, binarni, oktalni i heksadecimalni brojevni sustavi.

Dakle, da biste napisali isti broj, možete koristiti različite znakove - brojeve. Dakle, broj četiri stotine dvadeset pet može se napisati egipatskim brojevima - hijeroglifima:

Ovo je egipatski način pisanja brojeva. Isti broj rimskim brojevima: CDXXV(rimski način pisanja brojeva) ili decimalne znamenke 425 (decimalni zapis brojeva). U binarnom zapisu to izgleda ovako: 110101001 (binarni ili binarni zapis brojeva), au oktalnom - 651 (oktalni zapis brojeva). U heksadecimalnom zapisu bit će zapisano: 1A9(heksadecimalni zapis). Možete to učiniti sasvim jednostavno: napravite, kao Robinson Crusoe, četiri stotine dvadeset i pet zareza (ili poteza) na drvenom stupu - IIIIIIIII…... III. Ovo su prve slike prirodnih brojeva.

Dakle, u decimalnom sustavu pisanja brojeva (u decimalnom načinu zapisivanja brojeva) koriste se arapske brojke. Ovo je deset različitih znakova - brojeva: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 . U binarnom obliku, dvije binarne znamenke: 0, 1; u oktalnom - osam oktalnih znamenki: 0, 1, 2, 3, 4, 5, 6, 7; u heksadecimalnom obliku - šesnaest različitih heksadecimalnih znamenki: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F; u seksagezimalnom (babilonskom) - šezdeset različitih znakova - brojeva itd.)

Decimalne znamenke stigle su u europske zemlje s Bliskog istoka, arapskih zemalja. Otuda naziv - arapski brojevi. Ali došli su do Arapa iz Indije, gdje su izumljeni sredinom prvog tisućljeća.

1.7. Sustav rimskih brojeva

Jedan od drevnih sustava brojeva koji se danas koristi je rimski sustav. U tablici dajemo glavne brojeve rimskog brojnog sustava i odgovarajuće brojeve decimalnog sustava.

rimski broj					C
				50 pedeset		500 pet stotina	1000 tisuća

Rimski brojčani sustav je sustav dodavanja. U njemu, za razliku od pozicijskih sustava (na primjer, decimalnog), svaka znamenka označava isti broj. Da, snimaj II- označava broj dva (1 + 1 = 2), zapis III- broj tri (1 + 1 + 1 = 3), zapis XXX- broj trideset (10 + 10 + 10 = 30) itd. Za pisanje brojeva vrijede sljedeća pravila.

1. Ako je manji broj nakon veći, onda se dodaje većem: VII- broj sedam (5 + 2 = 5 + 1 + 1 = 7), XVII- broj sedamnaest (10 + 7 = 10 + 5 + 1 + 1 = 17), MCL- broj tisuću sto pedeset (1000 + 100 + 50 = 1150).
2. Ako je manji broj prije veći, tada se oduzima od većeg: IX- broj devet (9 = 10 - 1), LM- broj devetsto pedeset (1000 - 50 = 950).

Za pisanje velikih brojeva morate koristiti (izmisliti) nove znakove - brojeve. U isto vrijeme, unosi brojeva ispadaju glomazni, vrlo je teško izvoditi izračune s rimskim brojevima. Tako godina lansiranja prvog umjetnog satelita Zemlje (1957.) u rimskom zapisu ima oblik MCMLVII .

Blok 1. 8. Bušena kartica

Čitanje prirodnih brojeva

Ovi se zadaci provjeravaju pomoću karte s kružićima. Objasnimo njegovu primjenu. Nakon što ste riješili sve zadatke i pronašli točne odgovore (označeni su slovima A, B, C itd.), stavite list prozirnog papira na karticu. Označite točne odgovore znakom “X” na njemu, kao i kombinacijom znaka “+”. Zatim položite prozirni list na stranicu tako da se oznake za poravnanje podudaraju. Ako su sve oznake "X" u sivim kružićima na ovoj stranici, zadaci su ispravno dovršeni.

1.9. Redoslijed čitanja prirodnih brojeva

Kod čitanja prirodnog broja postupite na sljedeći način.

1. Mentalno rastavite broj u trojke (razrede) s desna na lijevo, od kraja unosa broja.

1. Počevši od mlađeg razreda, s desna na lijevo (od kraja unosa broja), zapisuju nazive klasa: jedinice, tisuće, milijuni, milijarde, bilijuni, kvadrilijuni, kvintilijuni.
2. Pročitajte broj, počevši od srednje škole. U ovom slučaju poziva se broj bitnih jedinica i naziv klase.
3. Ako je znamenka nula (znamenka je prazna), tada se ne poziva. Ako su sve tri znamenke pozvane klase nule (znamenke su prazne), tada se ova klasa ne poziva.

Pročitajmo (imenuj) broj napisan u tablici (vidi § 1), prema koracima 1 - 4. Mentalno podijelimo broj 38001102987000128425 u klase s desna na lijevo: 038 001 102 987 000 128 425. Naznačimo imena klase u ovom broju, počevši od kraja njegovi unosi su: jedinice, tisuće, milijuni, milijarde, bilijuni, kvadrilijuni, kvintilijuni. Sada možete pročitati broj, počevši od starije klase. Imenujemo troznamenkaste, dvoznamenkaste i jednoznamenkaste brojeve, dodajući naziv odgovarajućeg razreda. Prazne klase nisu imenovane. Dobijamo sljedeći broj:

• 038 - trideset osam kvintilijuna
• 001 - jedan kvadrilijun
• 102 - sto dva bilijuna
• 987 - devet stotina osamdeset sedam milijardi
• 000 - ne imenovati (ne čitati)
• 128 - sto dvadeset osam tisuća
• 425 - četiristo dvadeset pet

Kao rezultat, prirodni broj 38 001 102 987 000 128 425 čita se na sljedeći način: "trideset osam kvintilijuna jedan kvadrilijun sto dva trilijuna devetsto osamdeset sedam milijardi sto dvadeset osam tisuća četiri stotine dvadeset pet."

1.9. Redoslijed zapisivanja prirodnih brojeva

Prirodni brojevi se pišu sljedećim redom.

1. Zapišite tri znamenke za svaku klasu, počevši od najviše klase do znamenke jedinica. U ovom slučaju, za viši razred brojeva, može biti dva ili jedan.
2. Ako klasa ili rang nisu navedeni, tada se u odgovarajuće znamenke upisuju nule.

Na primjer, broj dvadeset pet milijuna tristo dva zapisano u obliku: 25 000 302 (klasa tisućica nije imenovana, stoga se u svim znamenkama klase tisućica pišu nule).

1.10. Predstavljanje prirodnih brojeva kao zbroj bitnih članova

Navedimo primjer: 7 563 429 je decimalni prikaz broja sedam milijuna petsto šezdeset tri tisuće četiri stotine dvadeset devet. Ovaj broj sadrži sedam milijuna, petsto tisuća, šest desetica, tri tisuće, četiri stotine, dvije desetice i devet jedinica. Može se prikazati kao zbroj: 7 563 429 \u003d 7 000 000 + 500 000 + 60 000 + + 3 000 + 400 + 20 + 9. Takav se unos naziva prikazom prirodnog broja kao zbrojem bitnih članova.

Blok 1.11. Igrajmo se

Dungeon Treasures

Na igralištu je crtež za Kiplingovu bajku "Mowgli". Pet sanduka ima lokote. Da biste ih otvorili, morate riješiti probleme. U isto vrijeme, kada otvorite drvenu škrinju, dobivate jedan bod. Kada otvorite limenu škrinju, dobivate dva boda, bakrenu - tri boda, srebrnu - četiri, a zlatnu - pet. Pobjednik je onaj koji brže otvori sve škrinje. Ista igra se može igrati na računalu.

1. drvena škrinja

Pronađite koliko je novca (u tisućama rubalja) u ovoj škrinji. Da biste to učinili, trebate pronaći ukupan broj bitnih jedinica najmanjeg značaja klase milijuna za broj: 125308453231.

1. Limena škrinja

Pronađite koliko je novca (u tisućama rubalja) u ovoj škrinji. Da biste to učinili, u broju 12530845323 pronađite broj jedinica bita najmanje važnosti klase jedinica i broj jedinica bita najmanje važnosti klase milijun. Zatim pronađite zbroj tih brojeva i na desnoj strani pripišite broj na desetke milijuna.

1. Bakrena škrinja

Da biste pronašli novac ove škrinje (u tisućama rubalja), u broju 751305432198203 pronađite broj jedinica s najnižom znamenkom u klasi bilijuna i broj jedinica s najnižom znamenkom u klasi milijarde. Zatim pronađite zbroj tih brojeva i s desne strane dodijelite prirodne brojeve razreda jedinica tog broja po redoslijedu njihova rasporeda.

1. Srebrna škrinja

Novac ove škrinje (u milijunima rubalja) bit će prikazan zbrojem dvaju brojeva: brojem jedinica najniže znamenke razreda tisućica i prosječnih jedinica znamenki razreda milijarde za broj 481534185491502.

1. zlatna škrinja

Zadan je broj 800123456789123456789. Ako pomnožimo brojeve u najvišim znamenkama svih klasa ovog broja, dobit ćemo novac ove škrinje u milijunima rubalja.

Blok 1.12. Podudaranje

Napiši prirodne brojeve. Predstavljanje prirodnih brojeva kao zbroj bitnih članova

Za svaki zadatak u lijevom stupcu odaberite rješenje iz desnog stupca. Odgovor zapišite u obliku: 1a; 2g; 3b…

	Zapiši brojeve: pet milijuna dvadeset pet tisuća
	Zapiši brojeve: pet milijardi dvadeset pet milijuna
	Zapiši brojeve: pet trilijuna dvadeset pet
	Zapiši brojeve: sedamdeset sedam milijuna sedamdeset sedam tisuća sedamsto sedamdeset sedam
	Zapiši brojeve: sedamdeset sedam bilijuna sedamsto sedamdeset sedam tisuća sedam
	Zapiši brojeve: sedamdeset sedam milijuna sedamsto sedamdeset sedam tisuća sedam
	Zapiši brojeve: sto dvadeset tri milijarde četiri stotine pedeset šest milijuna sedamsto osamdeset devet tisuća
	Zapiši brojeve: sto dvadeset tri milijuna četiristo pedeset šest tisuća sedamsto osamdeset devet
	Zapiši brojeve: tri milijarde jedanaest
	Zapiši brojeve: tri milijarde jedanaest milijuna

opcija 2

	trideset dvije milijarde sto sedamdeset pet milijuna dvjesto devedeset osam tisuća tristo četrdeset jedan		100000000 + 1000000 + 10000 + 100 + 1
	Izrazite broj kao zbroj bitnih članova: tristo dvadeset jedan milijun četrdeset jedan		30000000000 + 2000000000 + 100000000 + 70000000 + 5000000 + 200000 + 90000 + 8000 + 300 + 40 + 1
	Izrazite broj kao zbroj bitnih članova: 321000175298341
	Izrazite broj kao zbroj bitnih članova: 101010101
	Izrazite broj kao zbroj bitnih članova: 11111		300000000 + 20000000 + 1000000 +
	5000000 + 300000 + 20000 + 1000
	Zapišite u decimalnom zapisu broj predstavljen kao zbroj bitnih članova: 5000000 + 300 + 20 + 1		30000000000000 + 2000000000000 + 1000000000000 + 100000000 + 70000000 + 5000000 + 200000 + 90000 + 8000 + 300 + 40 + 1
	Zapišite u decimalnom zapisu broj predstavljen kao zbroj bitnih članova: 10000000000 + 2000000000 + 100000 + 10 + 9
	Zapišite u decimalnom zapisu broj predstavljen kao zbroj bitnih članova: 10000000000 + 2000000000 + 100000000 + 10000000 + 9000000
	Zapišite u decimalnom zapisu broj predstavljen kao zbroj bitnih članova: 9000000000000 + 9000000000 + 9000000 + 9000 + 9		10000 + 1000 + 100 + 10 + 1

Blok 1.13. Fasetni test

Naziv testa dolazi od riječi "složeno oko insekata". Ovo je složeno oko koje se sastoji od zasebnih "očiju". Zadaci fasetnog testa sastavljeni su od zasebnih elemenata označenih brojevima. Fasetirani testovi obično sadrže velik broj zadataka. Ali u ovom testu postoje samo četiri zadatka, ali oni se sastoje od velikog broja elemenata. Ovo je učinjeno kako bismo vas naučili kako "skupljati" ispitne probleme. Ako ih možete sastaviti, onda se lako možete nositi s drugim aspektnim testovima.

Objasnimo kako se zadaci sastavljaju na primjeru trećeg zadatka. Sastoji se od ispitnih elemenata označenih brojevima: 1, 4, 7, 11, 1, 5, 7, 9, 10, 16, 17, 22, 21, 25

« Ako a» 1) uzeti brojeve iz tablice (broj); 4) 7; 7) smjestiti u kategoriju; 11) milijarda; 1) uzeti broj iz tablice; 5) 8; 7) postaviti ga u redove; 9) deseci milijuna; 10) stotine milijuna; 16) stotine tisuća; 17) deseci tisuća; 22) smjestite brojeve 9 i 6 na mjesta tisućica i stotina. 21) popunite preostale znamenke nulama; " ZATIM» 26) dobivamo broj jednak vremenu (periodu) revolucije planeta Plutona oko Sunca u sekundama (s); " Ovaj broj je»: 7880889600 s. U odgovorima je označeno slovom "u".

Prilikom rješavanja zadataka upišite brojeve u ćelije tablice olovkom.

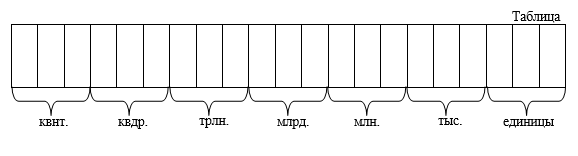
Fasetni test. Izmisli broj

Tablica sadrži brojeve:

Ako a

1) uzmite broj (brojeve) iz tablice:

2) 4; 3) 5; 4) 7; 5) 8; 6) 9;

7) smjestiti ovu brojku (brojeve) u kategoriju (znamenke);

8) stotine kvadrilijuna i desetke kvadrilijuna;

9) deseci milijuna;

10) stotine milijuna;

11) milijarda;

12) kvintilijuni;

13) desetke kvintilijuna;

14) stotine kvintilijuna;

15) bilijun;

16) stotine tisuća;

17) desetci tisuća;

18) popuniti razred (razrede) s njom (njima);

19) kvintilijuni;

20) milijarda;

21) popunite preostale znamenke nulama;

22) smjestiti brojeve 9 i 6 na tisućitnice i stotice;

23) dobivamo broj jednak masi Zemlje u desecima tona;

24) dobivamo broj približno jednak volumenu Zemlje u kubnim metrima;

25) dobivamo broj jednak udaljenosti (u metrima) od Sunca do najudaljenijeg planeta Sunčevog sustava Plutona;

26) dobivamo broj jednak vremenu (periodu) revolucije planeta Plutona oko Sunca u sekundama (s);

Ovaj broj je:

a) 5929000000000

b) 999990000000000000000

d) 59800000000000000000

Riješiti probleme:

1, 3, 6, 5, 18, 19, 21, 23

1, 6, 7, 14, 13, 12, 8, 21, 24

1, 4, 7, 11, 1, 5, 7, 10, 9, 16, 17, 22, 21, 26

1, 3, 7, 15, 1, 6, 2, 6, 18, 20, 21, 25

Odgovori

1, 3, 6, 5, 18, 19, 21, 23 - g

1, 6, 7, 14, 13, 12, 8, 21, 24 - b

1, 4, 7, 11, 1, 5, 7, 10, 9, 16, 17, 22, 21, 26 - u

1, 3, 7, 15, 1, 6, 2, 6, 18, 20, 21, 25 - a

U matematici postoji nekoliko različitih skupova brojeva: realni, kompleksni, cijeli, racionalni, iracionalni, ... U našem Svakidašnjica najčešće koristimo prirodne brojeve, jer ih susrećemo pri brojanju i traženju, označavajući broj predmeta.

U kontaktu s

Koji se brojevi nazivaju prirodnim

Od deset znamenki možete zapisati apsolutno bilo koji postojeći zbroj klasa i činova. Prirodne vrijednosti su one koji se koriste:

• Kada brojite bilo koje stavke (prvi, drugi, treći, ... peti, ... deseti).
• Kod označavanja broja predmeta (jedan, dva, tri...)

N vrijednosti su uvijek cijeli i pozitivni. Ne postoji najveći N, budući da skup cjelobrojnih vrijednosti nije ograničen.

Pažnja! Prirodni brojevi se dobivaju prebrojavanjem predmeta ili označavanjem njihove količine.

Apsolutno bilo koji broj može se rastaviti i prikazati kao bitni članovi, na primjer: 8.346.809=8 milijuna+346 tisuća+809 jedinica.

Postavite N

Skup N je u skupu realni, cijeli i pozitivni. U dijagramu skupova oni bi bili jedni u drugima, budući da je skup prirodnih dio njih.

Skup prirodnih brojeva označava se slovom N. Taj skup ima početak, ali nema kraj.

Postoji i prošireni skup N, gdje je uključena nula.

najmanji prirodni broj

U većini matematičkih škola najmanja vrijednost N računati kao jedinica, budući da se odsutnost objekata smatra praznim.

Ali u stranim matematičkim školama, na primjer, na francuskom, smatra se prirodnim. Prisutnost nule u nizu olakšava dokaz neki teoremi.

Skup vrijednosti N koji uključuje nulu naziva se proširenim i označava se simbolom N0 (nulti indeks).

Nizovi prirodnih brojeva

N redaka je niz svih N skupova znamenki. Ovaj niz nema kraja.

Osobitost prirodnog niza je da će se sljedeći broj razlikovati za jedan od prethodnog, odnosno povećavati. Ali značenja ne može biti negativan.

Pažnja! Radi lakšeg brojanja postoje klase i kategorije:

• Jedinice (1, 2, 3),
• desetice (10, 20, 30),
• Stotine (100, 200, 300),
• Tisuće (1000, 2000, 3000),
• Deseci tisuća (30.000),
• Stotine tisuća (800.000),
• Milijuni (4000000) itd.

Svi N

Svi N su u skupu realnih, cijelih, nenegativnih vrijednosti. Oni su njihovi sastavni dio.

Ove vrijednosti idu u beskonačnost, mogu pripadati klasama milijuna, milijardi, kvintilijuna itd.

Na primjer:

• Pet jabuka, tri mačića,
• Deset rubalja, trideset olovaka,
• Sto kilograma, tri stotine knjiga,
• Milijun zvijezda, tri milijuna ljudi itd.

Sekvenca u N

U različitim matematičkim školama mogu se naći dva intervala kojima niz N pripada:

od nule do plus beskonačno, uključujući krajeve, i od jedan do plus beskonačno, uključujući krajeve, to jest sve pozitivni cjeloviti odgovori.

N skupova znamenki mogu biti parni ili neparni. Razmotrite koncept neobičnosti.

Neparni (bilo koji neparni završavaju brojevima 1, 3, 5, 7, 9.) s dva imaju ostatak. Na primjer, 7:2=3,5, 11:2=5,5, 23:2=11,5.

Što čak znači N?

Svi parni zbroji klasa završavaju brojevima: 0, 2, 4, 6, 8. Kod dijeljenja parnog N s 2 neće biti ostatka, odnosno rezultat je cijeli odgovor. Na primjer, 50:2=25, 100:2=50, 3456:2=1728.

Važno! Numerički niz od N ne može se sastojati samo od parnih ili neparnih vrijednosti, jer se one moraju izmjenjivati: nakon parnog broja uvijek slijedi neparan broj, zatim opet paran broj, i tako dalje.

N svojstva

Kao i svi drugi skupovi, N ima svoja posebna svojstva. Razmotrimo svojstva niza N (neproširenog).

• Vrijednost koja je najmanja i koja ne slijedi nijednu drugu je jedan.
• N su niz, tj. jedna prirodna vrijednost slijedi drugi(osim jednog - to je prvi).
• Kada izvodimo računske operacije na N zbrojeva znamenki i klasa (zbrajanje, množenje), tada je odgovor uvijek ispadne prirodno značenje.
• U izračunima možete koristiti permutaciju i kombinaciju.
• Svaka sljedeća vrijednost ne može biti manja od prethodne. Također u nizu N djelovat će sljedeći zakon: ako je broj A manji od B, tada će u nizu brojeva uvijek postojati C, za koji vrijedi jednakost: A + C \u003d B.
• Ako uzmemo dva prirodna izraza, na primjer, A i B, tada će jedan od izraza biti istinit za njih: A \u003d B, A je veći od B, A je manji od B.
• Ako je A manje od B i B je manje od C, onda slijedi da da je A manje od C.
• Ako je A manji od B, onda slijedi da: ako im dodamo isti izraz (C), tada je A + C manji od B + C. Također je istina da ako se te vrijednosti pomnože s C, tada je AC manji od AB.
• Ako je B veći od A, ali manji od C, tada je B-A manji od C-A.

Pažnja! Sve navedene nejednakosti vrijede iu suprotnom smjeru.

Kako se zovu komponente množenja?

U mnogim jednostavnim, pa čak i složenim zadacima, pronalaženje odgovora ovisi o sposobnosti učenika.

Da biste brzo i ispravno množili i mogli rješavati inverzne zadatke, morate poznavati komponente množenja.

15. 10=150. U ovom izrazu, 15 i 10 su faktori, a 150 je proizvod.

Množenje ima svojstva koja su neophodna pri rješavanju problema, jednadžbi i nejednakosti:

• Preuređivanje faktora ne mijenja konačni proizvod.
• Da biste pronašli nepoznati faktor, morate umnožak podijeliti s poznatim faktorom (vrijedi za sve faktore).

Na primjer: 15 . X=150. Podijelite umnožak s poznatim faktorom. 150:15=10. Napravimo provjeru. petnaest . 10=150. Prema ovom principu čak složene linearne jednadžbe(ako ih pojednostavite).

Važno! Proizvod se može sastojati od više od samo dva faktora. Na primjer: 840=2 . 5. 7. 3. 4

Što su prirodni brojevi u matematici?

Pražnjenja i klase prirodnih brojeva

Zaključak

Sažmimo. N se koristi pri brojanju ili označavanju broja predmeta. Broj prirodnih skupova znamenki je beskonačan, ali uključuje samo cjelobrojne i pozitivne zbrojeve znamenki i klasa. Množenje je također potrebno za brojati stvari, kao i za rješavanje zadataka, jednadžbi i raznih nejednadžbi.

Matematika je nastala iz opće filozofije oko šestog stoljeća pr. e., i od tog trenutka je započeo njen pobjednički pohod svijetom. Svaki stupanj razvoja donosio je nešto novo – elementarno brojanje se razvijalo, transformiralo u diferencijalni i integralni račun, stoljeća su se smjenjivala, formule su postajale sve zbunjujuće i došao je trenutak kada je “počela najsloženija matematika – iz nje su nestali svi brojevi”. Ali što je bila osnova?

Početak vremena

Prirodni brojevi pojavili su se zajedno s prvim matematičkim operacijama. Jednom kralježnica, dvije kralježnice, tri kralježnice ... Pojavile su se zahvaljujući indijskim znanstvenicima koji su izveli prvi položajni

Riječ "pozicionalnost" znači da je mjesto svake znamenke u broju strogo definirano i odgovara njegovoj kategoriji. Na primjer, brojevi 784 i 487 su isti brojevi, ali brojevi nisu ekvivalentni, jer prvi uključuje 7 stotina, a drugi samo 4. Arapi su preuzeli inovaciju Indijaca, koji su brojeve doveli u oblik da sada znamo.

U davna vremena brojevima se pridavalo mistično značenje, Pitagora je vjerovao da je broj u osnovi stvaranja svijeta zajedno s glavnim elementima - vatrom, vodom, zemljom, zrakom. Ako sve promatramo samo s matematičke strane, što je onda prirodni broj? Polje prirodnih brojeva označava se s N i beskonačan je niz brojeva koji su cijeli i pozitivni: 1, 2, 3, … + ∞. Nula je isključena. Uglavnom se koristi za brojanje stavki i označavanje redoslijeda.

Što je u matematici? Peanovi aksiomi

Polje N je osnovno polje na koje se oslanja elementarna matematika. Tijekom vremena, polja cijelih brojeva, racionalnih,

Djelo talijanskog matematičara Giuseppea Peana omogućilo je daljnje strukturiranje aritmetike, postiglo njezinu formalnost i utrlo put daljnjim zaključcima koji su nadilazili polje N.

Što je prirodni broj razjašnjeno je ranije jednostavnim jezikom, u nastavku ćemo razmotriti matematičku definiciju temeljenu na Peanovim aksiomima.

• Jedan se smatra prirodnim brojem.
• Broj koji slijedi iza prirodnog broja je prirodan broj.
• Prije jedan nema prirodnog broja.
• Ako broj b slijedi i iza broja c i iza broja d, tada je c=d.
• Aksiom indukcije, koji pak pokazuje što je prirodni broj: ako je neka tvrdnja koja ovisi o parametru istinita za broj 1, tada pretpostavljamo da vrijedi i za broj n iz polja prirodnih brojeva N. Tada tvrdnja vrijedi i za n =1 iz polja prirodnih brojeva N.

Osnovne operacije za polje prirodnih brojeva

Budući da je polje N postalo prvo za matematičke izračune, na njega se odnose i domene definicije i rasponi vrijednosti niza operacija u nastavku. Zatvoreni su i nisu. Glavna razlika je u tome što će zatvorene operacije zajamčeno ostaviti rezultat unutar skupa N, bez obzira o kojim se brojevima radi. Dovoljno je da su prirodni. Ishod preostalih numeričkih interakcija više nije tako jednoznačan i izravno ovisi o vrsti brojeva koji su uključeni u izraz, budući da može proturječiti glavnoj definiciji. Dakle, zatvorene operacije:

• zbrajanje - x + y = z, gdje su x, y, z uključeni u polje N;
• množenje - x * y = z, gdje su x, y, z uključeni u polje N;
• stepenovanje - x y , gdje su x, y uključeni u polje N.

Preostale operacije, čiji rezultat možda ne postoji u kontekstu definicije "što je prirodni broj", su sljedeće:

Svojstva brojeva koji pripadaju polju N

Sva daljnja matematička razmišljanja temeljit će se na sljedećim svojstvima, najtrivijalnijim, ali ne manje važnim.

• Komutativno svojstvo zbrajanja je x + y = y + x, gdje su brojevi x, y uključeni u polje N. Ili dobro poznato "zbroj se ne mijenja promjenom mjesta članova."
• Komutativno svojstvo množenja je x * y = y * x, gdje su brojevi x, y uključeni u polje N.
• Asocijativno svojstvo zbrajanja je (x + y) + z = x + (y + z), gdje su x, y, z uključeni u polje N.
• Asocijativno svojstvo množenja je (x * y) * z = x * (y * z), gdje su brojevi x, y, z uključeni u polje N.
• svojstvo distribucije - x (y + z) = x * y + x * z, gdje su brojevi x, y, z uključeni u polje N.

Pitagorina tablica

Jedan od prvih koraka u poznavanju cjelokupne strukture elementarne matematike od strane školaraca, nakon što su sami shvatili koji se brojevi nazivaju prirodnim, je Pitagorina tablica. Može se smatrati ne samo sa znanstvenog stajališta, već i vrijednim znanstvenim spomenikom.

Ova tablica množenja je tijekom vremena doživjela niz promjena: iz nje je uklonjena nula, a brojevi od 1 do 10 označavaju sami sebe, ne uzimajući u obzir redoslijede (stotice, tisuće ...). To je tablica u kojoj su naslovi redaka i stupaca brojevi, a sadržaj ćelija njihovog presjeka jednak je njihovom umnošku.

U nastavnoj praksi posljednjih desetljeća javlja se potreba učenja Pitagorine tablice napamet „po redu“, odnosno učenje napamet ide prvo. Množenje s 1 je isključeno jer je rezultat bio 1 ili veći. U međuvremenu, u tablici golim okom možete vidjeti uzorak: umnožak brojeva raste za jedan korak, što je jednako naslovu retka. Dakle, drugi faktor nam pokazuje koliko puta trebamo uzeti prvi da bismo dobili željeni proizvod. Ovaj je sustav puno praktičniji od onog koji se prakticirao u srednjem vijeku: čak i shvaćajući što je prirodni broj i koliko je trivijalan, ljudi su uspjeli zakomplicirati svoje svakodnevno brojanje koristeći sustav temeljen na potencijama dvojke.

Podskup kao kolijevka matematike

Trenutno se polje prirodnih brojeva N smatra samo jednim od podskupova kompleksnih brojeva, ali to ih ne čini manje vrijednima u znanosti. Prirodni broj je prva stvar koju dijete nauči proučavajući sebe i svijet oko sebe. Jedan prst, dva prsta ... Zahvaljujući njemu, osoba razvija logično razmišljanje, kao i sposobnost utvrđivanja uzroka i zaključivanja posljedice, utirući put velikim otkrićima.

Prirodni brojevi jedan su od najstarijih matematičkih pojmova.

U dalekoj prošlosti ljudi nisu poznavali brojeve, a kada su trebali prebrojati predmete (životinje, ribe i sl.), radili su to drugačije nego mi sada.

Broj predmeta uspoređivali su s dijelovima tijela, na primjer, s prstima na ruci i govorili: "Imam onoliko oraha koliko ima prstiju na ruci."

S vremenom su ljudi shvatili da pet oraha, pet koza i pet zečeva imaju zajedničko svojstvo - njihov broj je pet.

Zapamtiti!

Cijeli brojevi su brojevi, počevši od 1, dobiveni prilikom prebrojavanja predmeta.

1, 2, 3, 4, 5…

najmanji prirodni broj — 1 .

najveći prirodni broj ne postoji.

Pri brojanju se ne koristi broj nula. Stoga se nula ne smatra prirodnim brojem.

Ljudi su mnogo kasnije naučili pisati brojeve nego brojati. Prije svega, počeli su predstavljati jedinicu s jednim štapom, zatim s dva štapa - brojem 2, s tri - brojem 3.

| — 1, || — 2, ||| — 3, ||||| — 5 …

Zatim su se pojavili posebni znakovi za označavanje brojeva - preteče modernih brojeva. Brojevi koje koristimo za pisanje brojeva potječu iz Indije prije otprilike 1500 godina. Arapi su ih donijeli u Europu, tako se i zovu arapski brojevi.

Ukupno ima deset znamenki: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Ove znamenke se mogu koristiti za pisanje bilo kojeg prirodnog broja.

Zapamtiti!

prirodne serije je niz svih prirodnih brojeva:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …

U prirodnom nizu svaki broj je veći od prethodnog za 1.

Prirodni niz je beskonačan, u njemu ne postoji najveći prirodni broj.

Sustav brojanja koji koristimo zove se decimalni pozicijski.

Decimala jer 10 jedinica svake znamenke čini 1 jedinicu najznačajnije znamenke. Pozicijski jer vrijednost znamenke ovisi o njezinu mjestu u zapisu broja, odnosno o znamenki kojom je zapisana.

Važno!

Klase iza milijarde nazvane su prema latinskim nazivima brojeva. Svaka sljedeća jedinica sadrži tisuću prethodnih.

• 1.000 milijardi = 1.000.000.000.000 = 1 trilijun ("tri" je latinski za "tri")
• 1.000 trilijuna = 1.000.000.000.000.000 = 1 kvadrilijun ("quadra" je latinski za "četiri")
• 1.000 kvadrilijuna = 1.000.000.000.000.000.000 = 1 kvintilijun ("kvinta" je latinski za "pet")

Međutim, fizičari su pronašli broj koji premašuje broj svih atoma (najsitnijih čestica materije) u cijelom svemiru.

Ovaj broj ima poseban naziv - googol. Googol je broj koji ima 100 nula.