टेलर श्रृंखला में कॉस का विस्तार। पावर श्रृंखला में कार्यों का विस्तार
16.1. टेलर श्रृंखला में प्राथमिक कार्यों का विस्तार और
मक्लौरिन
आइए हम दिखाते हैं कि यदि सेट पर एक मनमाना फ़ंक्शन परिभाषित किया गया है  , बिंदु के आसपास के क्षेत्र में
, बिंदु के आसपास के क्षेत्र में  इसके कई व्युत्पन्न हैं और यह एक घात श्रृंखला का योग है:
इसके कई व्युत्पन्न हैं और यह एक घात श्रृंखला का योग है:
तो आप इस श्रृंखला के गुणांक पा सकते हैं।
एक शक्ति श्रृंखला में स्थानापन्न  . तब
. तब  .
.
फ़ंक्शन का पहला व्युत्पन्न खोजें  :
:
पर  :
: .
.
दूसरे व्युत्पन्न के लिए हमें मिलता है:
पर  :
: .
.
यह प्रक्रिया जारी है एनएक बार हमें मिल जाए:  .
.
इस प्रकार, हमें फॉर्म की एक शक्ति श्रृंखला मिली:


 ,
,
जिसे कहा जाता है टेलर के पाससमारोह के लिए  बिंदु के आसपास
बिंदु के आसपास  .
.
टेलर श्रृंखला का एक विशेष मामला है मैकलॉरिन श्रृंखलापर  :
:



टेलर (मैकलॉरिन) श्रृंखला का शेष भाग मुख्य श्रृंखला को हटाकर प्राप्त किया जाता है एनप्रथम पद और के रूप में दर्शाया गया है  . फिर फ़ंक्शन
. फिर फ़ंक्शन  योग के रूप में लिखा जा सकता है एनश्रृंखला के पहले सदस्य
योग के रूप में लिखा जा सकता है एनश्रृंखला के पहले सदस्य  और शेष
और शेष  :,
:,
 .
.
बाकी तो आमतौर पर है  विभिन्न सूत्रों में व्यक्त किया गया है।
विभिन्न सूत्रों में व्यक्त किया गया है।
उनमें से एक लैग्रेंज रूप में है:
 , कहाँ
, कहाँ  .
. .
.
ध्यान दें कि व्यवहार में मैकलॉरिन श्रृंखला का प्रयोग अधिक बार किया जाता है। इस प्रकार, फ़ंक्शन लिखने के लिए  घात श्रृंखला के योग के रूप में, यह आवश्यक है:
घात श्रृंखला के योग के रूप में, यह आवश्यक है:
1) मैकलॉरिन (टेलर) श्रृंखला के गुणांक ज्ञात करें;
2) परिणामी शक्ति श्रृंखला के अभिसरण का क्षेत्र ज्ञात करें;
3) सिद्ध करें कि दी गई श्रृंखला फ़ंक्शन में परिवर्तित होती है  .
.
प्रमेय1
(मैकलॉरिन श्रृंखला के अभिसरण के लिए एक आवश्यक और पर्याप्त शर्त)। मान लीजिए श्रृंखला की अभिसरण त्रिज्या है  . इस श्रृंखला को अंतराल में अभिसरण करने के लिए
. इस श्रृंखला को अंतराल में अभिसरण करने के लिए  कार्य करने के लिए
कार्य करने के लिए  , यह आवश्यक और पर्याप्त है कि निम्नलिखित शर्त पूरी हो:
, यह आवश्यक और पर्याप्त है कि निम्नलिखित शर्त पूरी हो:  निर्दिष्ट अंतराल के भीतर.
निर्दिष्ट अंतराल के भीतर.
प्रमेय 2.यदि किसी फ़ंक्शन के किसी क्रम का व्युत्पन्न  कुछ अंतराल में
कुछ अंतराल में  पूर्ण मान में समान संख्या तक सीमित एम, वह है
पूर्ण मान में समान संख्या तक सीमित एम, वह है  , फिर इस अंतराल में फ़ंक्शन
, फिर इस अंतराल में फ़ंक्शन  मैकलॉरिन श्रृंखला में विस्तारित किया जा सकता है।
मैकलॉरिन श्रृंखला में विस्तारित किया जा सकता है।
उदाहरण1
.
बिंदु के चारों ओर टेलर श्रृंखला में विस्तार करें  समारोह।
समारोह।
समाधान।
 .
.
 ,;
,;
 ,
, ;
;
 ,
, ;
;
 ,
,
.......................................................................................................................................
 ,
, ;
;
अभिसरण क्षेत्र  .
.
उदाहरण2
.
फ़ंक्शन का विस्तार करें  टेलर श्रृंखला में एक बिंदु के आसपास
टेलर श्रृंखला में एक बिंदु के आसपास  .
.
समाधान:
हम फ़ंक्शन और उसके डेरिवेटिव का मान पाते हैं  .
.
 ,
, ;
;
 ,
, ;
;
...........……………………………
 ,
, .
.
इन मानों को एक पंक्ति में रखें। हम पाते हैं:
या  .
.
आइए इस श्रृंखला के अभिसरण का क्षेत्र ज्ञात करें। डी'अलेम्बर्ट परीक्षण के अनुसार, श्रृंखला अभिसरण करती है यदि
 .
.
इसलिए, किसी के लिए  यह सीमा 1 से कम है, और इसलिए श्रृंखला के अभिसरण का क्षेत्र होगा:
यह सीमा 1 से कम है, और इसलिए श्रृंखला के अभिसरण का क्षेत्र होगा:  .
.
आइए बुनियादी प्राथमिक कार्यों की मैकलॉरिन श्रृंखला में विस्तार के कई उदाहरणों पर विचार करें। मैकलॉरिन श्रृंखला को याद करें:


 .
.
अंतराल पर एकत्रित होता है  कार्य करने के लिए
कार्य करने के लिए  .
.
ध्यान दें कि फ़ंक्शन को एक श्रृंखला में विस्तारित करने के लिए, यह आवश्यक है:
ए) किसी दिए गए फ़ंक्शन के लिए मैकलॉरिन श्रृंखला के गुणांक खोजें;
बी) परिणामी श्रृंखला के लिए अभिसरण की त्रिज्या की गणना करें;
ग) साबित करें कि परिणामी श्रृंखला फ़ंक्शन में परिवर्तित हो जाती है  .
.
उदाहरण 3फ़ंक्शन पर विचार करें  .
.
समाधान।
आइए हम फ़ंक्शन और उसके डेरिवेटिव के मान की गणना करें  .
.
तब श्रृंखला के संख्यात्मक गुणांक का रूप होता है:
किसी के लिए भी एन।हम मैकलॉरिन श्रृंखला में पाए गए गुणांकों को प्रतिस्थापित करते हैं और प्राप्त करते हैं: 
परिणामी श्रृंखला के अभिसरण की त्रिज्या ज्ञात कीजिए, अर्थात्:
 .
.
इसलिए, श्रृंखला अंतराल पर अभिसरण करती है  .
.
यह शृंखला फ़ंक्शन में परिवर्तित हो जाती है  किसी भी मान के लिए
किसी भी मान के लिए  , क्योंकि किसी भी अंतराल पर
, क्योंकि किसी भी अंतराल पर  समारोह
समारोह  और इसके निरपेक्ष मूल्य व्युत्पन्न संख्या द्वारा सीमित हैं
और इसके निरपेक्ष मूल्य व्युत्पन्न संख्या द्वारा सीमित हैं  .
.
उदाहरण4
.
फ़ंक्शन पर विचार करें  .
.
समाधान.
 :
:

यह देखना आसान है कि सम-क्रम व्युत्पन्न  , और विषम क्रम के व्युत्पन्न। हम मैकलॉरिन श्रृंखला में पाए गए गुणांकों को प्रतिस्थापित करते हैं और विस्तार प्राप्त करते हैं:
, और विषम क्रम के व्युत्पन्न। हम मैकलॉरिन श्रृंखला में पाए गए गुणांकों को प्रतिस्थापित करते हैं और विस्तार प्राप्त करते हैं:
आइए इस श्रृंखला के अभिसरण का अंतराल ज्ञात करें। डी'अलेम्बर्ट के अनुसार:
किसी के लिए भी  . इसलिए, श्रृंखला अंतराल पर अभिसरण करती है
. इसलिए, श्रृंखला अंतराल पर अभिसरण करती है  .
.
यह शृंखला फ़ंक्शन में परिवर्तित हो जाती है  , क्योंकि इसके सभी व्युत्पन्न एक तक ही सीमित हैं।
, क्योंकि इसके सभी व्युत्पन्न एक तक ही सीमित हैं।
उदाहरण5
.
 .
.
समाधान।
आइए हम फ़ंक्शन और उसके डेरिवेटिव का मान ज्ञात करें  :
:

इस प्रकार, इस श्रृंखला के गुणांक:  और
और  , इस तरह:
, इस तरह:
इसी प्रकार पिछली श्रृंखला के साथ, अभिसरण का क्षेत्र  . श्रृंखला फ़ंक्शन में परिवर्तित हो जाती है
. श्रृंखला फ़ंक्शन में परिवर्तित हो जाती है  , क्योंकि इसके सभी व्युत्पन्न एक तक ही सीमित हैं।
, क्योंकि इसके सभी व्युत्पन्न एक तक ही सीमित हैं।
ध्यान दें कि फ़ंक्शन  विषम शक्तियों में विषम और श्रृंखला विस्तार, कार्य
विषम शक्तियों में विषम और श्रृंखला विस्तार, कार्य  – सम और सम घातों में एक शृंखला में विस्तार।
– सम और सम घातों में एक शृंखला में विस्तार।
उदाहरण6
.
द्विपद श्रृंखला:  .
.
समाधान.
आइए हम फ़ंक्शन और उसके डेरिवेटिव का मान ज्ञात करें  :
:

इससे पता चलता है कि:

हम गुणांकों के इन मानों को मैकलॉरिन श्रृंखला में प्रतिस्थापित करते हैं और एक शक्ति श्रृंखला में इस फ़ंक्शन का विस्तार प्राप्त करते हैं:
आइए इस श्रृंखला के अभिसरण की त्रिज्या ज्ञात करें:

इसलिए, श्रृंखला अंतराल पर अभिसरण करती है  . सीमा बिंदुओं पर
. सीमा बिंदुओं पर  और
और  घातांक के आधार पर श्रृंखला अभिसरित हो भी सकती है और नहीं भी
घातांक के आधार पर श्रृंखला अभिसरित हो भी सकती है और नहीं भी  .
.
अध्ययन की गई श्रृंखला अंतराल पर अभिसरण करती है  कार्य करने के लिए
कार्य करने के लिए  , अर्थात् श्रृंखला का योग
, अर्थात् श्रृंखला का योग  पर
पर  .
.
उदाहरण7
.
आइए मैकलॉरिन श्रृंखला में फ़ंक्शन का विस्तार करें  .
.
समाधान।
इस फ़ंक्शन को एक श्रृंखला में विस्तारित करने के लिए, हम द्विपद श्रृंखला का उपयोग करते हैं  . हम पाते हैं:
. हम पाते हैं: 
शक्ति श्रृंखला की संपत्ति के आधार पर (एक शक्ति श्रृंखला को इसके अभिसरण के क्षेत्र में एकीकृत किया जा सकता है), हम इस श्रृंखला के बाएं और दाएं भागों का अभिन्न अंग पाते हैं:
इस श्रृंखला का अभिसरण क्षेत्र ज्ञात कीजिये:  ,
,
अर्थात् इस श्रृंखला का अभिसरण क्षेत्र अंतराल है  . आइए हम अंतराल के अंत में श्रृंखला के अभिसरण का निर्धारण करें। पर
. आइए हम अंतराल के अंत में श्रृंखला के अभिसरण का निर्धारण करें। पर 
 . यह श्रृंखला एक हार्मोनिक श्रृंखला है, अर्थात यह अपसरण करती है। पर
. यह श्रृंखला एक हार्मोनिक श्रृंखला है, अर्थात यह अपसरण करती है। पर  हमें एक सामान्य पद वाली एक संख्या श्रृंखला मिलती है
हमें एक सामान्य पद वाली एक संख्या श्रृंखला मिलती है  .
.
लीबनिज़ श्रृंखला अभिसरण करती है। इस प्रकार, इस श्रृंखला का अभिसरण क्षेत्र अंतराल है  .
.
16.2. अनुमानित गणना में शक्तियों की शक्ति श्रृंखला का अनुप्रयोग
अनुमानित गणना में पावर श्रृंखला अत्यंत महत्वपूर्ण भूमिका निभाती है। उनकी मदद से, त्रिकोणमितीय कार्यों की तालिकाएँ, लघुगणक की तालिकाएँ, ज्ञान के विभिन्न क्षेत्रों में उपयोग किए जाने वाले अन्य कार्यों के मूल्यों की तालिकाएँ संकलित की गईं, उदाहरण के लिए, संभाव्यता सिद्धांत और गणितीय आँकड़ों में। इसके अतिरिक्त, किसी शक्ति श्रृंखला में कार्यों का विस्तार उनके सैद्धांतिक अध्ययन के लिए उपयोगी है। अनुमानित गणनाओं में पावर श्रृंखला का उपयोग करते समय मुख्य मुद्दा श्रृंखला के योग को उसके पहले के योग से प्रतिस्थापित करते समय त्रुटि का अनुमान लगाने का प्रश्न है एनसदस्य.
दो मामलों पर विचार करें:
फ़ंक्शन को एक वैकल्पिक श्रृंखला में विस्तारित किया गया है;
फ़ंक्शन को स्थिर-चिह्न श्रृंखला में विस्तारित किया गया है।
वैकल्पिक श्रृंखला का उपयोग करके गणना
कार्य करने दो  एक वैकल्पिक शक्ति श्रृंखला में विस्तारित। फिर, किसी विशिष्ट मान के लिए इस फ़ंक्शन की गणना करते समय
एक वैकल्पिक शक्ति श्रृंखला में विस्तारित। फिर, किसी विशिष्ट मान के लिए इस फ़ंक्शन की गणना करते समय  हमें एक संख्या श्रृंखला मिलती है जिस पर हम लाइबनिज परीक्षण लागू कर सकते हैं। इस मानदंड के अनुसार, यदि किसी श्रृंखला के योग को उसके पहले के योग से बदल दिया जाए एनसदस्य, तो पूर्ण त्रुटि इस श्रृंखला के शेष के पहले पद से अधिक नहीं है, अर्थात:
हमें एक संख्या श्रृंखला मिलती है जिस पर हम लाइबनिज परीक्षण लागू कर सकते हैं। इस मानदंड के अनुसार, यदि किसी श्रृंखला के योग को उसके पहले के योग से बदल दिया जाए एनसदस्य, तो पूर्ण त्रुटि इस श्रृंखला के शेष के पहले पद से अधिक नहीं है, अर्थात:  .
.
उदाहरण8
.
गणना  0.0001 की सटीकता के साथ।
0.0001 की सटीकता के साथ।
समाधान.
हम मैकलॉरिन श्रृंखला का उपयोग करेंगे  , कोण का मान रेडियन में प्रतिस्थापित करने पर:
, कोण का मान रेडियन में प्रतिस्थापित करने पर:

यदि हम दी गई सटीकता के साथ श्रृंखला के पहले और दूसरे सदस्यों की तुलना करते हैं, तो:।
तीसरा विस्तार पद:
निर्दिष्ट गणना सटीकता से कम। इसलिए, गणना करने के लिए  यह श्रृंखला के दो पदों को छोड़ने के लिए पर्याप्त है, अर्थात
यह श्रृंखला के दो पदों को छोड़ने के लिए पर्याप्त है, अर्थात
 .
.
इस प्रकार  .
.
उदाहरण9
.
गणना  0.001 की सटीकता के साथ.
0.001 की सटीकता के साथ.
समाधान.
हम द्विपद श्रृंखला सूत्र का उपयोग करेंगे। इसके लिए हम लिखते हैं  जैसा:
जैसा:  .
.
इस अभिव्यक्ति में  ,
,

आइए श्रृंखला के प्रत्येक पद की दी गई सटीकता से तुलना करें। यह स्पष्ट है कि  . इसलिए, गणना करने के लिए
. इसलिए, गणना करने के लिए  श्रृंखला के तीन सदस्यों को छोड़ना पर्याप्त है।
श्रृंखला के तीन सदस्यों को छोड़ना पर्याप्त है।
 या
या  .
.
साइन-पॉजिटिव श्रृंखला का उपयोग करके गणना
उदाहरण10
.
संख्या की गणना करें  0.001 की सटीकता के साथ.
0.001 की सटीकता के साथ.
समाधान.
किसी समारोह के लिए एक पंक्ति में  विकल्प
विकल्प  . हम पाते हैं:
. हम पाते हैं:

आइए उस त्रुटि का अनुमान लगाएं जो तब उत्पन्न होती है जब श्रृंखला का योग पहली श्रृंखला के योग से बदल दिया जाता है  सदस्य. आइए स्पष्ट असमानता को लिखें:
सदस्य. आइए स्पष्ट असमानता को लिखें:
यानी 2< <3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
<3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
 ,
, .
.
समस्या की स्थिति के अनुसार आपको ढूंढना होगा एनजैसे कि निम्नलिखित असमानता कायम है:  या
या  .
.
यह जांचना आसान है कि कब एन= 6: .
.
इस तरह,  .
.
उदाहरण11
.
गणना  0.0001 की सटीकता के साथ।
0.0001 की सटीकता के साथ।
समाधान.
ध्यान दें कि लघुगणक की गणना करने के लिए, कोई फ़ंक्शन के लिए श्रृंखला लागू कर सकता है  , लेकिन यह श्रृंखला बहुत धीमी गति से अभिसरण करती है और दी गई सटीकता प्राप्त करने के लिए 9999 शब्दों का सहारा लेना होगा! इसलिए, लघुगणक की गणना करने के लिए, एक नियम के रूप में, फ़ंक्शन के लिए एक श्रृंखला का उपयोग किया जाता है
, लेकिन यह श्रृंखला बहुत धीमी गति से अभिसरण करती है और दी गई सटीकता प्राप्त करने के लिए 9999 शब्दों का सहारा लेना होगा! इसलिए, लघुगणक की गणना करने के लिए, एक नियम के रूप में, फ़ंक्शन के लिए एक श्रृंखला का उपयोग किया जाता है  , जो अंतराल पर एकत्रित होता है
, जो अंतराल पर एकत्रित होता है  .
.
गणना करना  इस पंक्ति के साथ. होने देना
इस पंक्ति के साथ. होने देना  , तब
, तब  .
.
इस तरह,  ,
,
गणना करने के लिए  दी गई सटीकता के साथ, पहले चार पदों का योग लें:
दी गई सटीकता के साथ, पहले चार पदों का योग लें:  .
.
शेष पंक्ति  खारिज करना। आइए त्रुटि का अनुमान लगाएं. यह तो स्पष्ट है
खारिज करना। आइए त्रुटि का अनुमान लगाएं. यह तो स्पष्ट है 
या  .
.

इस प्रकार, गणना के लिए जिस श्रृंखला का उपयोग किया गया था, उसमें फ़ंक्शन के लिए श्रृंखला में 9999 के बजाय केवल पहले चार पद लेने के लिए पर्याप्त था  .
.
स्व-निदान के लिए प्रश्न
1. टेलर श्रृंखला क्या है?
2. मैकलॉरिन की किस प्रकार की श्रृंखला थी?
3. टेलर श्रृंखला में किसी फ़ंक्शन के विस्तार पर एक प्रमेय तैयार करें।
4. मैकलॉरिन श्रृंखला के मुख्य कार्यों का विस्तार लिखिए।
5. विचाराधीन श्रृंखला के अभिसरण के क्षेत्रों को इंगित करें।
6. पावर श्रृंखला का उपयोग करके अनुमानित गणना में त्रुटि का अनुमान कैसे लगाएं?
यदि फ़ंक्शन f(x) में बिंदु a वाले कुछ अंतराल पर सभी आदेशों के व्युत्पन्न हैं, तो टेलर सूत्र को इस पर लागू किया जा सकता है:
,
कहाँ आर एन- तथाकथित अवशिष्ट पद या श्रृंखला का शेष, इसका अनुमान लैग्रेंज सूत्र का उपयोग करके लगाया जा सकता है:
, जहां संख्या x, x और a के बीच स्थित है।
फ़ंक्शन प्रविष्टि नियम:
यदि कुछ मूल्य के लिए एक्स आर एन→0 पर एन→∞, फिर सीमा में टेलर सूत्र इस मान के लिए अभिसरण में बदल जाता है टेलर श्रृंखला:
,
इस प्रकार, फ़ंक्शन f(x) को विचारित बिंदु x पर टेलर श्रृंखला में विस्तारित किया जा सकता है यदि:
1) इसमें सभी ऑर्डरों के डेरिवेटिव हैं;
2) निर्मित श्रृंखला इस बिंदु पर अभिसरण करती है।
a = 0 के लिए हमें एक श्रृंखला प्राप्त होती है जिसे कहा जाता है मैकलॉरिन के पास:
,
मैकलॉरिन श्रृंखला में सबसे सरल (प्राथमिक) कार्यों का विस्तार:
घातीय कार्य
, आर=∞
त्रिकोणमितीय कार्य ![]() , आर=∞
, आर=∞ ![]() , आर=∞
, आर=∞
, (-π/2< x < π/2), R=π/2
फ़ंक्शन actgx x की शक्तियों में विस्तारित नहीं होता है, क्योंकि ctg0=∞
अतिशयोक्तिपूर्ण कार्य
लघुगणकीय कार्य
, -1
द्विपद श्रृंखला
![]() .
.
उदाहरण 1। फ़ंक्शन को पावर श्रृंखला में विस्तारित करें एफ(एक्स)= 2एक्स.
समाधान. आइए हम फ़ंक्शन और उसके डेरिवेटिव के मान ज्ञात करें एक्स=0
एफ(एक्स) = 2एक्स, एफ( 0)
= 2 0
=1;
च"(x) = 2एक्सएलएन2, एफ"( 0)
= 2 0
ln2=ln2;
च""(x) = 2एक्सएलएन 2 2, एफ""( 0)
= 2 0
लॉग 2 2= लॉग 2 2;
…
एफ(एन)(एक्स) = 2एक्सएल.एन एन 2, एफ(एन)( 0)
= 2 0
एल.एन एन 2=एल.एन एन 2.
डेरिवेटिव के प्राप्त मूल्यों को टेलर श्रृंखला सूत्र में प्रतिस्थापित करने पर, हमें मिलता है:
इस श्रृंखला की अभिसरण त्रिज्या अनंत के बराबर है, इसलिए यह विस्तार -∞ के लिए मान्य है<एक्स<+∞.
उदाहरण #2. शक्तियों में एक टेलर श्रृंखला लिखें ( एक्स+4) फ़ंक्शन के लिए एफ(एक्स)=इ एक्स.
समाधान. फ़ंक्शन ई के व्युत्पन्न ढूँढना एक्सऔर बिंदु पर उनके मूल्य एक्स=-4.
एफ(एक्स)= ई एक्स, एफ(-4)
= ई -4
;
च"(x)= ई एक्स, एफ"(-4)
= ई -4
;
च""(x)= ई एक्स, एफ""(-4)
= ई -4
;
…
एफ(एन)(एक्स)= ई एक्स, एफ(एन)( -4)
= ई -4
.
इसलिए, फ़ंक्शन की वांछित टेलर श्रृंखला का रूप इस प्रकार है:
यह विस्तार -∞ के लिए भी मान्य है<एक्स<+∞.
उदाहरण #3. फ़ंक्शन का विस्तार करें एफ(एक्स)=एल.एन एक्सडिग्री द्वारा एक श्रृंखला में ( एक्स- 1),
(अर्थात बिंदु के आसपास टेलर श्रृंखला में एक्स=1).
समाधान. हम इस फ़ंक्शन के व्युत्पन्न पाते हैं।
f(x)=lnx , , , ,
f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f(n)=(- 1) एन-1 (एन-1)!
इन मानों को सूत्र में प्रतिस्थापित करने पर, हमें वांछित टेलर श्रृंखला प्राप्त होती है:
डी'एलेम्बर्ट के परीक्षण की सहायता से, कोई यह सत्यापित कर सकता है कि श्रृंखला ½x-1½ पर अभिसरण करती है<1 . Действительно,
यदि ½ हो तो श्रृंखला अभिसरित हो जाती है एक्स- 1½<1, т.е. при 0<एक्स<2. При एक्स=2 हमें एक वैकल्पिक श्रृंखला प्राप्त होती है जो लीबनिज परीक्षण की शर्तों को पूरा करती है। x=0 के लिए फ़ंक्शन परिभाषित नहीं है। इस प्रकार, टेलर श्रृंखला के अभिसरण का क्षेत्र अर्ध-खुला अंतराल (0;2] है।
उदाहरण #4. पावर श्रृंखला में फ़ंक्शन का विस्तार करें। उदाहरण संख्या 5. मैकलॉरिन श्रृंखला में फ़ंक्शन का विस्तार करें। टिप्पणी
.
यह विधि किसी शक्ति श्रृंखला में किसी फ़ंक्शन के विस्तार की विशिष्टता पर प्रमेय पर आधारित है। इस प्रमेय का सार यह है कि एक ही बिंदु के आसपास, दो अलग-अलग शक्ति श्रृंखलाएं प्राप्त नहीं की जा सकती हैं जो एक ही कार्य में परिवर्तित हो जाएंगी, चाहे इसका विस्तार कैसे भी किया जाए। उदाहरण संख्या 5ए. मैकलॉरिन श्रृंखला में फ़ंक्शन का विस्तार करें, अभिसरण के क्षेत्र को इंगित करें। भिन्न 3/(1-3x) को 3x के हर के साथ एक अनंत रूप से घटती ज्यामितीय प्रगति के योग के रूप में देखा जा सकता है यदि |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
उदाहरण संख्या 6. बिंदु x = 3 के आसपास टेलर श्रृंखला में फ़ंक्शन का विस्तार करें। उदाहरण संख्या 7. फ़ंक्शन ln(x+2) की शक्तियों (x -1) में एक टेलर श्रृंखला लिखें। उदाहरण संख्या 8. बिंदु x =2 के चारों ओर टेलर श्रृंखला में फ़ंक्शन f(x)=sin(πx/4) का विस्तार करें। उदाहरण 1। 0.01 के भीतर ln(3) की गणना करें। उदाहरण #2. निकटतम 0.0001 तक गणना करें। उदाहरण #3. 10 -5 के भीतर अभिन्न ∫ 0 1 4 पाप (x) x की गणना करें। उदाहरण #4. 0.001 के भीतर अभिन्न ∫ 0 1 4 e x 2 की गणना करें। व्यावहारिक कौशल के प्रशिक्षण के लिए साइट पर टेलर, मैकलॉरिन और लॉरेंट की एक श्रृंखला में एक फ़ंक्शन का विघटन। किसी फ़ंक्शन का यह श्रृंखला विस्तार गणितज्ञों को उसकी परिभाषा के क्षेत्र में किसी बिंदु पर फ़ंक्शन के अनुमानित मूल्य का अनुमान लगाने का विचार देता है। ब्रेडिस तालिका का उपयोग करने की तुलना में ऐसे फ़ंक्शन मान की गणना करना बहुत आसान है, जो कंप्यूटिंग के युग में बहुत पुराना हो चुका है। किसी फ़ंक्शन को टेलर श्रृंखला में विस्तारित करने का अर्थ है इस श्रृंखला के रैखिक कार्यों के सामने गुणांक की गणना करना और उसे सही रूप में लिखना। छात्र इन दोनों श्रृंखलाओं को भ्रमित करते हैं, समझ नहीं पाते कि सामान्य मामला क्या है और दूसरे का विशेष मामला क्या है। हम आपको एक बार और सभी के लिए याद दिलाते हैं, मैकलॉरिन श्रृंखला टेलर श्रृंखला का एक विशेष मामला है, यानी, यह टेलर श्रृंखला है, लेकिन बिंदु x = 0 पर। ज्ञात कार्यों के विस्तार के सभी संक्षिप्त रिकॉर्ड, जैसे ई ^एक्स, सिन(एक्स), कॉस(एक्स) और अन्य, ये टेलर श्रृंखला में विस्तार हैं, लेकिन तर्क के लिए बिंदु 0 पर हैं। एक जटिल तर्क के कार्यों के लिए, लॉरेंट श्रृंखला टीएफकेटी में सबसे आम समस्या है, क्योंकि यह दो-तरफा अनंत श्रृंखला का प्रतिनिधित्व करती है। यह दो पंक्तियों का योग है. हमारा सुझाव है कि आप साइट साइट पर सीधे अपघटन का एक उदाहरण देखें, किसी भी संख्या के साथ "उदाहरण" और फिर "समाधान" बटन पर क्लिक करके ऐसा करना बहुत आसान है। किसी फ़ंक्शन के श्रृंखला में इस विस्तार से प्रमुखीकरण श्रृंखला जुड़ी होती है, जो मूल फ़ंक्शन को ऑर्डिनेट अक्ष के साथ एक निश्चित क्षेत्र में सीमित करती है, यदि चर एब्सिस्सा क्षेत्र से संबंधित है। वेक्टर विश्लेषण की तुलना गणित के एक अन्य दिलचस्प अनुशासन से की जाती है। चूंकि प्रत्येक शब्द की जांच की आवश्यकता होती है, इसलिए प्रक्रिया के लिए बहुत समय की आवश्यकता होती है। किसी भी टेलर श्रृंखला को x0 को शून्य से प्रतिस्थापित करके मैकलॉरिन श्रृंखला के साथ जोड़ा जा सकता है, लेकिन मैकलॉरिन श्रृंखला के लिए, टेलर श्रृंखला का विपरीत प्रतिनिधित्व कभी-कभी स्पष्ट नहीं होता है। चाहे इसे इसके शुद्ध रूप में करने की आवश्यकता न हो, यह सामान्य आत्म-विकास के लिए दिलचस्प है। प्रत्येक लॉरेंट श्रृंखला z-a की पूर्णांक शक्तियों में दो-तरफा अनंत शक्ति श्रृंखला से मेल खाती है, दूसरे शब्दों में, समान टेलर प्रकार की एक श्रृंखला, लेकिन गुणांक की गणना में थोड़ा अलग है। हम कई सैद्धांतिक गणनाओं के बाद, लॉरेंट श्रृंखला के अभिसरण के क्षेत्र के बारे में थोड़ी देर बाद बात करेंगे। पिछली शताब्दी की तरह, किसी फ़ंक्शन का एक श्रृंखला में चरणबद्ध विस्तार केवल पदों को एक सामान्य हर तक कम करके ही प्राप्त किया जा सकता है, क्योंकि हर में फ़ंक्शन गैर-रैखिक होते हैं। कार्यात्मक मूल्य की अनुमानित गणना के लिए समस्याओं के निर्माण की आवश्यकता होती है। इस तथ्य के बारे में सोचें कि जब टेलर श्रृंखला का तर्क एक रैखिक चर होता है, तो विस्तार कई चरणों में होता है, लेकिन एक पूरी तरह से अलग तस्वीर, जब एक जटिल या गैर-रैखिक फ़ंक्शन विस्तारित फ़ंक्शन के तर्क के रूप में कार्य करता है, तो पावर श्रृंखला में ऐसे फ़ंक्शन का प्रतिनिधित्व करने की प्रक्रिया स्पष्ट है, क्योंकि, इस तरह से, गणना करना आसान है, यद्यपि अनुमानित, लेकिन परिभाषा के क्षेत्र के किसी भी बिंदु पर मूल्य, न्यूनतम त्रुटि के साथ जिसमें बहुत कम है आगे की गणना पर प्रभाव। यह मैकलॉरिन श्रृंखला पर भी लागू होता है। जब शून्य बिंदु पर फ़ंक्शन की गणना करना आवश्यक हो। हालाँकि, लॉरेंट श्रृंखला को यहाँ काल्पनिक इकाइयों के साथ एक समतल विस्तार द्वारा दर्शाया गया है। साथ ही, समग्र प्रक्रिया के दौरान समस्या का सही समाधान सफलता के बिना नहीं होगा। गणित में, यह दृष्टिकोण ज्ञात नहीं है, लेकिन यह वस्तुनिष्ठ रूप से मौजूद है। परिणामस्वरूप, आप तथाकथित बिंदुवार उपसमुच्चय के निष्कर्ष पर पहुंच सकते हैं, और एक श्रृंखला में किसी फ़ंक्शन के विस्तार में, आपको इस प्रक्रिया के लिए ज्ञात तरीकों को लागू करने की आवश्यकता है, जैसे डेरिवेटिव के सिद्धांत को लागू करना। एक बार फिर हम शिक्षक की सत्यता के प्रति आश्वस्त हैं, जिन्होंने कम्प्यूटेशनल गणना के परिणामों के बारे में अपनी धारणाएँ बनाईं। आइए ध्यान दें कि गणित के सभी सिद्धांतों के अनुसार प्राप्त टेलर श्रृंखला मौजूद है और संपूर्ण संख्यात्मक अक्ष पर परिभाषित है, हालांकि, वेबसाइट सेवा के प्रिय उपयोगकर्ता, मूल फ़ंक्शन के रूप को न भूलें, क्योंकि यह खराब हो सकता है प्रारंभ में फ़ंक्शन के डोमेन को सेट करना आवश्यक है, अर्थात, उन बिंदुओं को लिखना और आगे के विचारों से बाहर करना जिन पर फ़ंक्शन वास्तविक संख्याओं के डोमेन में परिभाषित नहीं है। यूं कहें तो यह समस्या को सुलझाने में आपकी शीघ्रता को दर्शाएगा। तर्क के शून्य मान के साथ मैकलॉरिन श्रृंखला का निर्माण जो कहा गया है उसका अपवाद नहीं होगा। उसी समय, किसी ने किसी फ़ंक्शन की परिभाषा के डोमेन को खोजने की प्रक्रिया को रद्द नहीं किया, और आपको इस गणितीय कार्रवाई को पूरी गंभीरता से लेना चाहिए। यदि लॉरेंट श्रृंखला में मुख्य भाग शामिल है, तो पैरामीटर "ए" को एक अलग एकवचन बिंदु कहा जाएगा, और लॉरेंट श्रृंखला को रिंग में विस्तारित किया जाएगा - यह इसके भागों के अभिसरण के क्षेत्रों का प्रतिच्छेदन है, जहां से संबंधित है प्रमेय का पालन होगा. लेकिन सब कुछ उतना कठिन नहीं है जितना एक अनुभवहीन छात्र को पहली नज़र में लग सकता है। केवल टेलर श्रृंखला का अध्ययन करने के बाद, कोई लॉरेंट श्रृंखला को आसानी से समझ सकता है - संख्याओं के स्थान के विस्तार के लिए एक सामान्यीकृत मामला। किसी फ़ंक्शन का श्रृंखला में कोई भी विस्तार केवल फ़ंक्शन के क्षेत्र में एक बिंदु पर ही किया जा सकता है। ऐसे कार्यों के गुणों को ध्यान में रखना चाहिए, उदाहरण के लिए, आवधिकता या अनंत भिन्नता। हमारा यह भी सुझाव है कि आप प्राथमिक कार्यों की टेलर श्रृंखला में तैयार विस्तार की तालिका का उपयोग करें, क्योंकि एक फ़ंक्शन को दर्जनों विभिन्न पावर श्रृंखलाओं द्वारा दर्शाया जा सकता है, जिसे हमारे ऑनलाइन कैलकुलेटर के उपयोग से देखा जा सकता है। मैकलॉरिन की ऑनलाइन श्रृंखला यह निर्धारित करना पहले से कहीं अधिक आसान है कि क्या आप अद्वितीय साइट सेवा का उपयोग करते हैं, आपको बस सही लिखित फ़ंक्शन दर्ज करना होगा और आपको प्रस्तुत उत्तर कुछ ही सेकंड में प्राप्त हो जाएगा, यह सटीक और एक मानक लिखित रूप में गारंटी दी जाएगी . आप शिक्षक को सौंपने के लिए परिणाम को तुरंत एक साफ प्रति में फिर से लिख सकते हैं। पहले रिंगों में विचाराधीन फ़ंक्शन की विश्लेषणात्मकता को निर्धारित करना सही होगा, और फिर स्पष्ट रूप से बताएं कि इसे ऐसे सभी रिंगों में लॉरेंट श्रृंखला में विस्तारित किया जा सकता है। एक महत्वपूर्ण क्षण नकारात्मक डिग्री वाले लॉरेंट श्रृंखला के सदस्यों की दृष्टि न खोना है। जितना हो सके इसी पर फोकस करें. किसी फ़ंक्शन को पूर्णांक घातों में एक श्रृंखला में विस्तारित करने पर लॉरेंट के प्रमेय का अच्छा उपयोग करें। कार्यात्मक श्रृंखला के सिद्धांत में, किसी फ़ंक्शन को श्रृंखला में विस्तारित करने के लिए समर्पित अनुभाग एक केंद्रीय स्थान रखता है। इस प्रकार, समस्या उत्पन्न होती है: किसी दिए गए फ़ंक्शन के लिए
ऐसी शक्ति श्रृंखला खोजना आवश्यक है जो कुछ अंतराल पर एकत्रित हुआ और उसका योग बराबर था इस कार्य को कहा जाता है किसी फ़ंक्शन को पावर श्रृंखला में विस्तारित करने की समस्या। किसी फ़ंक्शन को पावर श्रृंखला में विस्तारित करने के लिए एक आवश्यक शर्तक्या इसकी भिन्नता अनंत बार है - यह अभिसरण शक्ति श्रृंखला के गुणों से निम्नानुसार है। यह शर्त, एक नियम के रूप में, उनकी परिभाषा के क्षेत्र में प्राथमिक कार्यों के लिए संतुष्ट है। तो चलिए मान लेते हैं कि function चलिए मान लेते हैं कि function कहाँ ए 0 ,ए 1 ,ए 2 ,...,ए पी ,...
- अनिश्चित (अभी तक) गुणांक। आइए हम मान को समानता (*) में रखें एक्स = एक्स 0 ,
तो हम पाते हैं हम घात श्रृंखला (*) को पद दर पद विभेदित करते हैं और यहाँ डाल रहा हूँ एक्स = एक्स 0 ,
हम पाते हैं अगले विभेदन के साथ, हमें श्रृंखला प्राप्त होती है मान लिया जाये एक्स = एक्स 0 ,
हम पाते हैं बाद पी-गुना विभेदन हमें मिलता है अंतिम समानता में मानते हुए एक्स = एक्स 0 ,
हम पाते हैं तो गुणांक पाए जाते हैं जिसे एक पंक्ति (*) में प्रतिस्थापित करने पर, हमें प्राप्त होता है परिणामी श्रृंखला कहलाती है टेलर के पास
समारोह के लिए
इस प्रकार, हमने इसे स्थापित किया है यदि फ़ंक्शन को घातों (x - x) में घात श्रृंखला में विस्तारित किया जा सकता है 0 ), तो यह विस्तार अद्वितीय है और परिणामी श्रृंखला आवश्यक रूप से एक टेलर श्रृंखला है। ध्यान दें कि टेलर श्रृंखला किसी भी फ़ंक्शन के लिए प्राप्त की जा सकती है जिसमें बिंदु पर किसी भी क्रम का व्युत्पन्न होता है एक्स = एक्स 0 .
लेकिन इसका मतलब यह नहीं है कि फ़ंक्शन और परिणामी श्रृंखला के बीच एक समान चिह्न लगाया जा सकता है, अर्थात। कि श्रृंखला का योग मूल फलन के बराबर है। सबसे पहले, ऐसी समानता केवल अभिसरण के क्षेत्र में समझ में आ सकती है, और फ़ंक्शन के लिए प्राप्त टेलर श्रृंखला भिन्न हो सकती है, और दूसरी बात, यदि टेलर श्रृंखला अभिसरण करती है, तो इसका योग मूल फ़ंक्शन के साथ मेल नहीं खा सकता है। आइए एक कथन तैयार करें जिसकी सहायता से बताई गई समस्या का समाधान हो जाएगा। यदि फ़ंक्शन
कहाँआर एन (एक्स)-टेलर सूत्र का अवशिष्ट पद - का रूप है (लैग्रेंज रूप) कहाँ
डॉटξ
x और x के बीच स्थित है 0 . ध्यान दें कि टेलर श्रृंखला और टेलर सूत्र के बीच अंतर है: टेलर सूत्र एक सीमित योग है, अर्थात। पी -निर्धारित अंक। श्रृंखला के उस योग को याद करें एस(एक्स)
आंशिक योगों के कार्यात्मक अनुक्रम की सीमा के रूप में परिभाषित किया जा सकता है एस पी (एक्स)
कुछ अंतराल पर एक्स: इसके अनुसार, किसी फ़ंक्शन को टेलर श्रृंखला में विस्तारित करने का मतलब किसी के लिए ऐसी श्रृंखला ढूंढना है एक्सएक्स हम टेलर सूत्र को उस रूप में लिखते हैं जहाँ नोटिस जो अगर इस प्रकार, हमने साबित कर दिया है टेलर श्रृंखला में किसी फ़ंक्शन के विस्तार के लिए मानदंड।
ताकि कुछ अंतराल में कार्य हो सकेएफ(x) टेलर श्रृंखला में विस्तारित होता है, इस अंतराल पर यह आवश्यक और पर्याप्त है
तैयार किए गए मानदंड की सहायता से कोई भी प्राप्त कर सकता है पर्याप्तटेलर श्रृंखला में किसी फ़ंक्शन के विस्तार के लिए शर्तें।
मैं फ़िनबिंदु x का कुछ पड़ोस 0 किसी फ़ंक्शन के सभी डेरिवेटिव के निरपेक्ष मान समान संख्या M द्वारा सीमित होते हैं≥ 0, यानी ऊपर से यह इस प्रकार है कलन विधिकार्य विस्तार
एफ(एक्स) टेलर श्रृंखला मेंबिंदु के आसपास एक्स 0 :
1.
व्युत्पन्न फलन ढूँढना एफ(एक्स):
एफ(एक्स), एफ'(एक्स), एफ"(एक्स), एफ'"(एक्स), एफ (एन) (एक्स),… 2. हम बिंदु पर फ़ंक्शन के मान और उसके डेरिवेटिव के मान की गणना करते हैं एक्स 0 एफ(एक्स 0
), एफ'(एक्स 0
), एफ”(एक्स 0
), एफ''(x 0
), एफ (एन) (एक्स 0
),…
3. हम औपचारिक रूप से टेलर श्रृंखला लिखते हैं और परिणामी शक्ति श्रृंखला के अभिसरण का क्षेत्र ढूंढते हैं। 4. हम पर्याप्त शर्तों की पूर्ति की जाँच करते हैं, अर्थात। जिसके लिए स्थापित करें एक्सअभिसरण क्षेत्र से, शेष पद आर एन (एक्स)
पर शून्य हो जाता है इस एल्गोरिथम के अनुसार टेलर श्रृंखला में कार्यों के विस्तार को कहा जाता है परिभाषा के अनुसार टेलर श्रृंखला में किसी फ़ंक्शन का विस्तारया प्रत्यक्ष अपघटन. कार्यात्मक श्रृंखला में सबसे महत्वपूर्ण स्थान शक्ति श्रृंखला का है। किसी शक्ति शृंखला को शृंखला कहा जाता है जिसके सदस्य गैर-नकारात्मक पूर्णांक शक्तियों को बढ़ाने में व्यवस्थित शक्ति कार्य हैं एक्स, ए सी0
, सी 1
, सी 2
, सीएन
स्थिर मूल्य हैं. नंबर सी1
, सी 2
, सीएन
- श्रृंखला के सदस्यों के गुणांक, सी0
- स्वतंत्र सदस्य। घात श्रृंखला के पद संपूर्ण संख्या रेखा पर परिभाषित होते हैं। आइए अवधारणा से परिचित हों विद्युत श्रृंखला के अभिसरण का क्षेत्र।
यह परिवर्तनशील मानों का समुच्चय है एक्सजिसके लिए श्रृंखला एकत्रित होती है। पावर श्रृंखला में अभिसरण का एक काफी सरल क्षेत्र है। किसी चर के वास्तविक मानों के लिए एक्सअभिसरण क्षेत्र में या तो एक बिंदु होता है, या एक निश्चित अंतराल (अभिसरण का अंतराल) होता है, या संपूर्ण अक्ष के साथ मेल खाता है बैल
. घात श्रृंखला में प्रतिस्थापित करते समय, मान एक्स= 0 आपको एक संख्या श्रृंखला मिलती है सी0
+0+0+...+0+...
, जो एकत्रित हो जाता है। इसलिए, जब एक्स= 0 किसी भी शक्ति श्रृंखला को अभिसरण करता है और, इसलिए, इसका अभिसरण क्षेत्र
कोई खाली सेट नहीं हो सकता. सभी शक्ति श्रृंखलाओं के अभिसरण क्षेत्र की संरचना एक समान है। इसे निम्नलिखित प्रमेय का उपयोग करके स्थापित किया जा सकता है। प्रमेय 1 (हाबिल का प्रमेय). यदि शक्ति श्रृंखला किसी मूल्य पर अभिसरण करती है एक्स = एक्स 0
, जो शून्य से भिन्न है, फिर यह अभिसरण करता है, और, इसके अलावा, बिल्कुल, सभी मूल्यों के लिए |एक्स| < |एक्स 0
|
. कृपया ध्यान दें: प्रारंभिक मान "x शून्य है" और "x" का कोई भी मान, जिसकी तुलना प्रारंभिक मान से की जाती है, दोनों को मॉड्यूलो में लिया जाता है - चिह्न को ध्यान में रखे बिना। परिणाम। अगर शक्ति श्रृंखला विचलन करती है
कुछ मूल्य पर एक्स = एक्स 1
, तो यह सभी मानों के लिए भिन्न हो जाता है |एक्स| > |एक्स 1
|
. जैसा कि हमने पहले पाया, कोई भी शक्ति श्रृंखला मूल्य के लिए अभिसरण करती है एक्स= 0. ऐसी शक्ति श्रृंखलाएं हैं जो केवल के लिए अभिसरण करती हैं एक्स= 0 और अन्य मानों के लिए विचलन एक्स. इस मामले को विचार से बाहर करते हुए, हम मानते हैं कि शक्ति श्रृंखला कुछ मूल्य पर अभिसरण करती है एक्स = एक्स 0
, शून्य से भिन्न। फिर, हाबिल के प्रमेय द्वारा, यह अंतराल के सभी बिंदुओं पर अभिसरण होता है]-| एक्स0
|, |एक्स 0
|[
(अंतराल, बाएँ और दाएँ सीमाएँ x के मान हैं, जिस पर शक्ति श्रृंखला अभिसरण करती है, क्रमशः ऋण चिह्न और प्लस चिह्न के साथ ली जाती है), मूल के बारे में सममित। यदि शक्ति श्रृंखला किसी मूल्य पर विचलन करती है एक्स = एक्स 1
, फिर, हाबिल के प्रमेय के परिणाम के आधार पर, यह खंड के बाहर सभी बिंदुओं पर भी विचलन करता है [-| एक्स1
|, |एक्स 1
|]
. इसका तात्पर्य यह है कि किसी भी शक्ति श्रृंखला के लिए मूल बिंदु के संबंध में सममित एक अंतराल होता है, जिसे कहा जाता है अभिसरण अंतराल
, प्रत्येक बिंदु पर जहां श्रृंखला अभिसरित होती है, सीमाओं पर अभिसरित हो सकती है, या विचलन कर सकती है, और जरूरी नहीं कि एक साथ, लेकिन खंड के बाहर, श्रृंखला अलग हो जाती है। संख्या आरशक्ति श्रृंखला के अभिसरण की त्रिज्या कहलाती है। विशेष मामलों में शक्ति श्रृंखला अभिसरण अंतराल
एक बिंदु तक पतित हो सकता है (तब श्रृंखला केवल के लिए अभिसरण होती है एक्स= 0 और यह मान लिया गया है आर= 0) या संपूर्ण संख्या रेखा का प्रतिनिधित्व करें (तब श्रृंखला संख्या रेखा के सभी बिंदुओं पर अभिसरण होती है और यह माना जाता है)। इस प्रकार, किसी शक्ति श्रृंखला के अभिसरण के क्षेत्र की परिभाषा उसका निर्धारण करना है अभिसरण की त्रिज्या
आरऔर अभिसरण अंतराल (के लिए) की सीमाओं पर श्रृंखला के अभिसरण का अध्ययन। प्रमेय 2.यदि किसी शक्ति श्रृंखला के सभी गुणांक, एक निश्चित से शुरू होकर, गैर-शून्य हैं, तो इसके अभिसरण की त्रिज्या श्रृंखला के सामान्य निम्नलिखित सदस्यों के गुणांक के पूर्ण मूल्यों के अनुपात की सीमा के बराबर है, अर्थात। उदाहरण 1. किसी शक्ति श्रृंखला के अभिसरण का क्षेत्र ज्ञात कीजिए समाधान। यहाँ सूत्र (28) का उपयोग करके, हम इस श्रृंखला के अभिसरण की त्रिज्या पाते हैं: आइए हम अभिसरण अंतराल के अंत में श्रृंखला के अभिसरण का अध्ययन करें। उदाहरण 13 से पता चलता है कि यह श्रृंखला अभिसरण करती है एक्स= 1 और पर विचलन करता है एक्स= -1. अत: अभिसरण का क्षेत्र अर्ध-अंतराल है। उदाहरण 2. किसी शक्ति श्रृंखला के अभिसरण का क्षेत्र ज्ञात कीजिए समाधान। श्रृंखला के गुणांक सकारात्मक हैं, और आइए इस अनुपात की सीमा ज्ञात करें, अर्थात्। शक्ति श्रृंखला अभिसरण त्रिज्या: हम अंतराल के अंत में श्रृंखला के अभिसरण की जांच करते हैं। मूल्य प्रतिस्थापन एक्स= -1/5 और एक्स= इस शृंखला में 1/5 देता है: इनमें से पहली श्रृंखला अभिसरण करती है (उदाहरण 5 देखें)। लेकिन फिर, पैराग्राफ "पूर्ण अभिसरण" के प्रमेय के आधार पर, दूसरी श्रृंखला भी अभिसरण करती है, और इसके अभिसरण का क्षेत्र खंड है उदाहरण 3. किसी शक्ति श्रृंखला के अभिसरण का क्षेत्र ज्ञात कीजिए समाधान। यहाँ सूत्र (28) का उपयोग करके, हम श्रृंखला के अभिसरण की त्रिज्या पाते हैं: आइए मूल्यों के लिए श्रृंखला के अभिसरण का अध्ययन करें। उन्हें क्रमशः इस श्रृंखला में प्रतिस्थापित करने पर, हमें प्राप्त होता है दोनों श्रृंखलाएं अलग-अलग हो जाती हैं क्योंकि आवश्यक अभिसरण शर्त पूरी नहीं होती है (उनके सामान्य पद शून्य पर नहीं होते हैं)। तो, अभिसरण अंतराल के दोनों सिरों पर, यह श्रृंखला विचलन करती है, और इसके अभिसरण का क्षेत्र अंतराल है। उदाहरण 5. किसी शक्ति श्रृंखला के अभिसरण का क्षेत्र ज्ञात कीजिए समाधान। हम संबंध पाते हैं, कहां, और सूत्र (28) के अनुसार इस श्रृंखला के अभिसरण की त्रिज्या अर्थात्, श्रृंखला केवल तभी अभिसरित होती है एक्स= 0 और अन्य मानों के लिए विचलन एक्स. उदाहरण दिखाते हैं कि श्रृंखला अभिसरण अंतराल के अंत में अलग-अलग व्यवहार करती है। उदाहरण 1 में श्रृंखला अभिसरण अंतराल के एक छोर पर अभिसरण करती है और दूसरे छोर पर विसरित होती है, उदाहरण 2 में यह दोनों छोर पर अभिसरण करती है, उदाहरण 3 में यह दोनों छोर पर विसरित होती है। किसी शक्ति श्रृंखला के अभिसरण की त्रिज्या का सूत्र इस धारणा के तहत प्राप्त किया जाता है कि श्रृंखला की शर्तों के सभी गुणांक, कुछ से शुरू होकर, गैर-शून्य हैं। इसलिए, सूत्र (28) का प्रयोग केवल इन मामलों में ही स्वीकार्य है। यदि इस शर्त का उल्लंघन किया जाता है, तो शक्ति श्रृंखला के अभिसरण की त्रिज्या का उपयोग करके मांगी जानी चाहिए डी'अलेम्बर्ट का चिन्ह, या, चर में परिवर्तन करके, श्रृंखला को ऐसे रूप में परिवर्तित करके जिसमें निर्दिष्ट शर्त संतुष्ट हो। उदाहरण 6. किसी शक्ति श्रृंखला के अभिसरण का अंतराल ज्ञात कीजिए समाधान। इस श्रृंखला में विषम डिग्री वाले पद शामिल नहीं हैं एक्स. इसलिए, हम सेटिंग द्वारा श्रृंखला को बदलते हैं। तब हमें श्रृंखला प्राप्त होती है जिसकी अभिसरण त्रिज्या ज्ञात करने के लिए सूत्र (28) का उपयोग किया जा सकता है। चूँकि , और , तो इस श्रृंखला के अभिसरण की त्रिज्या समानता से हम प्राप्त करते हैं, इसलिए, यह श्रृंखला अंतराल पर अभिसरण करती है। एक शक्ति श्रृंखला के लिए चलो अभिसरण की त्रिज्या आर> 0, यानी यह श्रृंखला अंतराल पर अभिसरित होती है। फिर प्रत्येक मान एक्सअभिसरण के अंतराल से श्रृंखला का कुछ योग मेल खाता है। इसलिए, घात श्रृंखला का योग एक फलन है एक्सअभिसरण के अंतराल पर. इसके माध्यम से निरूपित करना एफ(एक्स), हम समानता लिख सकते हैं इसे इस अर्थ में समझें कि प्रत्येक बिंदु पर श्रृंखला का योग एक्सअभिसरण के अंतराल से फ़ंक्शन के मूल्य के बराबर है एफ(एक्स) इस समय। उसी अर्थ में, हम कहेंगे कि शक्ति श्रृंखला (29) फ़ंक्शन में परिवर्तित हो जाती है एफ(एक्स) अभिसरण के अंतराल पर. अभिसरण के अंतराल के बाहर, समानता (30) का कोई अर्थ नहीं है। उदाहरण 7घात श्रृंखला का योग ज्ञात कीजिए समाधान। यह एक ज्यामितीय श्रृंखला है ए= 1, और क्यू= एक्स. इसलिए, इसका योग एक फलन है केवल मानों के लिए मान्य है, यद्यपि फ़ंक्शन यह दिखाया जा सकता है कि शक्ति श्रृंखला का योग एफ(एक्स) अभिसरण के अंतराल के भीतर किसी भी खंड पर निरंतर और भिन्न है, विशेष रूप से, श्रृंखला के अभिसरण के अंतराल के किसी भी बिंदु पर। आइए हम पद-दर-पद विभेदन और शक्ति श्रृंखला के एकीकरण पर प्रमेय प्रस्तुत करें। प्रमेय 1.इसके अभिसरण के अंतराल में शक्ति श्रृंखला (30) को असीमित संख्या में पद दर पद विभेदित किया जा सकता है, और परिणामी शक्ति श्रृंखला में मूल श्रृंखला के समान अभिसरण की त्रिज्या होती है, और उनका योग क्रमशः बराबर होता है। प्रमेय 2.पावर श्रृंखला (30) को 0 से सीमा के भीतर असीमित संख्या में शब्द दर शब्द एकीकृत किया जा सकता है एक्स, यदि , और परिणामी शक्ति श्रृंखला में मूल श्रृंखला के समान अभिसरण त्रिज्या है, और उनका योग क्रमशः बराबर है कार्य करने दो एफ(एक्स), जिसे एक शक्ति श्रृंखला में विस्तारित किया जाना है, अर्थात। फॉर्म में प्रतिनिधित्व करें (30): समस्या गुणांक निर्धारित करने की है ……………………………………………….. (31) समानता (30) और (31) में मानते हुए एक्स= 0, हम पाते हैं पाए गए भावों को समानता (30) में प्रतिस्थापित करने पर, हम प्राप्त करते हैं आइए हम कुछ प्रारंभिक कार्यों के मैकलॉरिन श्रृंखला विस्तार का पता लगाएं। उदाहरण 8मैकलॉरिन श्रृंखला में फ़ंक्शन का विस्तार करें समाधान। इस फ़ंक्शन के व्युत्पन्न फ़ंक्शन के समान ही हैं: इसलिए, जब एक्स= 0 हमारे पास है इन मानों को सूत्र (32) में प्रतिस्थापित करने पर, हम वांछित विस्तार प्राप्त करते हैं: यह श्रृंखला संपूर्ण संख्या रेखा पर अभिसरण करती है (इसके अभिसरण की त्रिज्या है)।
समाधान. अपघटन (1) में हम x को -x 2 से प्रतिस्थापित करते हैं, हमें मिलता है:
, -∞
समाधान. हमारे पास है
सूत्र (4) का उपयोग करके, हम लिख सकते हैं:
सूत्र -x में x के स्थान पर प्रतिस्थापित करने पर, हमें प्राप्त होता है:
यहां से हम पाते हैं: ln(1+x)-ln(1-x) = -
कोष्ठक का विस्तार करने, श्रृंखला के पदों को पुनर्व्यवस्थित करने और समान पदों की कमी करने पर, हमें मिलता है
. यह श्रृंखला अंतराल (-1;1) में अभिसरण करती है क्योंकि यह दो श्रृंखलाओं से प्राप्त होती है, जिनमें से प्रत्येक इस अंतराल में अभिसरण करती है।
सूत्र (1)-(5) का उपयोग टेलर श्रृंखला में संबंधित कार्यों का विस्तार करने के लिए भी किया जा सकता है, अर्थात। धनात्मक पूर्णांक घातों में कार्यों के विस्तार के लिए ( हा). ऐसा करने के लिए, किसी एक फ़ंक्शन (1) - (5) को प्राप्त करने के लिए किसी दिए गए फ़ंक्शन पर ऐसे समान परिवर्तन करना आवश्यक है, जिसमें इसके बजाय एक्सलागत k( हा) m , जहां k एक स्थिर संख्या है, m एक धनात्मक पूर्णांक है। वेरिएबल को बदलना अक्सर सुविधाजनक होता है टी=हाऔर मैकलॉरिन श्रृंखला में t के संबंध में परिणामी फ़ंक्शन का विस्तार करें।
समाधान। सबसे पहले हम 1-x-6x 2 =(1-3x)(1+2x) , पाते हैं।
प्रारंभिक करने के लिए:
अभिसरण क्षेत्र के साथ |x|< 1/3.
समाधान. इस समस्या को, पहले की तरह, टेलर श्रृंखला की परिभाषा का उपयोग करके हल किया जा सकता है, जिसके लिए कार्यों के व्युत्पन्न और उनके मूल्यों को ढूंढना आवश्यक है एक्स=3. हालाँकि, मौजूदा अपघटन (5) का उपयोग करना आसान होगा:
=
परिणामी श्रृंखला या -3 पर अभिसरित होती है
समाधान.
श्रृंखला , या -2 पर एकत्रित होती है< x < 5.
समाधान. आइए प्रतिस्थापन t=x-2 करें:
विस्तार (3) का उपयोग करते हुए, जिसमें हम x के लिए π/4 t प्रतिस्थापित करते हैं, हमें मिलता है:
परिणामी श्रृंखला -∞ पर दिए गए फ़ंक्शन में परिवर्तित हो जाती है< π / 4 t<+∞, т.е. при (-∞
, (-∞पावर श्रृंखला का उपयोग करके अनुमानित गणना
अनुमानित गणनाओं में पावर श्रृंखला का व्यापक रूप से उपयोग किया जाता है। उनकी मदद से, दी गई सटीकता के साथ, आप जड़ों, त्रिकोणमितीय कार्यों, संख्याओं के लघुगणक, निश्चित अभिन्नों के मूल्यों की गणना कर सकते हैं। श्रृंखला का उपयोग विभेदक समीकरणों के एकीकरण में भी किया जाता है।
पावर श्रृंखला में फ़ंक्शन के विस्तार पर विचार करें:
किसी दिए गए बिंदु पर किसी फ़ंक्शन के अनुमानित मान की गणना करना एक्स, संकेतित श्रृंखला के अभिसरण के क्षेत्र से संबंधित, पहला एनसदस्य ( एनएक सीमित संख्या है), और शेष पद हटा दिए जाते हैं:
प्राप्त अनुमानित मान की त्रुटि का अनुमान लगाने के लिए, छोड़े गए अवशिष्ट r n (x) का अनुमान लगाना आवश्यक है। इसके लिए निम्नलिखित विधियों का उपयोग किया जाता है:
समाधान. आइए अपघटन का उपयोग करें, जहां x=1/2 (पिछले विषय में उदाहरण 5 देखें):
आइए देखें कि क्या हम विस्तार के पहले तीन पदों के बाद शेषफल को त्याग सकते हैं, इसके लिए हम अनंत रूप से घटती ज्यामितीय प्रगति के योग का उपयोग करके इसका मूल्यांकन करते हैं:
अतः हम इस शेषफल को त्याग कर प्राप्त कर सकते हैं
समाधान. आइए द्विपद श्रृंखला का उपयोग करें। चूँकि 5 3, 130 का निकटतम पूर्णांक घन है, इसलिए संख्या 130 को 130=5 3 +5 के रूप में दर्शाने की सलाह दी जाती है। 
चूँकि लीबनिज़ परीक्षण को संतुष्ट करने वाली प्राप्त संकेत-प्रत्यावर्ती श्रृंखला का चौथा पद पहले से ही आवश्यक सटीकता से कम है:
, इसलिए इसे और इसके बाद के शब्दों को ख़ारिज किया जा सकता है।
कई व्यावहारिक रूप से आवश्यक निश्चित या अनुचित अभिन्नों की गणना न्यूटन-लीबनिज सूत्र का उपयोग करके नहीं की जा सकती है, क्योंकि इसका अनुप्रयोग एक एंटीडेरिवेटिव खोजने से जुड़ा हुआ है, अक्सर प्राथमिक कार्यों में अभिव्यक्ति नहीं होती है। ऐसा भी होता है कि प्रतिअवकलन खोजना संभव है, लेकिन अनावश्यक रूप से श्रमसाध्य। हालाँकि, यदि इंटीग्रैंड को एक शक्ति श्रृंखला में विस्तारित किया जाता है, और एकीकरण सीमाएँ इस श्रृंखला के अभिसरण के अंतराल से संबंधित हैं, तो पूर्व निर्धारित सटीकता के साथ इंटीग्रल की अनुमानित गणना संभव है।
समाधान. संबंधित अनिश्चितकालीन अभिन्न अंग को प्रारंभिक कार्यों में व्यक्त नहीं किया जा सकता है, अर्थात। एक "असंभव अभिन्न" है। न्यूटन-लीबनिज फॉर्मूला यहां लागू नहीं किया जा सकता। आइए हम लगभग अभिन्न की गणना करें।
पाप के लिए श्रृंखला को पद दर पद विभाजित करना एक्सपर एक्स, हम पाते हैं: 
इस श्रृंखला को पद दर पद एकीकृत करना (यह संभव है, क्योंकि एकीकरण की सीमाएं इस श्रृंखला के अभिसरण के अंतराल से संबंधित हैं), हम प्राप्त करते हैं:
चूँकि परिणामी श्रृंखला लीबनिज़ की शर्तों को पूरा करती है और दी गई सटीकता के साथ वांछित मूल्य प्राप्त करने के लिए पहले दो शब्दों का योग लेना पर्याप्त है।
इस प्रकार, हम पाते हैं  .
.
समाधान.

![]() . आइए देखें कि क्या हम परिणामी श्रृंखला के दूसरे पद के बाद शेषफल को हटा सकते हैं।
. आइए देखें कि क्या हम परिणामी श्रृंखला के दूसरे पद के बाद शेषफल को हटा सकते हैं।
0.0001<0.001. Следовательно,  .
. ,
वे।
,
वे। =
..
=
..
 किसी भी क्रम का व्युत्पन्न है। क्या इसे पावर श्रृंखला में विस्तारित किया जा सकता है, यदि हां, तो इस श्रृंखला को कैसे खोजें? समस्या का दूसरा भाग हल करना आसान है, तो चलिए इससे शुरू करते हैं।
किसी भी क्रम का व्युत्पन्न है। क्या इसे पावर श्रृंखला में विस्तारित किया जा सकता है, यदि हां, तो इस श्रृंखला को कैसे खोजें? समस्या का दूसरा भाग हल करना आसान है, तो चलिए इससे शुरू करते हैं। इसे एक बिंदु वाले अंतराल में अभिसरण करने वाली शक्ति श्रृंखला के योग के रूप में दर्शाया जा सकता है एक्स 0 :
इसे एक बिंदु वाले अंतराल में अभिसरण करने वाली शक्ति श्रृंखला के योग के रूप में दर्शाया जा सकता है एक्स 0 :
 =
..
(*)
=
..
(*) .
. =
..
=
..
 .
. =
..
=
..
 , कहाँ
, कहाँ  .
. , कहाँ
, कहाँ
 ,
,
 ,
,
 ,
…,
,
…,
 ,….,
,…., .
.
3.2. टेलर श्रृंखला में किसी फ़ंक्शन के विस्तार के लिए पर्याप्त स्थितियाँ
 बिंदु x के किसी पड़ोस में 0 तक डेरिवेटिव हैं (एन+
1)-वें क्रम को सम्मिलित करते हुए, इस पड़ोस में हमारे पास हैFORMULA
टेलर
बिंदु x के किसी पड़ोस में 0 तक डेरिवेटिव हैं (एन+
1)-वें क्रम को सम्मिलित करते हुए, इस पड़ोस में हमारे पास हैFORMULA
टेलर

 .
.
 हमें मिलने वाली त्रुटि को परिभाषित करता है, फ़ंक्शन को प्रतिस्थापित करता है एफ(एक्स)
बहुपद एस एन (एक्स).
हमें मिलने वाली त्रुटि को परिभाषित करता है, फ़ंक्शन को प्रतिस्थापित करता है एफ(एक्स)
बहुपद एस एन (एक्स).
 , वह
, वह  ,वे। यह फ़ंक्शन टेलर श्रृंखला में विस्तारित होता है। इसके विपरीत, यदि
,वे। यह फ़ंक्शन टेलर श्रृंखला में विस्तारित होता है। इसके विपरीत, यदि  , वह
, वह  .
. , कहाँआर एन (एक्स) टेलर श्रृंखला का शेष भाग है।
, कहाँआर एन (एक्स) टेलर श्रृंखला का शेष भाग है। , टीo इस पड़ोस में, फ़ंक्शन टेलर श्रृंखला में विस्तारित होता है।
, टीo इस पड़ोस में, फ़ंक्शन टेलर श्रृंखला में विस्तारित होता है। या
या
 .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]() :
:![]()
![]() ,
,![]()
![]()
![]()
पावर श्रृंखला योग. शक्ति श्रृंखला का विभेदन और एकीकरण
![]()
![]() . श्रृंखला यदि अभिसरण करती है, और इसका अभिसरण अंतराल है। अत: समानता
. श्रृंखला यदि अभिसरण करती है, और इसका अभिसरण अंतराल है। अत: समानता![]()
![]() सभी मानों के लिए परिभाषित एक्स, के अलावा एक्स= 1.
सभी मानों के लिए परिभाषित एक्स, के अलावा एक्स= 1.
पावर श्रृंखला में कार्यों का विस्तार
![]() पंक्ति (30). ऐसा करने के लिए, समानता (30) को पद दर पद विभेदित करते हुए, हम क्रमिक रूप से पाते हैं:
पंक्ति (30). ऐसा करने के लिए, समानता (30) को पद दर पद विभेदित करते हुए, हम क्रमिक रूप से पाते हैं:![]()
![]()

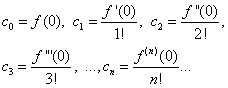
 (32)
(32)
![]() (33)
(33)

