Rozšírenie cos v Taylorovom rade. Rozšírenie funkcií do mocninových radov
16.1. Rozšírenie elementárnych funkcií v Taylorovom rade a
Maclaurin
Ukážme, že ak je na množine definovaná ľubovoľná funkcia  , v blízkosti bodu
, v blízkosti bodu  má veľa derivátov a je súčtom mocninového radu:
má veľa derivátov a je súčtom mocninového radu:
potom môžete nájsť koeficienty tohto radu.
Dosadíme v mocninnom rade  . Potom
. Potom  .
.
Nájdite prvú deriváciu funkcie  :
:
O  :
: .
.
Pre druhú deriváciu dostaneme:
O  :
: .
.
Pokračovanie v tomto postupe n akonáhle dostaneme:  .
.
Takto sme dostali mocninný rad v tvare:


 ,
,
ktorá sa volá vedľa Taylora pre funkciu  v blízkosti bodu
v blízkosti bodu  .
.
Špeciálnym prípadom Taylorovho radu je Séria Maclaurin pri  :
:



Zvyšok série Taylor (Maclaurin) sa získa vyradením hlavnej série n prvými členmi a označuje sa ako  . Potom funkcia
. Potom funkcia  možno zapísať ako súčet n prví členovia série
možno zapísať ako súčet n prví členovia série  a zvyšok
a zvyšok  :,
:,
 .
.
Zvyšok je zvyčajne  vyjadrené v rôznych vzorcoch.
vyjadrené v rôznych vzorcoch.
Jeden z nich je vo forme Lagrange:
 , Kde
, Kde  .
. .
.
Všimnite si, že v praxi sa častejšie používa séria Maclaurin. Aby bolo možné napísať funkciu  vo forme súčtu mocninových radov je potrebné:
vo forme súčtu mocninových radov je potrebné:
1) nájdite koeficienty série Maclaurin (Taylor);
2) nájdite oblasť konvergencie výsledného mocninového radu;
3) dokážte, že tento rad konverguje k funkcii  .
.
Veta1
(nevyhnutná a postačujúca podmienka pre konvergenciu Maclaurinovho radu). Nech je polomer konvergencie radu  . Aby tento rad v intervale konvergoval
. Aby tento rad v intervale konvergoval  k funkcii
k funkcii  , na splnenie podmienky je potrebné a postačujúce:
, na splnenie podmienky je potrebné a postačujúce:  v určenom intervale.
v určenom intervale.
Veta 2. Ak derivácie ľubovoľného rádu funkcie  v nejakom intervale
v nejakom intervale  v absolútnej hodnote obmedzené na rovnaký počet M, teda
v absolútnej hodnote obmedzené na rovnaký počet M, teda  , potom v tomto intervale funkcia
, potom v tomto intervale funkcia  možno rozšíriť do série Maclaurin.
možno rozšíriť do série Maclaurin.
Príklad1
.
Expandujte v Taylorovom rade okolo bodu  funkciu.
funkciu.
Riešenie.
 .
.
 ,;
,;
 ,
, ;
;
 ,
, ;
;
 ,
,
.......................................................................................................................................
 ,
, ;
;
Konvergenčný región  .
.
Príklad2
.
Rozbaľte funkciu  v Taylorovom rade okolo bodu
v Taylorovom rade okolo bodu  .
.
Riešenie:
Nájdite hodnotu funkcie a jej derivácií na  .
.
 ,
, ;
;
 ,
, ;
;
...........……………………………
 ,
, .
.
Dajme tieto hodnoty do radu. Dostaneme:
alebo  .
.
Nájdite oblasť konvergencie tohto radu. Podľa d'Alembertovho testu séria konverguje, ak
 .
.
Preto pre akékoľvek  táto hranica je menšia ako 1, a preto rozsah konvergencie radu bude:
táto hranica je menšia ako 1, a preto rozsah konvergencie radu bude:  .
.
Uvažujme niekoľko príkladov rozšírenia základných elementárnych funkcií Maclaurinovým radom. Pripomeňme, že séria Maclaurin:


 .
.
konverguje na intervale  k funkcii
k funkcii  .
.
Všimnite si, že na rozšírenie funkcie do série je potrebné:
a) nájdite koeficienty Maclaurinovho radu pre túto funkciu;
b) vypočítajte polomer konvergencie pre výsledný rad;
c) dokážte, že výsledný rad konverguje k funkcii  .
.
Príklad 3 Zvážte funkciu  .
.
Riešenie.
Vypočítajme hodnotu funkcie a jej derivácií at  .
.
Potom majú číselné koeficienty radu tvar:
pre hocikoho n. Dosaďte nájdené koeficienty do Maclaurinovho radu a získame: 
Nájdite polomer konvergencie výsledného radu, a to:
 .
.
Preto rad konverguje k intervalu  .
.
Tento rad konverguje k funkcii  pre akékoľvek hodnoty
pre akékoľvek hodnoty  , pretože na akomkoľvek intervale
, pretože na akomkoľvek intervale  funkciu
funkciu  a jeho deriváty absolútnej hodnoty sú obmedzené počtom
a jeho deriváty absolútnej hodnoty sú obmedzené počtom  .
.
Príklad4
.
Zvážte funkciu  .
.
Riešenie.
 :
:

Je ľahké vidieť, že deriváty párneho poriadku  a deriváty sú nepárneho poradia. Dosadíme nájdené koeficienty do Maclaurinovho radu a získame rozšírenie:
a deriváty sú nepárneho poradia. Dosadíme nájdené koeficienty do Maclaurinovho radu a získame rozšírenie:
Nájdite interval konvergencie tohto radu. Podľa d'Alembertovho znamenia:
pre hocikoho  . Preto rad konverguje k intervalu
. Preto rad konverguje k intervalu  .
.
Tento rad konverguje k funkcii  , pretože všetky jeho deriváty sú obmedzené na jednotu.
, pretože všetky jeho deriváty sú obmedzené na jednotu.
Príklad5
.
 .
.
Riešenie.
Nájdite hodnotu funkcie a jej derivácií na  :
:

Takže koeficienty tohto radu:  A
A  , teda:
, teda:
Podobne ako v predchádzajúcom riadku, oblasť konvergencie  . Rad konverguje k funkcii
. Rad konverguje k funkcii  , pretože všetky jeho deriváty sú obmedzené na jednotu.
, pretože všetky jeho deriváty sú obmedzené na jednotu.
Upozorňujeme, že funkcia  nepárne a radové rozšírenie v nepárnych mocninách, funkcia
nepárne a radové rozšírenie v nepárnych mocninách, funkcia  – párne a rozšírenie do radu v párnych mocninách.
– párne a rozšírenie do radu v párnych mocninách.
Príklad6
.
Binomický rad:  .
.
Riešenie.
Nájdite hodnotu funkcie a jej derivácií na  :
:

Z toho je vidieť, že:

Dosaďte tieto hodnoty koeficientov do Maclaurinovho radu a získajme rozšírenie tejto funkcie do mocninového radu:
Nájdite polomer konvergencie tohto radu:

Preto rad konverguje k intervalu  . V hraničných bodoch pri
. V hraničných bodoch pri  A
A  rad môže alebo nemusí konvergovať v závislosti od exponentu
rad môže alebo nemusí konvergovať v závislosti od exponentu  .
.
Študovaný rad konverguje na intervale  k funkcii
k funkcii  , teda súčet série
, teda súčet série  pri
pri  .
.
Príklad7
.
Rozšírme funkciu v sérii Maclaurin  .
.
Riešenie.
Na rozšírenie tejto funkcie na rad používame binomický rad at  . Dostaneme:
. Dostaneme: 
Na základe vlastnosti mocninného radu (mocninový rad možno integrovať v oblasti jeho konvergencie) nájdeme integrál ľavej a pravej strany tohto radu:
Nájdite oblasť konvergencie tohto radu:  ,
,
to znamená, že oblasťou konvergencie tohto radu je interval  . Určme konvergenciu radu na koncoch intervalu. O
. Určme konvergenciu radu na koncoch intervalu. O 
 . Táto séria je harmonická séria, to znamená, že sa rozchádza. O
. Táto séria je harmonická séria, to znamená, že sa rozchádza. O  dostaneme číselný rad so spoločným členom
dostaneme číselný rad so spoločným členom  .
.
Séria konverguje podľa Leibnizovho kritéria. Oblasťou konvergencie tohto radu je teda interval  .
.
16.2. Aplikácia mocninových radov v približných výpočtoch
V približných výpočtoch zohrávajú mocninné rady mimoriadne dôležitú úlohu. S ich pomocou boli zostavené tabuľky goniometrických funkcií, tabuľky logaritmov, tabuľky hodnôt iných funkcií, ktoré sa používajú v rôznych oblastiach vedomostí, napríklad v teórii pravdepodobnosti a matematickej štatistike. Okrem toho je rozšírenie funkcií do mocninového radu užitočné pre ich teoretické štúdium. Hlavným problémom pri používaní mocninových radov v približných výpočtoch je otázka odhadu chyby pri nahradení súčtu radu súčtom jeho prvého nčlenov.
Zoberme si dva prípady:
funkcia je rozšírená do radu so striedaním znamienok;
funkcia je rozšírená do radu konštantných znamienkov.
Výpočet pomocou striedavých radov
Nechajte funkciu  rozšírené do striedavého výkonového radu. Potom pri výpočte tejto funkcie pre konkrétnu hodnotu
rozšírené do striedavého výkonového radu. Potom pri výpočte tejto funkcie pre konkrétnu hodnotu  dostaneme číselný rad, na ktorý môžeme aplikovať Leibnizovo kritérium. V súlade s týmto kritériom, ak sa súčet série nahradí súčtom jej prvého nčleny, potom absolútna chyba nepresiahne prvý člen zvyšku tohto radu, to znamená:
dostaneme číselný rad, na ktorý môžeme aplikovať Leibnizovo kritérium. V súlade s týmto kritériom, ak sa súčet série nahradí súčtom jej prvého nčleny, potom absolútna chyba nepresiahne prvý člen zvyšku tohto radu, to znamená:  .
.
Príklad8
.
Vypočítajte  s presnosťou 0,0001.
s presnosťou 0,0001.
Riešenie.
Na to použijeme sériu Maclaurin  , nahradením hodnoty uhla v radiánoch:
, nahradením hodnoty uhla v radiánoch:

Ak porovnáme prvý a druhý člen radu s danou presnosťou, potom: .
Tretí termín rozšírenia:
menšia ako špecifikovaná presnosť výpočtu. Preto počítať  stačí nechať dva termíny série, tzn
stačí nechať dva termíny série, tzn
 .
.
Teda  .
.
Príklad9
.
Vypočítajte  s presnosťou 0,001.
s presnosťou 0,001.
Riešenie.
Použijeme vzorec binomického radu. Aby sme to urobili, napíšme  ako:
ako:  .
.
V tomto výraze  ,
,

Porovnajme každý z výrazov série s presnosťou, ktorá je špecifikovaná. To je jasné  . Preto počítať
. Preto počítať  stačí nechať tri termíny série.
stačí nechať tri termíny série.
 alebo
alebo  .
.
Výpočet pomocou kladných sérií
Príklad10
.
Vypočítajte číslo  s presnosťou 0,001.
s presnosťou 0,001.
Riešenie.
V rade pre funkciu  poďme nahradiť
poďme nahradiť  . Dostaneme:
. Dostaneme:

Odhadnime chybu, ktorá vznikne pri nahradení súčtu radu súčtom prvého  členov. Zapíšme si zjavnú nerovnosť:
členov. Zapíšme si zjavnú nerovnosť:
to je 2< <3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
<3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
 ,
, .
.
Podľa problému musíte nájsť n tak, že platí nasledujúca nerovnosť:  alebo
alebo  .
.
Je ľahké skontrolovať, že kedy n= 6: .
.
teda  .
.
Príklad11
.
Vypočítajte  s presnosťou 0,0001.
s presnosťou 0,0001.
Riešenie.
Všimnite si, že na výpočet logaritmov je možné použiť sériu funkcie  , ale tento rad konverguje veľmi pomaly a na dosiahnutie danej presnosti by bolo potrebné odobrať 9999 členov! Preto sa na výpočet logaritmov spravidla používa rad funkcie
, ale tento rad konverguje veľmi pomaly a na dosiahnutie danej presnosti by bolo potrebné odobrať 9999 členov! Preto sa na výpočet logaritmov spravidla používa rad funkcie  , ktorá konverguje na intervale
, ktorá konverguje na intervale  .
.
Poďme počítať  pomocou tejto série. Nechaj
pomocou tejto série. Nechaj  , Potom
, Potom  .
.
teda  ,
,
Aby bolo možné vypočítať  s danou presnosťou vezmite súčet prvých štyroch výrazov:
s danou presnosťou vezmite súčet prvých štyroch výrazov:  .
.
Zvyšok série  zahoďme to. Odhadnime chybu. To je zrejmé
zahoďme to. Odhadnime chybu. To je zrejmé 
alebo  .
.

V rade, ktorý bol použitý na výpočet, teda stačilo vziať len prvé štyri členy namiesto 9999 v rade pre funkciu  .
.
Samodiagnostické otázky
1. Čo je to Taylorov rad?
2. Akú podobu mala séria Maclaurin?
3. Formulujte vetu o expanzii funkcie v Taylorovom rade.
4. Napíšte rozšírenie Maclaurinovho radu hlavných funkcií.
5. Označte oblasti konvergencie uvažovaného radu.
6. Ako odhadnúť chybu pri približných výpočtoch pomocou mocninových radov?
Ak má funkcia f(x) derivácie všetkých rádov na určitom intervale obsahujúcom bod a, možno na ňu použiť Taylorov vzorec:
,
Kde r n– takzvaný zvyšok alebo zvyšok radu, možno ho odhadnúť pomocou Lagrangeovho vzorca:
, kde číslo x je medzi x a a.
Pravidlá pre zadávanie funkcií:
Ak pre nejakú hodnotu X r n→0 o hod n→∞, potom v limite sa Taylorov vzorec stane konvergentným pre túto hodnotu Taylorova séria:
,
Funkciu f(x) je teda možné rozšíriť na Taylorov rad v uvažovanom bode x, ak:
1) má deriváty všetkých rádov;
2) zostrojený rad v tomto bode konverguje.
Keď a = 0 dostaneme rad tzv neďaleko Maclaurinu:
,
Rozšírenie najjednoduchších (elementárnych) funkcií v rade Maclaurin:
Exponenciálne funkcie
R = ∞
Goniometrické funkcie ![]() R = ∞
R = ∞ ![]() R = ∞
R = ∞
, (-π/2< x < π/2), R=π/2
Funkcia actgx sa nerozpína v mocninách x, pretože ctg0=∞
Hyperbolické funkcie
Logaritmické funkcie
, -1
Binomický rad
![]() .
.
Príklad č.1. Rozbaľte funkciu na mocninový rad f(x)= 2X.
Riešenie. Nájdeme hodnoty funkcie a jej derivátov na X=0
f(x) = 2X, f( 0)
= 2 0
=1;
f"(x) = 2X ln2, f"( 0)
= 2 0
ln2= ln2;
f""(x) = 2X V 22, f""( 0)
= 2 0
ln 2 2 = ln 2 2;
…
f(n)(x) = 2X ln n 2, f(n)( 0)
= 2 0
ln n 2 = ln n 2.
Nahradením získaných hodnôt derivátov do vzorca Taylorovho radu získame:
Polomer konvergencie tohto radu sa rovná nekonečnu, preto toto rozšírenie platí pre -∞<X<+∞.
Príklad č.2. Napíšte Taylorovu sériu v mocninách ( X+4) pre funkciu f(x)= e X.
Riešenie. Hľadanie derivácií funkcie e X a ich hodnoty v bode X=-4.
f(x)= e X, f(-4)
= e -4
;
f"(x)= e X, f"(-4)
= e -4
;
f""(x)= e X, f""(-4)
= e -4
;
…
f(n)(x)= e X, f(n)( -4)
= e -4
.
Preto požadovaný Taylorov rad funkcie má tvar:
Toto rozšírenie platí aj pre -∞<X<+∞.
Príklad č.3. Rozbaľte funkciu f(x)=ln X v sérii v mocnostiach ( X- 1),
(t. j. v Taylorovom rade v blízkosti bodu X=1).
Riešenie. Nájdite deriváty tejto funkcie.
f(x)=lnx , , , ,
f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f (n) =(- 1) n-1 (n-1)!
Nahradením týchto hodnôt do vzorca získame požadovaný Taylorov rad:
Pomocou d'Alembertovho testu môžete overiť, že séria konverguje pri ½x-1½<1 . Действительно,
Rad konverguje, ak ½ X- 1½<1, т.е. при 0<X<2. При X=2 dostaneme striedavý rad, ktorý spĺňa podmienky Leibnizovho kritéria. Keď x=0 funkcia nie je definovaná. Oblasť konvergencie Taylorovho radu je teda polootvorený interval (0;2].
Príklad č.4. Rozbaľte funkciu na mocninový rad. Príklad č.5. Rozšírte funkciu do série Maclaurin. Komentujte
.
Táto metóda je založená na teoréme o jedinečnosti expanzie funkcie v mocninnom rade. Podstatou tejto vety je, že v okolí toho istého bodu nemožno získať dva rôzne mocninné rady, ktoré by konvergovali k tej istej funkcii, bez ohľadu na to, ako sa jej expanzia vykonáva. Príklad č. 5a. Rozšírte funkciu v Maclaurinovom rade a označte oblasť konvergencie. Zlomok 3/(1-3x) možno považovať za súčet nekonečne klesajúcej geometrickej postupnosti s menovateľom 3x, ak |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
Príklad č.6. Rozviňte funkciu do Taylorovho radu v blízkosti bodu x = 3. Príklad č. 7. Napíšte Taylorov rad v mocninách (x -1) funkcie ln(x+2) . Príklad č. 8. Rozviňte funkciu f(x)=sin(πx/4) do Taylorovho radu v blízkosti bodu x =2. Príklad č.1. Vypočítajte ln(3) s presnosťou na 0,01. Príklad č.2. Vypočítajte s presnosťou na 0,0001. Príklad č.3. Vypočítajte integrál ∫ 0 1 4 sin (x) x s presnosťou 10 -5 . Príklad č.4. Vypočítajte integrál ∫ 0 1 4 e x 2 s presnosťou na 0,001. Rozšírenie funkcie do sérií Taylor, Maclaurin a Laurent na mieste na trénovanie praktických zručností. Táto sériová expanzia funkcie umožňuje matematikom odhadnúť približnú hodnotu funkcie v určitom bode jej definície. Je oveľa jednoduchšie vypočítať takúto funkčnú hodnotu v porovnaní s použitím Bredisovej tabuľky, ktorá je v dobe počítačovej techniky taká irelevantná. Rozšíriť funkciu do Taylorovho radu znamená vypočítať koeficienty lineárnych funkcií tohto radu a zapísať ho v správnom tvare. Študenti si zamieňajú tieto dve série, pričom nechápu, čo je všeobecný prípad a čo špeciálny prípad druhého. Pripomeňme raz a navždy, že Maclaurinov rad je špeciálny prípad Taylorovho radu, teda ide o Taylorov rad, ale v bode x = 0. Všetky stručné heslá na rozšírenie známych funkcií, ako e^x, Sin(x), Cos(x) a iné, toto sú expanzie Taylorovho radu, ale v bode 0 pre argument. Pre funkcie komplexného argumentu je Laurentov rad najbežnejším problémom v TFCT, pretože predstavuje obojstranný nekonečný rad. Je to súčet dvoch sérií. Odporúčame vám pozrieť si príklad rozkladu priamo na webovej stránke; je to veľmi jednoduché kliknutím na „Príklad“ s ľubovoľným číslom a potom na tlačidlo „Riešenie“. Je to práve toto rozšírenie funkcie do radu, ktoré je spojené s majorizačným radom, ktorý obmedzuje pôvodnú funkciu v určitej oblasti pozdĺž osi y, ak premenná patrí do oblasti x x. Vektorová analýza sa porovnáva s ďalšou zaujímavou disciplínou v matematike. Keďže každý výraz je potrebné preskúmať, proces si vyžaduje pomerne veľa času. Akákoľvek Taylorova séria môže byť spojená s Maclaurinovou sériou nahradením x0 nulou, ale pre Maclaurinovu sériu niekedy nie je zrejmé reprezentovať Taylorovu sériu naopak. Ako keby to nebolo potrebné robiť v čistej forme, je to zaujímavé pre všeobecný sebarozvoj. Každý Laurentov rad zodpovedá obojstrannému nekonečnému mocninnému radu v celočíselných mocninách z-a, inými slovami, radom rovnakého Taylorovho typu, ale mierne odlišných vo výpočte koeficientov. O oblasti konvergencie Laurentovho radu budeme hovoriť o niečo neskôr, po niekoľkých teoretických výpočtoch. Ako v minulom storočí, postupné rozširovanie funkcie do radu sa dá len ťažko dosiahnuť jednoduchým privedením členov k spoločnému menovateľovi, pretože funkcie v menovateľoch sú nelineárne. Pri formulácii úloh je potrebný približný výpočet funkčnej hodnoty. Zamyslite sa nad skutočnosťou, že keď je argumentom Taylorovho radu lineárna premenná, expanzia nastáva v niekoľkých krokoch, ale obraz je úplne iný, keď argumentom expandovanej funkcie je komplexná alebo nelineárna funkcia, potom proces reprezentovanie takejto funkcie v mocninnom rade je zrejmé, pretože týmto spôsobom je teda ľahké vypočítať, aj keď približnú hodnotu, v akomkoľvek bode v oblasti definície, s minimálnou chybou, ktorá má malý vplyv na ďalšie výpočty. To platí aj pre sériu Maclaurin. keď je potrebné vypočítať funkciu v nulovom bode. Samotnú sériu Laurent tu však zastupuje rozšírenie na rovinu s pomyselnými jednotkami. Nie bez úspechu bude tiež správne riešenie problému v priebehu celkového procesu. V matematike tento prístup nie je známy, ale objektívne existuje. Výsledkom je, že môžete dospieť k záveru o takzvaných bodových podmnožinách a pri rozširovaní funkcie v rade musíte použiť metódy známe pre tento proces, ako je napríklad aplikácia teórie derivácií. Opäť sme sa presvedčili, že pravdu mal učiteľ, ktorý vyslovil svoje predpoklady o výsledkoch post-výpočtových výpočtov. Všimnime si, že Taylorova séria, získaná podľa všetkých kánonov matematiky, existuje a je definovaná na celej číselnej osi, avšak, milí používatelia webovej služby, nezabudnite na typ pôvodnej funkcie, pretože sa môže ukázať že spočiatku je potrebné stanoviť definičný obor funkcie, teda napísať a vylúčiť z ďalšieho uvažovania tie body, v ktorých funkcia nie je definovaná v obore reálnych čísel. Dá sa povedať, že to ukáže vašu rýchlosť pri riešení problému. Konštrukcia série Maclaurin s nulovou hodnotou argumentu nebude výnimkou z toho, čo bolo povedané. Proces hľadania domény definície funkcie nebol zrušený a k tejto matematickej operácii musíte pristupovať so všetkou vážnosťou. V prípade Laurentovho radu, ktorý obsahuje hlavnú časť, sa parameter „a“ bude nazývať izolovaný singulárny bod a Laurentov rad sa rozšíri do prstenca – ide o priesečník oblastí konvergencie jeho častí, teda bude nasledovať zodpovedajúca veta. Nie všetko je ale také zložité, ako by sa na prvý pohľad neskúsenému študentovi mohlo zdať. Po preštudovaní Taylorovej série môžete ľahko pochopiť Laurentovu sériu - zovšeobecnený prípad rozšírenia priestoru čísel. Akákoľvek sériová expanzia funkcie môže byť vykonaná iba v bode v oblasti definície funkcie. Mali by sa brať do úvahy vlastnosti funkcií, ako je periodicita alebo nekonečná diferencovateľnosť. Odporúčame tiež použiť tabuľku hotových rozšírení elementárnych funkcií Taylorovho radu, keďže jedna funkcia môže byť reprezentovaná až desiatkami rôznych mocninových radov, ako je zrejmé z našej online kalkulačky. Online sériu Maclaurin je ľahké určiť, ak využívate jedinečnú webovú službu, stačí zadať správnu písomnú funkciu a prezentovanú odpoveď dostanete v priebehu niekoľkých sekúnd, zaručene bude presná a v štandardná písomná forma. Výsledok môžete skopírovať priamo do čistej kópie na odovzdanie učiteľovi. Bolo by správne najprv určiť analytickosť príslušnej funkcie v kruhoch a potom jednoznačne uviesť, že je rozšíriteľná v Laurentovom rade vo všetkých takýchto kruhoch. Je dôležité nestratiť zo zreteľa podmienky Laurentovej série obsahujúcej negatívne sily. Zamerajte sa na to čo najviac. Dobre využite Laurentovu vetu o expanzii funkcie v celočíselných mocninách. V teórii funkčných radov ústredné miesto zaujíma časť venovaná expanzii funkcie do radu. Nastáva teda problém: pre danú funkciu
je potrebné nájsť takýto mocninný rad ktorý konvergoval na určitom intervale a jeho súčet sa rovnal Táto úloha sa nazýva problém rozšírenia funkcie do mocninového radu. Nevyhnutná podmienka rozložiteľnosti funkcie v mocninnom rade je jeho diferencovateľnosť nekonečne veľakrát – to vyplýva z vlastností konvergentných mocninných radov. Táto podmienka je spravidla splnená pre elementárne funkcie v oblasti ich definície. Predpokladajme teda, že funkcia Predpokladajme, že funkcia Kde A 0 ,A 1 ,A 2 ,...,A P ,...
– neznáme (zatiaľ) koeficienty. Dajme rovnosť (*) hodnotu x = x 0 ,
potom dostaneme Rozlišujme mocninný rad (*) člen po člene a veriť tu x = x 0 ,
dostaneme Ďalším diferenciáciou získame rad veriaceho x = x 0 ,
dostaneme Po P- dostávame viacnásobnú diferenciáciu Za predpokladu poslednej rovnosti x = x 0 ,
dostaneme Takže koeficienty sú nájdené dosadením ktorých do radu (*) dostaneme Výsledný rad je tzv vedľa Taylora
pre funkciu
Tak sme to zistili ak je možné funkciu rozšíriť na mocninný rad (x - x 0 ), potom je toto rozšírenie jedinečné a výsledný rad je nevyhnutne Taylorovým radom. Všimnite si, že Taylorov rad možno získať pre akúkoľvek funkciu, ktorá má v bode derivácie akéhokoľvek rádu x = x 0 .
To ale neznamená, že medzi funkciu a výsledný rad možno umiestniť znamienko rovnosti, t.j. že súčet radu sa rovná pôvodnej funkcii. Po prvé, takáto rovnosť môže mať zmysel len v oblasti konvergencie a Taylorov rad získaný pre funkciu môže divergovať a po druhé, ak Taylorov rad konverguje, potom sa jeho súčet nemusí zhodovať s pôvodnou funkciou. Sformulujme vyhlásenie, pomocou ktorého bude úloha vyriešená. Ak funkcia
KdeR n (X)-zvyšný člen Taylorovho vzorca – má tvar (Lagrangeova forma) Kde
bodkaξ
leží medzi x a x 0 . Všimnite si, že medzi Taylorovým radom a Taylorovým vzorcom je rozdiel: Taylorov vzorec je konečný súčet, t.j. P - pevné číslo. Pripomeňme, že súčet série S(X)
možno definovať ako hranicu funkčnej postupnosti čiastkových súčtov S P (X)
v nejakom intervale X: Podľa toho expandovať funkciu do Taylorovho radu znamená nájsť taký rad, že pre ľubovoľný XX Napíšme Taylorov vzorec v tvare kde Všimni si Ak Tak sme dokázali kritérium rozložiteľnosti funkcie v Taylorovom rade.
Aby bola funkciaf(x) expanduje do Taylorovho radu, je potrebné a postačujúce, aby na tomto intervale
Pomocou formulovaného kritéria je možné získať dostatočnépodmienky rozložiteľnosti funkcie v Taylorovom rade.
Ak vnejaké okolie bodu x 0 absolútne hodnoty všetkých derivácií funkcie sú obmedzené na rovnaké číslo M≥ 0, t.j. Z vyššie uvedeného vyplýva algoritmurozšírenie funkcie
f(X) v sérii Taylor v blízkosti bodu X 0 :
1.
Hľadanie derivácií funkcií f(X):
f(x), f’(x), f”(x), f’”(x), f (n) (X),… 2. Vypočítajte hodnotu funkcie a hodnoty jej derivácií v bode X 0 f(x 0
), f'(x 0
), f“(x 0
), f'“ (x 0
), f (n) (X 0
),…
3. Formálne napíšeme Taylorov rad a nájdeme oblasť konvergencie výsledného mocninného radu. 4. Kontrolujeme splnenie dostatočných podmienok, t.j. stanovujeme pre ktoré X z konvergenčného regiónu, zvyšok obdobia R n (X)
inklinuje k nule ako Rozšírenie funkcií do Taylorovho radu pomocou tohto algoritmu sa nazýva rozšírenie funkcie do Taylorovho radu podľa definície alebo priamy rozklad. Medzi funkčnými radmi zaujímajú najdôležitejšie miesto mocninné rady. Mocninná séria je séria ktorých členy sú mocninné funkcie usporiadané v rastúcich nezáporných celých mocninách X, A c0
, c 1
, c 2
, c n
- konštantné hodnoty. čísla c1
, c 2
, c n
- koeficienty sériových členov, c0
- voľný člen. Členy mocninového radu sú definované na celej číselnej osi. Zoznámime sa s konceptom oblasti konvergencie mocninových radov.
Ide o súbor premenných hodnôt X, pre ktoré rad konverguje. Mocninné rady majú pomerne jednoduchú oblasť konvergencie. Pre reálne premenné hodnoty X oblasť konvergencie pozostáva buď z jedného bodu, alebo je určitým intervalom (interval konvergencie), alebo sa zhoduje s celou osou Vôl
. Pri dosadzovaní hodnôt do mocninového radu X= 0 bude mať za následok číselný rad c0
+0+0+...+0+...
, ktorá konverguje. Preto, kedy X= 0 každý mocninový rad konverguje, a preto oblasť jeho konvergencie
nemôže byť prázdna množina. Štruktúra oblasti konvergencie všetkých mocninných radov je rovnaká. Dá sa určiť pomocou nasledujúcej vety. Veta 1 (Abelova veta). Ak mocninný rad konverguje na nejakej hodnote X = X 0
, odlišný od nuly, potom konverguje, a navyše absolútne, pre všetky hodnoty |X| < |X 0
|
. Poznámka: Počiatočná hodnota „X je nula“ aj akákoľvek hodnota „X“, ktorá sa porovnáva s počiatočnou hodnotou, sa berú modulo – bez zohľadnenia znamienka. Dôsledok. Ak mocninné rady sa rozchádzajú
v nejakej hodnote X = X 1
, potom sa líši pre všetky hodnoty |X| > |X 1
|
. Ako sme už skôr zistili, akýkoľvek mocninový rad konverguje k hodnote X= 0. Existujú mocninné rady, ktoré konvergujú len vtedy, keď X= 0 a rozchádzajú sa pre ostatné hodnoty X. Ak tento prípad vylúčime z úvahy, predpokladáme, že mocninný rad konverguje na nejakej hodnote X = X 0
, odlišný od nuly. Potom podľa Abelovej vety konverguje vo všetkých bodoch intervalu ]-| X0
|, |X 0
|[
(interval, ktorého ľavá a pravá hranica sú hodnoty x, v ktorých mocninný rad konverguje, braný so znamienkom mínus a znamienko plus), symetrické vzhľadom na pôvod. Ak sa mocninný rad pri určitej hodnote rozchádza X = X 1
, potom na základe následku Abelovej vety diverguje vo všetkých bodoch mimo segmentu [-| X1
|, |X 1
|]
. Z toho vyplýva, že pre každý mocninný rad existuje interval symetrický vzhľadom na počiatok, tzv interval konvergencie
, v každom bode, v ktorom rad konverguje, na hraniciach môže konvergovať, alebo sa môže divergovať, a to nemusí byť nevyhnutne súčasne, a mimo segmentu rad diverguje. číslo R sa nazýva polomer konvergencie mocninového radu. V špeciálnych prípadoch interval konvergencie mocninových radov
môže degenerovať do bodu (potom séria konverguje len vtedy, keď X= 0 a predpokladá sa, že R= 0) alebo predstavujú celú číselnú os (potom rad konverguje vo všetkých bodoch číselnej osi a predpokladá sa, že ). Určenie oblasti konvergencie mocninového radu teda spočíva v určení jeho polomer konvergencie
R a štúdium konvergencie radu na hraniciach intervalu konvergencie (v ). Veta 2. Ak sa všetky koeficienty mocninového radu, počnúc od určitého, líšia od nuly, potom sa jeho polomer konvergencie rovná limitu v pomere absolútnych hodnôt koeficientov spoločných nasledujúcich členov radu. , t.j. Príklad 1. Nájdite oblasť konvergencie mocninného radu Riešenie. Tu Pomocou vzorca (28) nájdeme polomer konvergencie tohto radu: Pozrime sa na konvergenciu radu na koncoch konvergenčného intervalu. Príklad 13 ukazuje, že tento rad konverguje pri X= 1 a líši sa o X= -1. V dôsledku toho je oblasťou konvergencie polovičný interval. Príklad 2. Nájdite oblasť konvergencie mocninného radu Riešenie. Koeficienty radu sú kladné a Nájdite hranicu tohto pomeru, t.j. polomer konvergencie mocninového radu: Pozrime sa na konvergenciu radu na koncoch intervalu. Substitúcia hodnôt X= -1/5 a X= 1/5 v tejto sérii dáva: Prvý z týchto radov konverguje (pozri príklad 5). Ale potom, na základe vety v časti „Absolútna konvergencia“, druhý rad tiež konverguje a oblasťou jeho konvergencie je segment Príklad 3. Nájdite oblasť konvergencie mocninného radu Riešenie. Tu Pomocou vzorca (28) nájdeme polomer konvergencie radu: Poďme študovať konvergenciu radu pre hodnoty . Ich nahradením v tomto rade získame Obidva rady divergujú, pretože nie je splnená nevyhnutná podmienka konvergencie (ich spoločné členy nemajú tendenciu k nule pri ). Na oboch koncoch konvergenčného intervalu teda tento rad diverguje a oblasťou jeho konvergencie je interval. Príklad 5. Nájdite oblasť konvergencie mocninného radu Riešenie. Nájdeme vzťah kde , a Podľa vzorca (28) polomer konvergencie tohto radu to znamená, že rad konverguje len vtedy X= 0 a líši sa pre ostatné hodnoty X. Príklady ukazujú, že na koncoch konvergenčného intervalu sa rad správa inak. V príklade 1 na jednom konci intervalu konvergencie rad konverguje a na druhom diverguje, v príklade 2 konverguje na oboch koncoch a v príklade 3 diverguje na oboch koncoch. Vzorec pre polomer konvergencie mocninového radu sa získa za predpokladu, že všetky koeficienty sériových členov od určitého bodu sa líšia od nuly. Preto je použitie vzorca (28) prípustné len v týchto prípadoch. Ak je táto podmienka porušená, potom by sa mal pomocou polomeru konvergencie mocninového radu hľadať d'Alembertov znak, alebo nahradením premennej transformovaním série na formu, v ktorej je splnená špecifikovaná podmienka. Príklad 6. Nájdite interval konvergencie mocninného radu Riešenie. Táto séria neobsahuje výrazy s nepárnymi stupňami X. Preto transformujeme sériu, nastavenie . Potom dostaneme sériu na nájdenie polomeru konvergencie, ktorého môžeme použiť vzorec (28). Vzhľadom k tomu, , A , Potom polomer konvergencie tohto radu Z rovnosti, ktorú dostaneme , teda tento rad konverguje k intervalu . Nech pre mocenské série polomer konvergencie R> 0, t.j. tento rad konverguje k intervalu . Potom každá hodnota X z konvergenčného intervalu zodpovedá určitému súčtu radu. Preto je súčet mocninových radov funkciou X na konvergenčnom intervale. Označuje to podľa f(X), môžeme napísať rovnosť chápanie v tom zmysle, že súčet série v každom bode X z konvergenčného intervalu sa rovná hodnote funkcie f(X) v tomto bode. V rovnakom zmysle povieme, že mocninný rad (29) konverguje k funkcii f(X) na konvergenčnom intervale. Mimo intervalu konvergencie nemá rovnosť (30) zmysel. Príklad 7. Nájdite súčet mocninových radov Riešenie. Ide o geometrický rad, pre ktorý a= 1, a q= X. Preto je jeho súčet funkciou platí len pre hodnoty, aj keď funkcia Dá sa dokázať, že súčet mocninových radov f(X) je spojitá a diferencovateľná na ľubovoľnom intervale v rámci konvergenčného intervalu, najmä v ktoromkoľvek bode konvergenčného intervalu radu. Uveďme vety o diferenciácii a integrácii mocninných radov po členoch. Veta 1. Mocninný rad (30) v intervale jeho konvergencie môže byť člen po člen neobmedzený počet krát a výsledný mocninný rad má rovnaký polomer konvergencie ako pôvodný rad a ich súčty sú rovné . Veta 2. Výkonový rad (30) je možné integrovať po členoch neobmedzene veľakrát v rozsahu od 0 do X, ak , a výsledný mocninný rad má rovnaký polomer konvergencie ako pôvodný rad a ich súčty sa zodpovedajúco rovnajú Nech je funkcia daná f(X), ktorý je potrebné rozšíriť na mocninový rad, t.j. reprezentovať vo forme (30): Úlohou je určiť koeficienty ……………………………………………….. (31) Za predpokladu rovnosti (30) a (31) X= 0, zistíme Dosadením nájdených výrazov do rovnosti (30) dostaneme Nájdime rozšírenie Maclaurinovho radu niektorých elementárnych funkcií. Príklad 8. Rozšírte funkciu v sérii Maclaurin Riešenie. Derivácie tejto funkcie sa zhodujú so samotnou funkciou: Preto, kedy X= 0 máme Nahradením týchto hodnôt do vzorca (32) získame požadované rozšírenie: Tento rad konverguje na celej číselnej osi (jej polomer konvergencie).
Riešenie. V expanzii (1) nahradíme x -x 2, dostaneme:
, -∞
Riešenie. Máme
Pomocou vzorca (4) môžeme napísať:
nahradením –x namiesto x vo vzorci dostaneme:
Odtiaľto nájdeme: ln(1+x)-ln(1-x) = -
Dostaneme otvorenie zátvoriek, preusporiadanie podmienok série a prinesenie podobných podmienok
. Tento rad konverguje v intervale (-1;1), keďže je získaný z dvoch radov, z ktorých každý konverguje v tomto intervale.
Vzorce (1)-(5) možno použiť aj na rozšírenie zodpovedajúcich funkcií do Taylorovho radu, t.j. pre rozširujúce funkcie v kladných celých číslach ( Ha). Na to je potrebné vykonať také identické transformácie na danej funkcii, aby sme získali jednu z funkcií (1)-(5), v ktorej namiesto X náklady k( Ha) m , kde k je konštantné číslo, m je kladné celé číslo. Často je vhodné vykonať zmenu premennej t=Ha a rozšíriť výslednú funkciu vzhľadom na t v Maclaurinovom rade.
Riešenie. Najprv nájdeme 1-x-6x 2 =(1-3x)(1+2x) , .
na základné:
s konvergenčným regiónom |x|< 1/3.
Riešenie. Tento problém je možné vyriešiť, ako predtým, pomocou definície Taylorovho radu, pre ktorý musíme nájsť deriváty funkcie a ich hodnoty na X=3. Bude však jednoduchšie použiť existujúce rozšírenie (5):
=
Výsledný rad konverguje na alebo –3
Riešenie.
Séria konverguje na , alebo -2< x < 5.
Riešenie. Urobme náhradu t=x-2:
Pomocou rozšírenia (3), v ktorom namiesto x dosadíme π / 4 t, dostaneme:
Výsledný rad konverguje k danej funkcii pri -∞< π / 4 t<+∞, т.е. при (-∞
, (-∞Približné výpočty pomocou mocninových radov
Mocninné rady sú široko používané v približných výpočtoch. S ich pomocou môžete vypočítať hodnoty koreňov, goniometrické funkcie, logaritmy čísel a určité integrály s danou presnosťou. Pri integrácii diferenciálnych rovníc sa používajú aj rady.
Zvážte rozšírenie funkcie v mocninnom rade:
Aby sa vypočítala približná hodnota funkcie v danom bode X, patriace do oblasti konvergencie označeného radu, prvé sú ponechané v jeho expanzii nčlenovia ( n– konečný počet) a zvyšné výrazy sa vyradia:
Pre odhad chyby získanej približnej hodnoty je potrebné odhadnúť vyradený zvyšok rn (x) . Ak to chcete urobiť, použite nasledujúce techniky:
Riešenie. Použime rozšírenie, kde x=1/2 (pozri príklad 5 v predchádzajúcej téme):
Skontrolujeme, či môžeme zvyšok po prvých troch členoch expanzie zahodiť, na to ho vyhodnotíme pomocou súčtu nekonečne klesajúcej geometrickej postupnosti:
Takže môžeme tento zvyšok zahodiť a získať
Riešenie. Použime binomický rad. Keďže 5 3 je kocka celého čísla najbližšie k 130, odporúča sa znázorniť číslo 130 ako 130 = 5 3 +5. 
keďže už štvrtý člen výsledného striedavého radu, ktorý spĺňa Leibnizovo kritérium, je menší ako požadovaná presnosť:
, takže ho a nasledujúce výrazy možno zahodiť.
Mnoho prakticky potrebných určitých alebo nevlastných integrálov nie je možné vypočítať pomocou Newtonovho-Leibnizovho vzorca, pretože jeho aplikácia je spojená s hľadaním primitívnej derivácie, ktorá často nemá vyjadrenie v elementárnych funkciách. Stáva sa aj to, že nájdenie antiderivátu je možné, ale je to zbytočne prácne. Ak je však integrandová funkcia rozšírená do mocninového radu a limity integrácie patria do intervalu konvergencie tohto radu, potom je možný približný výpočet integrálu s vopred stanovenou presnosťou.
Riešenie. Príslušný neurčitý integrál nemožno vyjadriť v elementárnych funkciách, t.j. predstavuje „netrvalý integrál“. Tu nemožno použiť Newtonov-Leibnizov vzorec. Vypočítajme približne integrál.
Rozdelenie pojmov podľa pojmov série pre hriech X na X, dostaneme: 
Integrovaním tohto radu člen po člene (to je možné, pretože limity integrácie patria do intervalu konvergencie tohto radu), dostaneme:
Keďže výsledný rad spĺňa Leibnizove podmienky a na získanie požadovanej hodnoty s danou presnosťou stačí zobrať súčet prvých dvoch členov.
Tak zistíme  .
.
Riešenie.

![]() . Skontrolujeme, či môžeme zahodiť zvyšok po druhom člene výsledného radu.
. Skontrolujeme, či môžeme zahodiť zvyšok po druhom člene výsledného radu.
0,0001<0.001. Следовательно,  .
. ,
tie.
,
tie. =
..
=
..
 má deriváty akéhokoľvek rádu. Je možné ho rozšíriť na mocninový rad? Ak áno, ako tento rad nájdeme? Druhá časť problému je ľahšie vyriešiť, takže začnime s ňou.
má deriváty akéhokoľvek rádu. Je možné ho rozšíriť na mocninový rad? Ak áno, ako tento rad nájdeme? Druhá časť problému je ľahšie vyriešiť, takže začnime s ňou. možno znázorniť ako súčet mocninových radov konvergujúcich v intervale obsahujúcom bod X 0 :
možno znázorniť ako súčet mocninových radov konvergujúcich v intervale obsahujúcom bod X 0 :
 =
..
(*)
=
..
(*) .
. =
..
=
..
 .
. =
..
=
..
 , kde
, kde  .
. , kde
, kde
 ,
,
 ,
,
 ,
…,
,
…,
 ,….,
,…., .
.
3.2. Dostatočné podmienky pre rozložiteľnosť funkcie v Taylorovom rade
 v nejakom okolí bodu x 0 má deriváty až (n+
1) poriadku vrátane, potom v tejto štvrti mámevzorec
Taylor
v nejakom okolí bodu x 0 má deriváty až (n+
1) poriadku vrátane, potom v tejto štvrti mámevzorec
Taylor

 .
.
 definuje chybu, ktorú dostaneme, nahraďte funkciu f(X)
polynóm S n (X).
definuje chybu, ktorú dostaneme, nahraďte funkciu f(X)
polynóm S n (X).
 , To
, To  ,tie. funkcia je rozšírená do Taylorovho radu. Naopak, ak
,tie. funkcia je rozšírená do Taylorovho radu. Naopak, ak  , To
, To  .
. , KdeR n (X) je zvyšok Taylorovho radu.
, KdeR n (X) je zvyšok Taylorovho radu. , To v tomto okolí funkcia expanduje do Taylorovho radu.
, To v tomto okolí funkcia expanduje do Taylorovho radu. alebo
alebo
 .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]() :
:![]()
![]() ,
,![]()
![]()
![]()
Súčet mocninových radov. Diferenciácia a integrácia mocninových radov
![]()
![]() . Rad konverguje, ak , a je jeho intervalom konvergencie. Preto rovnosť
. Rad konverguje, ak , a je jeho intervalom konvergencie. Preto rovnosť![]()
![]() definované pre všetky hodnoty X, okrem X= 1.
definované pre všetky hodnoty X, okrem X= 1.
Rozšírenie funkcií do mocninových radov
![]() riadok (30). Aby sme to dosiahli, rozlišovaním rovnosti (30) medzi členmi dôsledne nachádzame:
riadok (30). Aby sme to dosiahli, rozlišovaním rovnosti (30) medzi členmi dôsledne nachádzame:![]()
![]()
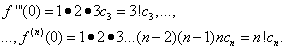
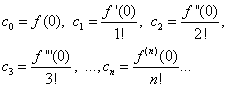
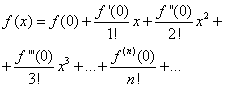 (32)
(32)
![]() (33)
(33)

