Príklady určitého integrálu po častiach. Riešenie integrálov online
Predtým sme pre danú funkciu, riadenú rôznymi vzorcami a pravidlami, našli jej deriváciu. Derivát má množstvo aplikácií: je to rýchlosť pohybu (alebo všeobecnejšie rýchlosť akéhokoľvek procesu); sklon dotyčnice ku grafu funkcie; pomocou derivácie môžete skúmať funkciu pre monotónnosť a extrémy; Pomáha riešiť problémy s optimalizáciou.
Ale spolu s problémom nájdenia rýchlosti zo známeho zákona o pohybe existuje aj inverzný problém - problém obnovenia zákona o pohybe zo známej rýchlosti. Pozrime sa na jeden z týchto problémov.
Príklad 1 Hmotný bod sa pohybuje po priamke, rýchlosť jeho pohybu v čase t je daná vzorcom v=gt. Nájdite zákon pohybu.
Riešenie. Nech s = s(t) je požadovaný pohybový zákon. Je známe, že s"(t) = v(t). Na vyriešenie problému si teda musíte vybrať funkciu s = s(t), ktorej derivácia sa rovná gt. Je ľahké uhádnuť, že \( s(t) = \frac(gt^ 2)(2) \) Naozaj
\(s"(t) = \left(\frac(gt^2)(2) \right)" = \frac(g)(2)(t^2)" = \frac(g)(2) \ cdot 2t=gt\)
Odpoveď: \(s(t) = \frac(gt^2)(2) \)
Hneď si všimneme, že príklad je vyriešený správne, ale neúplne. Dostali sme \(s(t) = \frac(gt^2)(2) \). V skutočnosti má problém nekonečne veľa riešení: akákoľvek funkcia tvaru \(s(t) = \frac(gt^2)(2) + C \), kde C je ľubovoľná konštanta, môže slúžiť ako zákon pohyb, pretože \(\left (\frac(gt^2)(2) +C \right)" = gt \)
Aby sme problém upresnili, museli sme opraviť počiatočnú situáciu: uviesť súradnicu pohybujúceho sa bodu v určitom časovom bode, napríklad v t = 0. Ak povedzme s(0) = s 0 , potom od rovnosť s(t) = (gt 2)/2 + C dostaneme: s(0) = 0 + C, teda C = s 0 . Teraz je pohybový zákon jednoznačne definovaný: s(t) = (gt 2)/2 + s 0 .
V matematike sa vzájomne inverzným operáciám priraďujú rôzne názvy, prichádzajú so špeciálnymi zápismi, napríklad: kvadratúra (x 2) a extrakcia druhej odmocniny (\(\sqrt(x) \)), sínus (sin x) a arcsínus ( arcsin x) atď. Proces hľadania derivácie vzhľadom na danú funkciu sa nazýva diferenciácie a inverzná operácia, t.j. proces hľadania funkcie danou deriváciou, - integrácia.
Samotný výraz „derivát“ možno odôvodniť „svetským spôsobom“: funkcia y \u003d f (x) „vyprodukuje do sveta“ novú funkciu y“ \u003d f „(x). Funkcia y \u003d f (x) pôsobí ako „rodič“, ale matematici ju, samozrejme, nenazývajú „rodič“ alebo „producent“, hovoria, že je to vo vzťahu k funkcii y “ = f" (x), primárny obrázok alebo priradený prvok.
Definícia. Funkcia y = F(x) sa nazýva primitívna funkcia pre funkciu y = f(x) na intervale X, ak \(x \in X \) spĺňa rovnosť F"(x) = f(x)
V praxi interval X zvyčajne nie je špecifikovaný, ale implikovaný (ako prirodzená doména funkcie).
Uveďme si príklady.
1) Funkcia y \u003d x 2 je priradením funkcie y \u003d 2x, pretože pre ľubovoľné x platí rovnosť (x 2)" \u003d 2x
2) Funkcia y \u003d x 3 je priradením funkcie y \u003d 3x 2, pretože pre ľubovoľné x platí rovnosť (x 3)" \u003d 3x 2
3) Funkcia y \u003d sin (x) je priradením funkcie y \u003d cos (x), pretože pre ľubovoľné x platí rovnosť (sin (x)) "= cos (x)
Pri hľadaní primitívnych, ale aj derivátov sa nepoužívajú len vzorce, ale aj niektoré pravidlá. Sú priamo spojené s príslušnými pravidlami pre výpočet derivátov.
Vieme, že derivácia súčtu sa rovná súčtu derivácií. Toto pravidlo generuje zodpovedajúce pravidlo na hľadanie primitívnych prvkov.
Pravidlo 1 Prvok súčtu sa rovná súčtu primitív.
Vieme, že konštantný faktor možno vyňať zo znamienka derivácie. Toto pravidlo generuje zodpovedajúce pravidlo na hľadanie primitívnych prvkov.
Pravidlo 2 Ak je F(x) primitívom pre f(x), potom kF(x) je primitívom pre kf(x).
Veta 1. Ak y = F(x) je primitívna funkcia pre funkciu y = f(x), potom primitívna funkcia pre funkciu y = f(kx + m) je funkcia \(y=\frac(1)(k)F (kx+m) \)
Veta 2. Ak y = F(x) je primitívna funkcia pre funkciu y = f(x) na intervale X, potom funkcia y = f(x) má nekonečne veľa primitív a všetky majú tvar y = F(x) + C.
Integračné metódy
Variabilná náhradná metóda (substitučná metóda)
Metóda substitučnej integrácie spočíva v zavedení novej integračnej premennej (t. j. substitúcie). V tomto prípade sa daný integrál redukuje na nový integrál, ktorý je tabuľkový alebo naň redukovateľný. Neexistujú žiadne všeobecné metódy na výber substitúcií. Schopnosť správne určiť substitúciu sa získava praxou.
Nech je potrebné vypočítať integrál \(\textstyle \int F(x)dx \). Urobme substitúciu \(x= \varphi(t) \), kde \(\varphi(t) \) je funkcia, ktorá má spojitú deriváciu.
Potom \(dx = \varphi " (t) \cdot dt \) a na základe vlastnosti invariantnosti neurčitého integrálneho integračného vzorca získame substitučný integračný vzorec:
\(\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt \)
Integrácia výrazov ako \(\textstyle \int \sin^n x \cos^m x dx \)
Ak je m nepárne, m > 0, potom je vhodnejšie urobiť substitúciu sin x = t.
Ak je n nepárne, n > 0, potom je vhodnejšie urobiť substitúciu cos x = t.
Ak sú n a m párne, potom je vhodnejšie vykonať substitúciu tg x = t.
Integrácia po častiach
Integrácia podľa častí - použitie nasledujúceho vzorca pre integráciu:
\(\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du \)
alebo:
\(\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx \)
Tabuľka neurčitých integrálov (antiderivátov) niektorých funkcií
$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) +C \;\; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(arcsin) x +C $$ $$ \int \frac(dx)(1+x^2 ) = \text(arctg) x +C $$ $$ \int \text(ch) x dx = \text(sh) x +C $$ $$ \int \text(sh) x dx = \text(ch )x+C $$Integrácia po častiach. Príklady riešení
Ahoj zas. Dnes sa v lekcii naučíme, ako integrovať po častiach. Metóda integrácie po častiach je jedným zo základných kameňov integrálneho počtu. Na teste, skúške je študentovi takmer vždy ponúknuté riešenie integrálov typu: najjednoduchší integrál (pozri článok) alebo integrál na zmenu premennej (pozri článok) alebo integrál len na spôsob integrácie po častiach.
Ako vždy, po ruke by malo byť: Tabuľka integrálov A Tabuľka derivátov. Ak ich ešte nemáte, navštívte prosím sklad mojej stránky: Matematické vzorce a tabuľky. Nebudem sa unavovať opakovaním - je lepšie vytlačiť všetko. Pokúsim sa prezentovať všetok materiál konzistentným, jednoduchým a prístupným spôsobom, pri integrácii po častiach nie sú žiadne zvláštne ťažkosti.
Aký problém rieši integrácia po častiach? Metóda integrácie po častiach rieši veľmi dôležitý problém, umožňuje integrovať niektoré funkcie, ktoré nie sú v tabuľke, práca funkcie av niektorých prípadoch aj súkromné. Ako si pamätáme, neexistuje žiadny vhodný vzorec: ![]() . Ale je tu tento:
. Ale je tu tento: ![]() je vzorec pre integráciu po častiach osobne. Viem, viem, ste jediný - s ňou budeme pracovať celú lekciu (už je to jednoduchšie).
je vzorec pre integráciu po častiach osobne. Viem, viem, ste jediný - s ňou budeme pracovať celú lekciu (už je to jednoduchšie).
A hneď zoznam v štúdiu. Integrály nasledujúcich typov sú prevzaté časťami:
1) , ![]() , - logaritmus, logaritmus vynásobený nejakým polynómom.
, - logaritmus, logaritmus vynásobený nejakým polynómom.
2) ,![]() je exponenciálna funkcia vynásobená nejakým polynómom. Patria sem aj integrály ako - exponenciálna funkcia vynásobená polynómom, ale v praxi je to 97 percent, pod integrálom sa vychvaľuje pekné písmeno „e“. ... článok sa ukáže ako niečo lyrické, ach áno ... prišla jar.
je exponenciálna funkcia vynásobená nejakým polynómom. Patria sem aj integrály ako - exponenciálna funkcia vynásobená polynómom, ale v praxi je to 97 percent, pod integrálom sa vychvaľuje pekné písmeno „e“. ... článok sa ukáže ako niečo lyrické, ach áno ... prišla jar.
3) , ![]() , sú goniometrické funkcie vynásobené nejakým polynómom.
, sú goniometrické funkcie vynásobené nejakým polynómom.
4) , - inverzné goniometrické funkcie („oblúky“), „oblúky“, vynásobené nejakým polynómom.
Niektoré zlomky sa tiež berú po častiach, podrobne zvážime aj zodpovedajúce príklady.
Integrály logaritmov
Príklad 1
klasické. Z času na čas sa tento integrál nájde v tabuľkách, ale je nežiaduce použiť hotovú odpoveď, keďže učiteľ má na jar beri-beri a bude veľa nadávať. Pretože uvažovaný integrál nie je v žiadnom prípade tabuľkový - berie sa po častiach. Rozhodujeme sa:
Pre medziľahlé vysvetlenia prerušujeme riešenie.
Na integráciu po častiach používame vzorec: ![]()
Vzorec sa aplikuje zľava doprava
Pozeráme sa na ľavú stranu:. Je zrejmé, že v našom príklade (a vo všetkých ostatných, ktoré budeme zvažovať), je potrebné niečo označiť a niečo pomocou .
V integráloch uvažovaného typu vždy označujeme logaritmus.
Technicky je návrh riešenia realizovaný nasledovne, do stĺpca píšeme:
To znamená, že sme označili logaritmus a pre - zvyšná časť integrand.
Ďalší krok: nájdite rozdiel:

Diferenciál je takmer rovnaký ako derivácia, ako ho nájsť sme už rozoberali v predchádzajúcich lekciách.
Teraz nájdeme funkciu. Na nájdenie funkcie je potrebné integrovať pravá strana nižšia rovnosť:

Teraz otvoríme naše riešenie a zostrojíme pravú stranu vzorca: .
Mimochodom, tu je príklad konečného riešenia s niekoľkými poznámkami:

Jediný moment v produkte som okamžite preusporiadal a keďže je zvykom písať multiplikátor pred logaritmus.
Ako vidíte, použitie vzorca integrácie podľa častí v podstate zredukovalo naše riešenie na dva jednoduché integrály.
Upozorňujeme, že v niektorých prípadoch hneď po pri použití vzorca sa nevyhnutne uskutoční zjednodušenie pod zvyšným integrálom - v uvažovanom príklade sme integrand znížili o "x".
Urobme kontrolu. Aby ste to dosiahli, musíte použiť derivát odpovede:
Bol získaný pôvodný integrand, čo znamená, že integrál bol vyriešený správne.
Pri overovaní sme použili pravidlo diferenciácie produktov: ![]() . A to nie je náhoda.
. A to nie je náhoda.
Vzorec integrácie podľa častí ![]() a vzorec
a vzorec ![]() Ide o dve vzájomne inverzné pravidlá.
Ide o dve vzájomne inverzné pravidlá.
Príklad 2
Nájdite neurčitý integrál.
Integrand je súčinom logaritmu a polynómu.
My rozhodujeme.
![]()
Ešte raz podrobne opíšem postup uplatňovania pravidla, v budúcnosti budú príklady vyhotovené stručnejšie a ak máte problémy s riešením sami, musíte sa vrátiť k prvým dvom príkladom lekcie .
Ako už bolo spomenuté, je potrebné určiť logaritmus (na tom, že je v určitej miere, nezáleží). Označujeme zvyšná časť integrand.
Do stĺpca píšeme:
Najprv nájdeme diferenciál:

Tu používame pravidlo diferenciácie komplexnej funkcie ![]() . Nie je náhoda, že hneď na prvej lekcii témy Neurčitý integrál. Príklady riešení Zameral som sa na to, že na zvládnutie integrálov treba „dostať do ruky“ derivácie. Deriváty budú musieť čeliť viac ako raz.
. Nie je náhoda, že hneď na prvej lekcii témy Neurčitý integrál. Príklady riešení Zameral som sa na to, že na zvládnutie integrálov treba „dostať do ruky“ derivácie. Deriváty budú musieť čeliť viac ako raz.
Teraz nájdeme funkciu , na to integrujeme pravá strana nižšia rovnosť:

Na integráciu sme použili najjednoduchší tabuľkový vzorec ![]()
Teraz ste pripravení použiť vzorec ![]() . Otvoríme ho „hviezdičkou“ a „navrhneme“ riešenie v súlade s pravou stranou:
. Otvoríme ho „hviezdičkou“ a „navrhneme“ riešenie v súlade s pravou stranou:
Pod integrálom máme opäť polynóm na logaritme! Preto sa riešenie opäť preruší a druhýkrát sa použije pravidlo integrácie po častiach. Nezabudnite, že v podobných situáciách sa logaritmus vždy označuje.

Bolo by pekné, keby ste v tomto bode boli schopní nájsť najjednoduchšie integrály a derivácie ústne.

(1) Nenechajte sa zmiasť v znameniach! Veľmi často sa tu stráca mínus, všimnite si tiež, že platí mínus všetkým držiak  a tieto zátvorky je potrebné správne otvoriť.
a tieto zátvorky je potrebné správne otvoriť.
(2) Rozbaľte zátvorky. Posledný integrál zjednodušíme.
(3) Vezmeme posledný integrál.
(4) „Prečesanie“ odpovede.
Potreba aplikovať pravidlo integrácie po častiach dvakrát (alebo dokonca trikrát) nie je nezvyčajná.
A teraz pár príkladov pre nezávislé riešenie:
Príklad 3
Nájdite neurčitý integrál.
Tento príklad je riešený zmenou premennej metódy (alebo pripočítaním pod diferenciálne znamienko)! A prečo nie - môžete to skúsiť po častiach, dostanete vtipnú vec.
Príklad 4
Nájdite neurčitý integrál.
Ale tento integrál je integrovaný po častiach (sľúbený zlomok).
Toto sú príklady na samoriešenie, riešenia a odpovede na konci hodiny.
Zdá sa, že v príkladoch 3,4 sú integrandy podobné, ale metódy riešenia sú odlišné! To je práve hlavná náročnosť zvládnutia integrálov – ak si zvolíte nesprávnu metódu riešenia integrálu, môžete sa s tým popasovať celé hodiny, ako so skutočným hlavolamom. Preto čím viac budete riešiť rôzne integrály, tým lepšie, tým ľahšie bude test a skúška. Navyše v druhom ročníku budú diferenciálne rovnice a bez skúseností s riešením integrálov a derivácií tam nie je čo robiť.
Logaritmicky možno viac než dosť. Na občerstvenie si tiež pamätám, že študenti techniky nazývajú ženské prsia logaritmy =). Mimochodom, je užitočné poznať naspamäť grafy hlavných elementárnych funkcií: sínus, kosínus, arkustangens, exponent, polynómy tretieho, štvrtého stupňa atď. Nie, samozrejme, kondóm na zemeguli
Nebudem ťahať, ale teraz si z rubriky budete veľa pamätať Grafy a funkcie =).
Integrály exponentu násobené polynómom
Všeobecné pravidlo:
Príklad 5
Nájdite neurčitý integrál.
![]()
Pomocou známeho algoritmu integrujeme po častiach:


Ak máte nejaké problémy s integrálom, mali by ste sa vrátiť k článku Metóda zmeny premennej v neurčitom integráli.
Jediná ďalšia vec, ktorú musíte urobiť, je „učesať“ odpoveď:

Ak však vaša technika výpočtu nie je príliš dobrá, ponechajte ako odpoveď najziskovejšiu možnosť. ![]() alebo dokonca
alebo dokonca ![]()
To znamená, že príklad sa považuje za vyriešený, keď sa vezme posledný integrál. Nebude to chyba, je to ďalšia vec, ktorú môže učiteľ požiadať, aby zjednodušil odpoveď.
Príklad 6
Nájdite neurčitý integrál.
Toto je príklad „urob si sám“. Tento integrál je integrovaný dvakrát po častiach. Osobitná pozornosť by sa mala venovať znakom - je ľahké sa v nich zmiasť, pamätáme si to aj na zložitú funkciu.
Viac o vystavovateľovi nie je čo povedať. Len dodám, že exponenciála a prirodzený logaritmus sú vzájomne inverzné funkcie, toto som ja k téme zábavných grafov vyššej matematiky =) Stop-stop, nebojte sa, prednášajúci je triezvy.
Integrály goniometrických funkcií násobené polynómom
Všeobecné pravidlo: vždy znamená polynóm
Príklad 7
Nájdite neurčitý integrál.
![]()
Integrácia podľa častí:


Hmmm...a niet čo komentovať.
Príklad 8
Nájdite neurčitý integrál ![]()
Toto je príklad riešenia „urob si sám“.
Príklad 9
Nájdite neurčitý integrál
Ďalší príklad so zlomkom. Rovnako ako v predchádzajúcich dvoch príkladoch je polynóm označený ako.
Integrácia podľa častí: 

Ak máte nejaké ťažkosti alebo nedorozumenia s hľadaním integrálu, potom odporúčam lekciu navštíviť Integrály goniometrických funkcií.
Príklad 10
Nájdite neurčitý integrál ![]()
Toto je príklad „urob si sám“.
Tip: pred použitím metódy integrácie podľa častí by ste mali použiť nejaký trigonometrický vzorec, ktorý zmení súčin dvoch goniometrických funkcií na jednu funkciu. Vzorec je možné použiť aj pri aplikácii metódy integrácie po častiach, pre koho je to výhodnejšie.
To je snáď všetko v tomto odseku. Z nejakého dôvodu som si spomenul na vetu z hymny katedry fyziky a matematiky „A sínusový graf vlna za vlnou prebieha pozdĺž osi x“.
Integrály inverzných goniometrických funkcií.
Integrály inverzných goniometrických funkcií násobené polynómom
Všeobecné pravidlo: vždy znamená inverznú goniometrickú funkciu.
Pripomínam, že inverzné goniometrické funkcie zahŕňajú arksínus, arkkozín, arkustangens a arkkotangens. Pre stručnosť ich budem označovať ako „oblúky“

 na výpočet integrálu
na výpočet integrálu  , ktorý sa ukazuje ako jednoduchší ako daný.
, ktorý sa ukazuje ako jednoduchší ako daný. ,
, ,
, , Kde
, Kde  - polynóm,
- polynóm,  - číslo sa nerovná nule
- číslo sa nerovná nule označujú polynóm
označujú polynóm 
 .
. ,
, ,
, ,
, ,
, , Kde
, Kde  je polynóm.
je polynóm. určiť
určiť  , a zvyšok integrandu cez
, a zvyšok integrandu cez  :
: ,
, , Kde
, Kde  - čísla.
- čísla. určiť
určiť  a použiť vzorec integrácie po častiach dvakrát, čím sa vrátime k pôvodnému integrálu, po ktorom sa pôvodný integrál vyjadrí z rovnosti.
a použiť vzorec integrácie po častiach dvakrát, čím sa vrátime k pôvodnému integrálu, po ktorom sa pôvodný integrál vyjadrí z rovnosti. ; b)
; b)  .
.
 , Kde
, Kde  je polynóm stupňa
je polynóm stupňa  ,
, je polynóm stupňa
je polynóm stupňa
 .
. inak (ak
inak (ak  ) racionálny zlomok sa nazýva nesprávne.
) racionálny zlomok sa nazýva nesprávne. a vlastný racionálny zlomok delením čitateľa menovateľom podľa pravidla delenia polynómov:
a vlastný racionálny zlomok delením čitateľa menovateľom podľa pravidla delenia polynómov: ,
, je celá časť delenia,
je celá časť delenia,  je správny racionálny zlomok,
je správny racionálny zlomok,  - zvyšok divízie.
- zvyšok divízie. ;
; ;
; ;
; ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 sú reálne čísla a
sú reálne čísla a  (t. j. štvorcová trojčlenka v menovateli III a IV zlomkov nemá korene – diskriminant je záporný) sú tzv. najjednoduchšie racionálne zlomky I, II, III a IV typy.
(t. j. štvorcová trojčlenka v menovateli III a IV zlomkov nemá korene – diskriminant je záporný) sú tzv. najjednoduchšie racionálne zlomky I, II, III a IV typy. .
. .
. . Integrál po substitúcii je rozdelený na dva integrály. Prvý integrál sa vypočíta extrahovaním derivácie menovateľa v čitateli, čím sa získa tabuľkový integrál, a druhý integrál sa prevedie do tvaru
. Integrál po substitúcii je rozdelený na dva integrály. Prvý integrál sa vypočíta extrahovaním derivácie menovateľa v čitateli, čím sa získa tabuľkový integrál, a druhý integrál sa prevedie do tvaru  , pretože
, pretože  , ktorý dáva aj tabuľkový integrál.
, ktorý dáva aj tabuľkový integrál.

 ;
; . Integrál po substitúcii je rozdelený na dva integrály. Prvý integrál sa vypočíta dosadením
. Integrál po substitúcii je rozdelený na dva integrály. Prvý integrál sa vypočíta dosadením  , a druhý pomocou rekurentných vzťahov.
, a druhý pomocou rekurentných vzťahov. ; b)
; b)  ; V)
; V)  .
. .
. zodpovedá jednému zlomku formulára
zodpovedá jednému zlomku formulára  ;
; zodpovedajúca suma
zodpovedajúca suma  zlomky formulára
zlomky formulára zodpovedá zlomku formy
zodpovedá zlomku formy  ;
; zodpovedajúca suma
zodpovedajúca suma  zlomky formulára
zlomky formulára . Vyrovnanie koeficientov pri rovnakých mocninách
. Vyrovnanie koeficientov pri rovnakých mocninách  v polynómoch ľavej a pravej časti získame sústavu lineárnych rovníc. Pri riešení systému určíme neisté koeficienty.
v polynómoch ľavej a pravej časti získame sústavu lineárnych rovníc. Pri riešení systému určíme neisté koeficienty. na ľavú a pravú stranu ľubovoľného čísla dostaneme správnu rovnosť, ktorá je lineárna vzhľadom na neznáme koeficienty. Nahradením toľkých hodnôt
na ľavú a pravú stranu ľubovoľného čísla dostaneme správnu rovnosť, ktorá je lineárna vzhľadom na neznáme koeficienty. Nahradením toľkých hodnôt  , koľko neznámych koeficientov, dostaneme sústavu lineárnych rovníc. Namiesto
, koľko neznámych koeficientov, dostaneme sústavu lineárnych rovníc. Namiesto  v ľavej a pravej časti možno dosadiť ľubovoľné čísla, vhodnejšie je však dosadiť odmocniny menovateľov zlomkov.
v ľavej a pravej časti možno dosadiť ľubovoľné čísla, vhodnejšie je však dosadiť odmocniny menovateľov zlomkov. ; b)
; b)  ; V)
; V)  .
. .
.
 .
. , dostaneme:
, dostaneme:



 .
. .
. .
. .
. , dostaneme systém:
, dostaneme systém:








 .
.
 .
. .
. .
. čiastkové hodnoty, pri ktorých faktory miznú, t.j. tieto hodnoty dosadíme do posledného výrazu a dostaneme tri rovnice:
čiastkové hodnoty, pri ktorých faktory miznú, t.j. tieto hodnoty dosadíme do posledného výrazu a dostaneme tri rovnice:
 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.


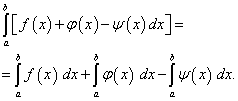 (42)
(42)




