Rozszerzenie cos w szeregu Taylora. Rozszerzenie funkcji w szeregi potęgowe
16.1. Rozwinięcie funkcji elementarnych w szereg Taylora i
Maclauri
Pokażmy, że jeśli na zbiorze zdefiniowana jest dowolna funkcja  , w pobliżu punktu
, w pobliżu punktu  ma wiele pochodnych i jest sumą szeregu potęgowego:
ma wiele pochodnych i jest sumą szeregu potęgowego:
wtedy możesz znaleźć współczynniki tej serii.
Podstaw w szeregu potęgowym  . Następnie
. Następnie  .
.
Znajdź pierwszą pochodną funkcji  :
:
Na  :
: .
.
Dla drugiej pochodnej otrzymujemy:
Na  :
: .
.
Kontynuacja tej procedury n gdy otrzymamy:  .
.
W ten sposób otrzymaliśmy szereg potęgowy postaci:


 ,
,
który jest nazywany blisko Taylor dla funkcji  wokół punktu
wokół punktu  .
.
Szczególnym przypadkiem serii Taylora jest Seria Maclaurina w  :
:



Pozostałą część szeregu Taylora (Maclaurina) otrzymuje się przez odrzucenie szeregu głównego n pierwsze warunki i jest oznaczone jako  . Następnie funkcja
. Następnie funkcja  można zapisać jako sumę n pierwsi członkowie serii
można zapisać jako sumę n pierwsi członkowie serii  a reszta
a reszta  :,
:,
 .
.
Reszta to zwykle  wyrażone w różnych formułach.
wyrażone w różnych formułach.
Jeden z nich jest w formie Lagrange'a:
 , gdzie
, gdzie  .
. .
.
Zauważ, że w praktyce seria Maclaurin jest używana częściej. Tak więc, aby napisać funkcję  w postaci sumy szeregu potęgowego konieczne jest:
w postaci sumy szeregu potęgowego konieczne jest:
1) znaleźć współczynniki szeregu Maclaurina (Taylora);
2) znaleźć obszar zbieżności wynikowych szeregów potęgowych;
3) udowodnić, że dany szereg jest zbieżny do funkcji  .
.
Twierdzenie1
(konieczny i wystarczający warunek konwergencji szeregu Maclaurina). Niech promień zbieżności szeregu  . Aby ta seria była zbieżna w przedziale
. Aby ta seria była zbieżna w przedziale  funkcjonować
funkcjonować  , konieczne i wystarczające jest spełnienie następującego warunku:
, konieczne i wystarczające jest spełnienie następującego warunku:  w określonym przedziale.
w określonym przedziale.
Twierdzenie 2. Jeżeli pochodne dowolnego rzędu funkcji  w pewnym przedziale
w pewnym przedziale  ograniczone w wartości bezwzględnej do tej samej liczby M, to znaczy
ograniczone w wartości bezwzględnej do tej samej liczby M, to znaczy  , to w tym przedziale funkcja
, to w tym przedziale funkcja  można rozszerzyć w serii Maclaurin.
można rozszerzyć w serii Maclaurin.
Przykład1
.
Rozwiń w serii Taylora wokół punktu  funkcjonować.
funkcjonować.
Rozwiązanie.
 .
.
 ,;
,;
 ,
, ;
;
 ,
, ;
;
 ,
,
.......................................................................................................................................
 ,
, ;
;
Obszar konwergencji  .
.
Przykład2
.
Rozwiń funkcję  w serii Taylora wokół punktu
w serii Taylora wokół punktu  .
.
Rozwiązanie:
Znajdujemy wartość funkcji i jej pochodnych w  .
.
 ,
, ;
;
 ,
, ;
;
...........……………………………
 ,
, .
.
Zastąp te wartości z rzędu. Otrzymujemy:
lub  .
.
Znajdźmy obszar zbieżności tej serii. Zgodnie z testem d'Alemberta szereg jest zbieżny, jeśli
 .
.
Dlatego dla każdego  granica ta jest mniejsza niż 1, a zatem obszar zbieżności szeregu będzie wynosił:
granica ta jest mniejsza niż 1, a zatem obszar zbieżności szeregu będzie wynosił:  .
.
Rozważmy kilka przykładów rozszerzenia w szereg Maclaurina podstawowych funkcji elementarnych. Przypomnijmy, że seria Maclaurin:


 .
.
zbiega się w przedziale  funkcjonować
funkcjonować  .
.
Zwróć uwagę, że aby rozszerzyć funkcję na serię, konieczne jest:
a) znaleźć współczynniki szeregu Maclaurina dla danej funkcji;
b) obliczyć promień zbieżności dla otrzymanego szeregu;
c) udowodnić, że wynikowy szereg jest zbieżny do funkcji  .
.
Przykład 3 Rozważ funkcję  .
.
Rozwiązanie.
Obliczmy wartość funkcji i jej pochodnych dla  .
.
Wówczas współczynniki liczbowe szeregu mają postać:
dla kazdego n. Podstawiamy znalezione współczynniki w szereg Maclaurina i otrzymujemy: 
Znajdź promień zbieżności powstałego szeregu, a mianowicie:
 .
.
Dlatego szereg zbiega się na przedziale  .
.
Ta seria zbiega się z funkcją  dla dowolnych wartości
dla dowolnych wartości  , bo na dowolnym interwale
, bo na dowolnym interwale  funkcjonować
funkcjonować  a jego pochodne wartości bezwzględnej są ograniczone liczbą
a jego pochodne wartości bezwzględnej są ograniczone liczbą  .
.
Przykład4
.
Rozważ funkcję  .
.
Rozwiązanie.
 :
:

Łatwo zauważyć, że pochodne parzystego rzędu  i pochodne nieparzystego rzędu. Podstawiamy znalezione współczynniki w szereg Maclaurina i otrzymujemy rozszerzenie:
i pochodne nieparzystego rzędu. Podstawiamy znalezione współczynniki w szereg Maclaurina i otrzymujemy rozszerzenie:
Znajdźmy przedział zbieżności tego szeregu. Według d'Alemberta:
dla kazdego  . Dlatego szereg zbiega się na przedziale
. Dlatego szereg zbiega się na przedziale  .
.
Ta seria zbiega się z funkcją  , ponieważ wszystkie jego pochodne są ograniczone do jednego.
, ponieważ wszystkie jego pochodne są ograniczone do jednego.
Przykład5
.
 .
.
Rozwiązanie.
Znajdźmy wartość funkcji i jej pochodnych w  :
:

Zatem współczynniki tej serii:  oraz
oraz  , W konsekwencji:
, W konsekwencji:
Podobnie z poprzednią serią, obszar konwergencji  . Szereg zbiega się z funkcją
. Szereg zbiega się z funkcją  , ponieważ wszystkie jego pochodne są ograniczone do jednego.
, ponieważ wszystkie jego pochodne są ograniczone do jednego.
Zauważ, że funkcja  nieparzyste i szeregowe rozwinięcie w nieparzystych potęgach, funkcja
nieparzyste i szeregowe rozwinięcie w nieparzystych potęgach, funkcja  – parzystość i ekspansja w serii w równych potęgach.
– parzystość i ekspansja w serii w równych potęgach.
Przykład6
.
Szeregi dwumianowe:  .
.
Rozwiązanie.
Znajdźmy wartość funkcji i jej pochodnych w  :
:

To pokazuje że:

Podstawiamy te wartości współczynników w szereg Maclaurina i otrzymujemy rozwinięcie tej funkcji w szereg potęgowy:
Znajdźmy promień zbieżności tego szeregu:

Dlatego szereg zbiega się na przedziale  . W punktach granicznych w
. W punktach granicznych w  oraz
oraz  szeregi mogą lub nie mogą być zbieżne w zależności od wykładnika
szeregi mogą lub nie mogą być zbieżne w zależności od wykładnika  .
.
Badany szereg jest zbieżny na przedziale  funkcjonować
funkcjonować  czyli suma szeregu
czyli suma szeregu  w
w  .
.
Przykład7
.
Rozwińmy funkcję w szeregu Maclaurina  .
.
Rozwiązanie.
Aby rozszerzyć tę funkcję na szereg, używamy szeregu dwumianowego dla  . Otrzymujemy:
. Otrzymujemy: 
Na podstawie własności szeregu potęgowego (szereg potęgowy może być całkowany w obszarze jego zbieżności) znajdujemy całkę lewej i prawej części tego szeregu:
Znajdź obszar zbieżności tej serii:  ,
,
czyli obszar zbieżności tego szeregu jest przedziałem  . Wyznaczmy zbieżność szeregu na końcach przedziału. Na
. Wyznaczmy zbieżność szeregu na końcach przedziału. Na 
 . Ten szereg jest szeregiem harmonicznym, to znaczy rozbieżnym. Na
. Ten szereg jest szeregiem harmonicznym, to znaczy rozbieżnym. Na  otrzymujemy szereg liczb ze wspólnym terminem
otrzymujemy szereg liczb ze wspólnym terminem  .
.
Seria Leibniza zbiega się. Zatem obszarem zbieżności tego szeregu jest przedział  .
.
16.2. Zastosowanie szeregów potęgowych w obliczeniach przybliżonych
Szeregi potęgowe odgrywają niezwykle ważną rolę w obliczeniach przybliżonych. Za ich pomocą opracowano tabele funkcji trygonometrycznych, tabele logarytmów, tabele wartości innych funkcji, które są wykorzystywane w różnych dziedzinach wiedzy, na przykład w teorii prawdopodobieństwa i statystyce matematycznej. Ponadto rozwinięcie funkcji w szereg potęgowy jest przydatne do ich teoretycznego badania. Głównym problemem przy stosowaniu szeregów potęgowych w obliczeniach przybliżonych jest kwestia oszacowania błędu przy zastępowaniu sumy szeregu przez sumę jego pierwszego n członków.
Rozważ dwa przypadki:
funkcja jest rozszerzona na szereg naprzemienny;
funkcja jest rozszerzona do serii znaków stałych.
Obliczanie za pomocą szeregów przemiennych
Niech funkcja  rozszerzona na serię o zmiennej mocy. Następnie przy obliczaniu tej funkcji dla określonej wartości
rozszerzona na serię o zmiennej mocy. Następnie przy obliczaniu tej funkcji dla określonej wartości  otrzymujemy szereg liczb, do którego możemy zastosować test Leibniza. Zgodnie z tym kryterium, jeżeli sumę szeregu zastępuje się sumą jego pierwszego n członków, to błąd bezwzględny nie przekracza pierwszego członu pozostałej części tego szeregu, czyli:
otrzymujemy szereg liczb, do którego możemy zastosować test Leibniza. Zgodnie z tym kryterium, jeżeli sumę szeregu zastępuje się sumą jego pierwszego n członków, to błąd bezwzględny nie przekracza pierwszego członu pozostałej części tego szeregu, czyli:  .
.
Przykład8
.
Oblicz  z dokładnością 0,0001.
z dokładnością 0,0001.
Rozwiązanie.
Serii Maclaurin będziemy używać do  , zastępując wartość kąta w radianach:
, zastępując wartość kąta w radianach:

Jeśli porównamy pierwszy i drugi człon szeregu z zadaną dokładnością, to: .
Trzeci termin ekspansji:
mniejsza niż określona dokładność obliczeń. Dlatego, aby obliczyć  wystarczy pozostawić dwa terminy serii, tj.
wystarczy pozostawić dwa terminy serii, tj.
 .
.
W ten sposób  .
.
Przykład9
.
Oblicz  z dokładnością 0,001.
z dokładnością 0,001.
Rozwiązanie.
Użyjemy wzoru na szereg dwumianowy. Do tego piszemy  jak:
jak:  .
.
W tym wyrażeniu  ,
,

Porównajmy każdy z wyrazów szeregu z podaną dokładnością. Jest oczywiste, że  . Dlatego, aby obliczyć
. Dlatego, aby obliczyć  wystarczy zostawić trzech członków serii.
wystarczy zostawić trzech członków serii.
 lub
lub  .
.
Obliczanie przy użyciu serii znak-dodatnich
Przykład10
.
Oblicz liczbę  z dokładnością 0,001.
z dokładnością 0,001.
Rozwiązanie.
Z rzędu dla funkcji  zastąpić
zastąpić  . Otrzymujemy:
. Otrzymujemy:

Oszacujmy błąd, który powstaje, gdy suma szeregu zostanie zastąpiona sumą pierwszego  członków. Zapiszmy oczywistą nierówność:
członków. Zapiszmy oczywistą nierówność:
tj. 2< <3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
<3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
 ,
, .
.
W zależności od stanu problemu musisz znaleźć n tak, że zachodzi następująca nierówność:  lub
lub  .
.
Łatwo to sprawdzić, kiedy n= 6: .
.
W konsekwencji,  .
.
Przykład11
.
Oblicz  z dokładnością 0,0001.
z dokładnością 0,0001.
Rozwiązanie.
Zauważ, że do obliczenia logarytmów można zastosować szereg dla funkcji  , ale ta seria zbiega się bardzo powoli i trzeba by wziąć 9999 wyrazów, aby osiągnąć daną dokładność! Dlatego do obliczania logarytmów z reguły stosuje się szereg funkcji
, ale ta seria zbiega się bardzo powoli i trzeba by wziąć 9999 wyrazów, aby osiągnąć daną dokładność! Dlatego do obliczania logarytmów z reguły stosuje się szereg funkcji  , który zbiega się w przedziale
, który zbiega się w przedziale  .
.
Obliczać  z tym wierszem. Wynajmować
z tym wierszem. Wynajmować  , następnie
, następnie  .
.
W konsekwencji,  ,
,
Aby obliczyć  z określoną dokładnością weź sumę pierwszych czterech wyrazów:
z określoną dokładnością weź sumę pierwszych czterech wyrazów:  .
.
Reszta rzędu  wyrzucać. Oszacujmy błąd. To oczywiste, że
wyrzucać. Oszacujmy błąd. To oczywiste, że 
lub  .
.

Zatem w szeregu użytym do obliczeń wystarczyło wziąć tylko pierwsze cztery wyrazy zamiast 9999 w szeregu dla funkcji  .
.
Pytania do autodiagnozy
1. Co to jest seria Taylora?
2. jaki rodzaj serii miał Maclaurin?
3. Sformułuj twierdzenie o rozwinięciu funkcji w szereg Taylora.
4. Napisz rozwinięcie głównych funkcji w szereg Maclaurina.
5. Wskaż obszary zbieżności rozpatrywanego szeregu.
6. Jak oszacować błąd w obliczeniach przybliżonych za pomocą szeregów potęgowych?
Jeżeli funkcja f(x) ma pochodne wszystkich rzędów na pewnym przedziale zawierającym punkt a, to można do niej zastosować wzór Taylora:
,
gdzie rn- tzw. człon rezydualny lub reszta szeregu, można go oszacować za pomocą wzoru Lagrange'a:
, gdzie liczba x leży między x i a.
Zasady wprowadzania funkcji:
Jeśli za jakąś wartość X rn→0 w n→∞, to w granicy wzór Taylora zamienia się dla tej wartości na zbieżny Seria Taylora:
,
Zatem funkcja f(x) może być rozszerzona na szereg Taylora w rozważanym punkcie x, jeżeli:
1) posiada instrumenty pochodne wszystkich zleceń;
2) skonstruowany szereg zbiega się w tym miejscu.
Dla a = 0 otrzymujemy szereg o nazwie w pobliżu Maclaurin:
,
Rozbudowa najprostszych (elementarnych) funkcji z serii Maclaurin:
funkcje wykładnicze
, R=∞
Funkcje trygonometryczne ![]() , R=∞
, R=∞ ![]() , R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Funkcja actgx nie rozszerza się w potęgach x, ponieważ ctg0=∞
Funkcje hiperboliczne
Funkcje logarytmiczne
, -1
Szeregi dwumianowe
![]() .
.
Przykład 1. Rozwiń funkcję w szereg mocy f(x)= 2x.
Rozwiązanie. Znajdźmy wartości funkcji i jej pochodne w X=0
f(x) = 2x, f( 0)
= 2 0
=1;
f"(x) = 2x ln2, f"( 0)
= 2 0
ln2=ln2;
f""(x) = 2x w 2 2, f""( 0)
= 2 0
log 2 2= log 2 2;
…
f(n)(x) = 2x ja n 2, f(n)( 0)
= 2 0
ja n 2=ln n 2.
Podstawiając otrzymane wartości pochodnych do wzoru na szereg Taylora, otrzymujemy:
Promień zbieżności tego szeregu jest równy nieskończoności, więc rozwinięcie to obowiązuje dla -∞<x<+∞.
Przykład #2. Napisz szereg Taylora w potęgach ( X+4) dla funkcji f(x)= mi x.
Rozwiązanie. Znajdowanie pochodnych funkcji e x i ich wartości w punkcie X=-4.
f(x)= e x, f(-4)
= e -4
;
f"(x)= e x, f"(-4)
= e -4
;
f""(x)= e x, f""(-4)
= e -4
;
…
f(n)(x)= e x, f(n)( -4)
= e -4
.
Zatem pożądany szereg Taylora funkcji ma postać:
To rozszerzenie obowiązuje również dla -∞<x<+∞.
Przykład #3. Rozwiń funkcję f(x)=ln x w szeregu stopniami ( X- 1),
(tj. w szeregu Taylora w pobliżu punktu X=1).
Rozwiązanie. Znajdujemy pochodne tej funkcji.
f(x)=lnx , , , ,
f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f(n)=(- 1) n-1 (n-1)!
Podstawiając te wartości do wzoru, otrzymujemy pożądaną serię Taylora:
Za pomocą testu d'Alemberta można sprawdzić, czy szereg jest zbieżny przy ½x-1½<1 . Действительно,
Szereg jest zbieżny, jeśli ½ X- 1½<1, т.е. при 0<x<2. При X=2 otrzymujemy szereg przemienny spełniający warunki testu Leibniza. Dla x=0 funkcja nie jest zdefiniowana. Zatem obszar zbieżności szeregu Taylora jest przedziałem półotwartym (0;2]).
Przykład #4. Rozwiń funkcję w serii potęgowej. Przykład nr 5. Rozszerz funkcję w serii Maclaurina. Komentarz
.
Metoda ta opiera się na twierdzeniu o jednoznaczności rozwinięcia funkcji w szereg potęgowy. Istotą tego twierdzenia jest to, że w sąsiedztwie tego samego punktu nie można uzyskać dwóch różnych szeregów potęgowych, które zbiegałyby się do tej samej funkcji, bez względu na sposób jego rozwinięcia. Przykład nr 5a. Rozwiń funkcję w szeregu Maclaurina, wskaż obszar zbieżności. Ułamek 3/(1-3x) może być postrzegany jako suma nieskończenie malejącego postępu geometrycznego o mianowniku 3x, jeśli |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
Przykład nr 6. Rozwiń funkcję w szeregu Taylora w pobliżu punktu x = 3. Przykład numer 7. Napisz szereg Taylora w potęgach (x -1) funkcji ln(x+2) . Przykład numer 8. Rozwiń funkcję f(x)=sin(πx/4) w szeregu Taylora wokół punktu x =2. Przykład 1. Oblicz ln(3) z dokładnością do 0,01. Przykład #2. Oblicz z dokładnością do 0,0001. Przykład #3. Oblicz całkę ∫ 0 1 4 sin (x) x z dokładnością do 10 -5 . Przykład #4. Oblicz całkę ∫ 0 1 4 e x 2 z dokładnością do 0,001. Rozkład funkcji w szeregu Taylora, Maclaurina i Laurenta na stronie w celu szkolenia praktycznych umiejętności. To rozszerzenie serii funkcji daje matematykom pomysł na oszacowanie przybliżonej wartości funkcji w pewnym momencie w jej dziedzinie definicji. O wiele łatwiej jest obliczyć taką wartość funkcji w porównaniu z użyciem przestarzałej w dobie komputeryzacji tablicy Bredisa. Rozwinięcie funkcji w szereg Taylora oznacza obliczenie współczynników przed funkcjami liniowymi tego szeregu i zapisanie ich we właściwej postaci. Uczniowie mylą te dwie serie, nie rozumiejąc, co jest przypadkiem ogólnym, a co szczególnym przypadku drugiego. Przypominamy raz na zawsze, że szereg Maclaurina jest szczególnym przypadkiem szeregu Taylora, czyli jest to szereg Taylora, ale w punkcie x = 0. Wszystkie krótkie zapisy rozwinięcia znanych funkcji, takie jak e ^x, Sin(x), Cos(x) i inne, są to rozwinięcia w szereg Taylora, ale w punkcie 0 dla argumentu. W przypadku funkcji złożonego argumentu szereg Laurenta jest najczęstszym problemem w TFKT, ponieważ reprezentuje dwustronny szereg nieskończony. Jest to suma dwóch wierszy. Sugerujemy zapoznanie się z przykładem dekompozycji bezpośrednio na stronie, bardzo łatwo to zrobić klikając na "Przykład" z dowolnym numerem, a następnie przycisk "Rozwiązanie". Z tym rozwinięciem funkcji w szereg jest związany szereg majoryzacji, który ogranicza pierwotną funkcję w pewnym obszarze wzdłuż osi rzędnych, jeśli zmienna należy do obszaru odciętej. Analiza wektorowa jest porównywana z inną interesującą dyscypliną matematyki. Ponieważ każdy termin wymaga zbadania, proces ten zajmuje dużo czasu. Dowolny szereg Taylora można skojarzyć z szeregiem Maclaurina przez zastąpienie x0 zerem, ale dla szeregu Maclaurina odwrotna reprezentacja szeregu Taylora czasami nie jest oczywista. Bez względu na to, jak nie jest to wymagane w czystej postaci, jest to interesujące dla ogólnego samorozwoju. Każdy szereg Laurenta odpowiada dwustronnemu nieskończonemu szeregowi potęgowemu w potęgach całkowitych z-a, innymi słowy szeregowi tego samego typu Taylora, ale nieco innym w obliczaniu współczynników. O obszarze zbieżności szeregu Laurenta omówimy nieco później, po kilku obliczeniach teoretycznych. Podobnie jak w ubiegłym stuleciu, stopniowe rozwinięcie funkcji w szereg nie może być osiągnięte tylko przez sprowadzenie wyrazów do wspólnego mianownika, ponieważ funkcje w mianownikach są nieliniowe. Przybliżone obliczenie wartości funkcjonalnej wymaga sformułowania problemów. Pomyśl o tym, że gdy argumentem szeregu Taylora jest zmienna liniowa, to rozwinięcie odbywa się w kilku krokach, ale zupełnie inny obraz, gdy funkcja złożona lub nieliniowa działa jako argument funkcji do rozwinięcia, to proces przedstawiania takiej funkcji w szeregu potęgowym jest oczywisty, bo w ten sposób łatwo jest obliczyć, aczkolwiek przybliżoną, ale wartość w dowolnym punkcie dziedziny definicji, z minimalnym błędem, który ma niewielki wpływ na dalsze obliczenia. Dotyczy to również serii Maclaurin. gdy konieczne jest obliczenie funkcji w punkcie zerowym. Jednak sama seria Laurent jest tutaj reprezentowana przez rozszerzenie płaszczyzny z wyimaginowanymi jednostkami. Nie bez powodzenia będzie również prawidłowe rozwiązanie problemu w trakcie całego procesu. W matematyce takie podejście nie jest znane, ale obiektywnie istnieje. W efekcie można dojść do wniosku o tzw. podzbiory punktowe, aw rozwinięciu funkcji w szereg trzeba zastosować znane dla tego procesu metody, takie jak zastosowanie teorii pochodnych. Po raz kolejny jesteśmy przekonani o poprawności nauczyciela, który poczynił swoje założenia dotyczące wyników obliczeń poobliczeniowych. Zauważmy, że szereg Taylora, uzyskany zgodnie ze wszystkimi kanonami matematyki, istnieje i jest zdefiniowany na całej osi liczbowej, jednak drodzy użytkownicy serwisu internetowego, nie zapominajcie o postaci pierwotnej funkcji, bo może się okazać że najpierw trzeba ustalić dziedzinę funkcji, czyli wypisać i wykluczyć z dalszych rozważań te punkty, w których funkcja nie jest zdefiniowana w dziedzinie liczb rzeczywistych. Że tak powiem, to pokaże twoją szybkość w rozwiązaniu problemu. Konstrukcja szeregu Maclaurina z zerową wartością argumentu nie będzie wyjątkiem od tego, co zostało powiedziane. Jednocześnie nikt nie odwołał procesu poszukiwania dziedziny definicji funkcji i do tego matematycznego działania trzeba podejść z całą powagą. Jeśli seria Laurenta zawiera główną część, parametr „a” zostanie nazwany izolowanym punktem osobliwym, a seria Laurenta zostanie rozszerzona w pierścieniu - jest to przecięcie obszarów zbieżności jego części, z których odpowiedni twierdzenie nastąpi. Ale nie wszystko jest tak trudne, jak mogłoby się wydawać niedoświadczonemu uczniowi na pierwszy rzut oka. Po przestudiowaniu tylko szeregu Taylora można łatwo zrozumieć szereg Laurenta - uogólniony przypadek rozszerzania przestrzeni liczb. Jakiekolwiek rozwinięcie funkcji w szereg może być wykonane tylko w punkcie w dziedzinie tej funkcji. Należy wziąć pod uwagę właściwości takich funkcji, na przykład okresowość lub nieskończone różniczkowanie. Sugerujemy również skorzystanie z tabeli gotowych rozwinięć w szereg funkcji elementarnych Taylora, ponieważ jedna funkcja może być reprezentowana przez nawet kilkadziesiąt szeregów potęgowych, które różnią się od siebie, co można zobaczyć korzystając z naszego internetowego kalkulator. Seria online firmy Maclaurin jest łatwiejsza niż kiedykolwiek do ustalenia, czy korzystasz z unikalnej usługi witryny, wystarczy wprowadzić poprawną funkcję pisemną, a otrzymasz prezentowaną odpowiedź w ciągu kilku sekund, będzie ona gwarantowana dokładna i w standardowej formie pisemnej . Możesz natychmiast przepisać wynik w czystej kopii w celu dostarczenia nauczycielowi. Właściwe byłoby najpierw wyznaczenie analityczności rozważanej funkcji w pierścieniach, a następnie jednoznaczne stwierdzenie, że można ją rozszerzyć w szereg Laurenta we wszystkich takich pierścieniach. Ważnym punktem jest, aby nie stracić z oczu członków serii Laurent zawierających stopnie ujemne. Skoncentruj się na tym tak bardzo, jak to możliwe. Zrób dobry użytek z twierdzenia Laurenta o rozwinięciu funkcji w szereg w potęgach całkowitych. W teorii szeregów funkcyjnych centralne miejsce zajmuje dział poświęcony rozwinięciu funkcji w szereg. Powstaje więc problem: dla danej funkcji
wymagane jest znalezienie takiej serii potęgowej która zbiegała się na pewnym przedziale, a jej suma była równa To zadanie nazywa się problem rozwinięcia funkcji w szereg potęgowy. Warunek konieczny do rozwinięcia funkcji w szereg potęgowy jest jego różniczkowalność nieskończoną ilość razy - wynika to z własności zbieżnych szeregów potęgowych. Warunek ten jest z reguły spełniony dla funkcji elementarnych w ich dziedzinie definicji. Załóżmy więc, że funkcja Załóżmy, że funkcja gdzie a 0 ,a 1 ,a 2 ,...,a P ,...
– niepewne (jeszcze) współczynniki. Ustawmy w równości (*) wartość x = x 0 ,
wtedy dostajemy Rozróżniamy szereg potęgowy (*) termin po term i umieszczam tutaj x = x 0 ,
dostajemy Przy kolejnym zróżnicowaniu otrzymujemy serię zarozumiały x = x 0 ,
dostajemy Później P-zróżnicowanie krotnie otrzymujemy Zakładając w ostatniej równości x = x 0 ,
dostajemy Więc współczynniki zostały znalezione zastępując które w wierszu (*), otrzymujemy Powstała seria nazywa się blisko Taylor
dla funkcji
W ten sposób ustaliliśmy, że jeśli funkcja może być rozszerzona na szereg potęgowy w potęgach (x - x 0 ), to rozwinięcie to jest unikatowe, a wynikowy szereg jest z konieczności szeregiem Taylora. Zauważ, że szereg Taylora można otrzymać dla dowolnej funkcji, która ma pochodne dowolnego rzędu w punkcie x = x 0 .
Nie oznacza to jednak, że między funkcją a wynikowym szeregiem można umieścić znak równości, tj. że suma szeregu jest równa pierwotnej funkcji. Po pierwsze taka równość może mieć sens tylko w obszarze zbieżności, a szereg Taylora otrzymany dla funkcji może być rozbieżny, a po drugie, jeśli szereg Taylora jest zbieżny, to jego suma może nie pokrywać się z pierwotną funkcją. Sformułujmy oświadczenie, za pomocą którego zostanie rozwiązany postawiony problem. Jeśli funkcja
gdzieR n (X)- wyraz resztkowy ze wzoru Taylora - ma postać (forma Lagrange'a) gdzie
kropkaξ
leży między x i x 0 . Zauważ, że istnieje różnica między szeregiem Taylora a wzorem Taylora: wzór Taylora jest sumą skończoną, tj. P - stała liczba. Przypomnijmy, że suma szeregu S(x)
można zdefiniować jako granicę funkcjonalnego ciągu sum częściowych S P (x)
w pewnym odstępie czasu X: Zgodnie z tym rozwinięcie funkcji do szeregu Taylora oznacza znalezienie szeregu takiego, że dla dowolnego XX Wzór Taylora zapisujemy w postaci gdzie Zauważ, że Jeśli W ten sposób udowodniliśmy kryterium rozwinięcia funkcji w szereg Taylora.
Aby w pewnym przedziale funkcjaf(x) rozwija się w szereg Taylora, konieczne i wystarczające jest, aby na tym przedziale
Za pomocą sformułowanego kryterium można uzyskać: wystarczającywarunki rozwinięcia funkcji w szereg Taylora.
Jeśli wjakieś sąsiedztwo punktu x 0 wartości bezwzględne wszystkich pochodnych funkcji są ograniczone tą samą liczbą M≥ 0, czyli Z powyższego wynika algorytmrozszerzenie funkcji
f(x) w szeregu Taylora w pobliżu punktu X 0 :
1.
Znajdowanie funkcji pochodnych f(x):
f(x), f’(x), f”(x), f’”(x), f (n) (x),… 2. Obliczamy wartość funkcji i wartości jej pochodnych w punkcie X 0 f(x 0
), f'(x 0
), f”(x 0
), f’”(x 0
), f (n) (x 0
),…
3. Formalnie piszemy szereg Taylora i znajdujemy obszar zbieżności wynikowych szeregów potęgowych. 4. Sprawdzamy spełnienie wystarczających warunków tj. ustalić dla którego X z regionu konwergencji, pozostały termin R n (x)
dąży do zera w Rozwinięcie funkcji w szereg Taylora według tego algorytmu nazywa się rozwinięcie funkcji w szereg Taylora z definicji lub bezpośredni rozkład. Wśród serii funkcjonalnych najważniejsze miejsce zajmują serie potęgowe. Seria potęg nazywana jest serią których członkami są funkcje potęgowe ułożone w rosnące nieujemne potęgi całkowite x, a c0
, c 1
, c 2
, c n
są wartościami stałymi. Liczby c1
, c 2
, c n
- współczynniki członków serii, c0
- Wolny Członek. Terminy szeregu potęgowego są zdefiniowane na całej osi liczbowej. Zapoznajmy się z koncepcją obszar zbieżności szeregu potęgowego.
To jest zbiór wartości zmiennych x dla których szereg jest zbieżny. Szeregi potęgowe mają dość prosty obszar zbieżności. Dla rzeczywistych wartości zmiennej x obszar zbieżności składa się albo z jednego punktu, albo stanowi pewien przedział (przedział zbieżności) lub pokrywa się z całą osią Wół
. Podczas podstawienia w szereg potęgowy, wartości x= 0 otrzymujesz serię liczb c0
+0+0+...+0+...
, który zbiega się. Dlatego w x= 0 zbiega dowolny szereg potęgowy, a zatem obszar konwergencji
nie może być zbiorem pustym. Struktura obszaru zbieżności wszystkich szeregów potęgowych jest taka sama. Można to ustalić za pomocą następującego twierdzenia. Twierdzenie 1 (twierdzenie Abela). Jeśli szereg potęgowy zbiega się przy pewnej wartości x = x 0
, który jest różny od zera, to jest zbieżny, a ponadto absolutnie dla wszystkich wartości |x| < |x 0
|
. Uwaga: zarówno wartość początkowa „x to zero”, jak i każda wartość „x”, która jest porównywana z wartością początkową, są przyjmowane modulo - bez uwzględniania znaku. Konsekwencja. Jeśli szeregi mocy są rozbieżne
w jakiejś wartości x = x 1
, to rozbiega się dla wszystkich wartości |x| > |x 1
|
. Jak dowiedzieliśmy się wcześniej, każdy szereg potęgowy jest zbieżny dla wartości x= 0. Istnieją szeregi potęgowe, które są zbieżne tylko dla x= 0 i rozchodzą się dla innych wartości X. Wyłączając ten przypadek z rozważań, zakładamy, że szereg potęgowy jest zbieżny przy pewnej wartości x = x 0
, różne od zera. Następnie, zgodnie z twierdzeniem Abela, zbiega się we wszystkich punktach przedziału ]-| x0
|, |x 0
|[
(przedział, którego lewa i prawa granica są wartościami x, przy których szereg potęgowy jest zbieżny, przyjmowany odpowiednio ze znakiem minus i ze znakiem plus), symetryczny względem początku. Jeśli szereg potęgowy rozbiega się o pewną wartość x = x 1
, a następnie, w oparciu o wniosek z twierdzenia Abela, rozchodzi się również we wszystkich punktach poza segmentem [-| x1
|, |x 1
|]
. Wynika z tego, że dla każdego szeregu potęgowego istnieje symetryczny względem początku przedział , zwany przedział zbieżności
, w każdym punkcie, w którym szereg jest zbieżny, może zbiegać się na granicach lub może się rozbiegać i niekoniecznie jednocześnie, ale poza segmentem, szereg rozchodzi się. Numer R nazywa się promieniem zbieżności szeregu potęgowego. W szczególnych przypadkach przedział zbieżności szeregów potęgowych
może zdegenerować się do punktu (wtedy szereg jest zbieżny tylko dla x= 0 i przyjmuje się, że R= 0) lub reprezentują całą oś liczbową (wtedy szereg zbiega się we wszystkich punktach osi liczbowej i zakłada się, że ). Zatem definicja obszaru zbieżności szeregu potęgowego ma na celu określenie jego promień zbieżności
R oraz badanie zbieżności szeregu na granicach przedziału zbieżności (dla ). Twierdzenie 2. Jeżeli wszystkie współczynniki szeregu potęgowego, zaczynając od pewnego, są niezerowe, to jego promień zbieżności jest równy granicy w stosunku wartości bezwzględnych współczynników ogólnych następujących członków szeregu, tj. Przykład 1. Znajdź obszar zbieżności szeregu potęgowego Rozwiązanie. Tutaj Korzystając ze wzoru (28), znajdujemy promień zbieżności tego szeregu: Zbadajmy zbieżność szeregu na końcach przedziału zbieżności . Przykład 13 pokazuje, że szereg ten jest zbieżny dla x= 1 i odbiega w x= -1. Dlatego regionem zbieżności jest półprzedział . Przykład 2. Znajdź obszar zbieżności szeregu potęgowego Rozwiązanie. Współczynniki szeregu są dodatnie i Znajdźmy granicę tego stosunku, tj. promień zbieżności szeregów potęgowych: Badamy zbieżność szeregu na końcach przedziału . Substytucja wartości x= -1/5 i x= 1/5 w tej serii daje: Pierwsza z tych serii jest zbieżna (patrz przykład 5). Ale wtedy, na mocy twierdzenia z paragrafu „Zbieżność absolutna”, druga seria również jest zbieżna, a obszarem jej zbieżności jest odcinek Przykład 3. Znajdź obszar zbieżności szeregu potęgowego Rozwiązanie. Tutaj Korzystając ze wzoru (28), znajdujemy promień zbieżności szeregu: Przeanalizujmy zbieżność szeregu dla wartości. Zastępując je odpowiednio w tej serii otrzymujemy Oba szeregi są rozbieżne, ponieważ konieczny warunek zbieżności nie jest spełniony (ich wspólne terminy nie mają tendencji do zerowania w ). Tak więc na obu końcach przedziału zbieżności szereg ten jest rozbieżny, a obszarem jego zbieżności jest przedział . Przykład 5. Znajdź obszar zbieżności szeregu potęgowego Rozwiązanie. Znajdujemy relację , gdzie , i Zgodnie ze wzorem (28) promień zbieżności tego szeregu czyli szereg zbiega się tylko wtedy, gdy x= 0 i rozbiega się dla innych wartości X. Przykłady pokazują, że szeregi zachowują się inaczej na końcach przedziału zbieżności. W przykładzie 1 szereg zbiega się na jednym końcu przedziału zbieżności i rozbiega się na drugim, w przykładzie 2 zbiega się na obu końcach, w przykładzie 3 rozbiega się na obu końcach. Wzór na promień zbieżności szeregu potęgowego otrzymuje się przy założeniu, że wszystkie współczynniki wyrazów szeregu, począwszy od niektórych, są niezerowe. Dlatego stosowanie wzoru (28) jest dopuszczalne tylko w tych przypadkach. W przypadku naruszenia tego warunku promień zbieżności szeregu potęgowego należy szukać za pomocą znak d'Alembert lub, dokonując zmiany zmiennej, przekształcając szereg do postaci, w której spełniony jest określony warunek. Przykład 6. Znajdź przedział zbieżności szeregu potęgowego Rozwiązanie. Ta seria nie zawiera terminów z nieparzystymi stopniami X. Dlatego przekształcamy serię, ustawiając . Następnie otrzymujemy serię Wzór (28) może być wykorzystany do znalezienia promienia zbieżności którego. Ponieważ , i , to promień zbieżności tego szeregu Z równości otrzymujemy zatem szereg ten zbiega się na przedziale . Niech dla serii mocy promień zbieżności R> 0, tj. seria ta zbiega się w przedziale . Następnie każda wartość X z przedziału zbieżności odpowiada pewna suma szeregu. Dlatego suma szeregu potęgowego jest funkcją X na przedziale zbieżności. Oznaczając to przez f(x), możemy napisać równość rozumiejąc to w tym sensie, że suma szeregu w każdym punkcie X z przedziału zbieżności jest równa wartości funkcji f(x) w tym momencie. W tym samym sensie powiemy, że szereg potęgowy (29) jest zbieżny do funkcji f(x) na przedziale zbieżności. Poza przedziałem zbieżności równość (30) nie ma znaczenia. Przykład 7 Znajdź sumę szeregu potęgowego Rozwiązanie. To jest seria geometryczna a= 1 i q= x. Dlatego jego suma jest funkcją ważne tylko dla wartości, chociaż funkcja Można wykazać, że suma szeregu potęgowego f(x) jest ciągła i różniczkowalna na dowolnym przedziale w przedziale zbieżności, w szczególności w dowolnym punkcie przedziału zbieżności szeregu. Przedstawmy twierdzenia dotyczące różniczkowania wyraz po wyrazie i całkowania szeregów potęgowych. Twierdzenie 1. Szereg potęgowy (30) w przedziale jego zbieżności można różniczkować członowo nieograniczoną liczbę razy, a wynikowy szereg potęgowy ma taki sam promień zbieżności jak szereg pierwotny, a ich sumy są odpowiednio równe . Twierdzenie 2. Szereg potęgowy (30) może być całkowany term po term nieograniczoną liczbę razy w zakresie od 0 do X, if , a wynikowe szeregi potęgowe mają taki sam promień zbieżności jak szereg pierwotny, a ich sumy są odpowiednio równe Niech funkcja f(x), który ma zostać rozszerzony w szereg potęgowy, tj. reprezentować w formularzu (30): Problem polega na określeniu współczynników ……………………………………………….. (31) Zakładając w równości (30) i (31) X= 0, znajdujemy Podstawiając znalezione wyrażenia do równości (30), otrzymujemy Znajdźmy rozwinięcie szeregu Maclaurina niektórych funkcji elementarnych. Przykład 8 Rozszerz funkcję w serii Maclaurin Rozwiązanie. Pochodne tej funkcji są takie same jak samej funkcji: Dlatego kiedy X= 0 mamy Podstawiając te wartości do wzoru (32), otrzymujemy pożądaną ekspansję: Seria ta zbiega się na całej osi liczbowej (jej promień zbieżności wynosi ).
Rozwiązanie. W rozkładzie (1) zastępujemy x przez -x 2, otrzymujemy:
, -∞
Rozwiązanie. Mamy
Korzystając ze wzoru (4) możemy napisać:
zastępując zamiast x we wzorze -x, otrzymujemy:
Stąd znajdujemy: ln(1+x)-ln(1-x) = -
Rozszerzając nawiasy, przestawiając terminy serii i dokonując redukcji podobnych terminów, otrzymujemy
. Szereg ten jest zbieżny w przedziale (-1;1), ponieważ jest otrzymywany z dwóch szeregów, z których każdy jest zbieżny w tym przedziale.
Wzory (1)-(5) można również wykorzystać do rozwinięcia odpowiednich funkcji w szereg Taylora, tj. dla rozwinięcia funkcji w dodatnich potęgach całkowitych ( Ha). W tym celu konieczne jest wykonanie takich identycznych przekształceń na danej funkcji w celu uzyskania jednej z funkcji (1) - (5), w której zamiast X koszty k( Ha) m , gdzie k jest liczbą stałą, m jest dodatnią liczbą całkowitą. Często wygodnie jest zmienić zmienną t=Ha i rozwiń otrzymaną funkcję względem t w szeregu Maclaurina.
Rozwiązanie. Najpierw znajdujemy 1-x-6x 2 =(1-3x)(1+2x) , .
do elementarnych:
z obszarem zbieżności |x|< 1/3.
Rozwiązanie. Problem ten można rozwiązać, podobnie jak poprzednio, posługując się definicją szeregu Taylora, dla której konieczne jest znalezienie pochodnych funkcji i ich wartości przy X=3. Łatwiej będzie jednak wykorzystać istniejącą dekompozycję (5):
=
Powstały szereg jest zbieżny przy lub -3
Rozwiązanie.
Szereg zbiega się przy , czyli -2< x < 5.
Rozwiązanie. Zróbmy zamianę t=x-2:
Korzystając z rozwinięcia (3), w którym podstawiamy π / 4 t za x, otrzymujemy:
Wynikowy szereg jest zbieżny do danej funkcji w -∞< π / 4 t<+∞, т.е. при (-∞
, (-∞Przybliżone obliczenia z wykorzystaniem szeregów potęgowych
Szeregi potęgowe są szeroko stosowane w obliczeniach przybliżonych. Za ich pomocą z określoną dokładnością można obliczyć wartości pierwiastków, funkcje trygonometryczne, logarytmy liczb, całki oznaczone. Szeregi są również wykorzystywane do całkowania równań różniczkowych.
Rozważ rozwinięcie funkcji w szereg potęgowy:
Aby obliczyć przybliżoną wartość funkcji w danym punkcie X, należący do obszaru zbieżności wskazanego szeregu, pierwszy n członkowie ( n jest liczbą skończoną), a pozostałe terminy są odrzucane:
Aby oszacować błąd uzyskanej przybliżonej wartości, konieczne jest oszacowanie odrzuconej reszty r n (x) . W tym celu stosuje się następujące metody:
Rozwiązanie. Użyjmy dekompozycji , gdzie x=1/2 (patrz przykład 5 w poprzednim temacie):
Sprawdźmy, czy możemy odrzucić resztę po pierwszych trzech składnikach rozwinięcia, w tym celu obliczamy ją za pomocą sumy nieskończenie malejącego postępu geometrycznego:
Więc możemy odrzucić tę resztę i uzyskać
Rozwiązanie. Użyjmy szeregu dwumianowego. Ponieważ 5 3 jest najbliższą liczbą całkowitą sześcianem 130, zaleca się reprezentowanie liczby 130 jako 130=5 3 +5. 
ponieważ czwarty wyraz otrzymanego szeregu przemiennego znakowego, który spełnia test Leibniza, jest już mniejszy niż wymagana dokładność:
, więc można go odrzucić i następujące po nim terminy.
Wiele praktycznie niezbędnych całek oznaczonych lub niewłaściwych nie można obliczyć za pomocą wzoru Newtona-Leibniza, ponieważ jego zastosowanie wiąże się ze znalezieniem funkcji pierwotnej, często nie mającej wyrażenia w funkcjach elementarnych. Zdarza się również, że znalezienie funkcji pierwotnej jest możliwe, ale niepotrzebnie pracochłonne. Jeżeli jednak całka jest rozszerzona na szereg potęgowy, a granice całkowania należą do przedziału zbieżności tego szeregu, to możliwe jest przybliżone obliczenie całki z zadaną dokładnością.
Rozwiązanie. Odpowiednia całka nieoznaczona nie może być wyrażona w funkcjach elementarnych, tj. jest „całką niemożliwą”. Nie można tutaj zastosować wzoru Newtona-Leibniza. Obliczmy całkę w przybliżeniu.
Dzielenie wyrazu przez wyraz szeregu dla grzechu x na x otrzymujemy: 
Całkując ten szereg wyraz po wyrazie (jest to możliwe, ponieważ granice całkowania należą do przedziału zbieżności tego szeregu), otrzymujemy:
Ponieważ otrzymany szereg spełnia warunki Leibniza i wystarczy wziąć sumę dwóch pierwszych wyrazów, aby z zadaną dokładnością otrzymać żądaną wartość.
W ten sposób znajdujemy  .
.
Rozwiązanie.

![]() . Sprawdźmy, czy możemy odrzucić resztę po drugim członie szeregu wynikowego.
. Sprawdźmy, czy możemy odrzucić resztę po drugim członie szeregu wynikowego.
0,0001<0.001. Следовательно,  .
. ,
tych.
,
tych. =
..
=
..
 ma pochodne dowolnego zamówienia. Czy można go rozszerzyć do serii potęgowej, jeśli tak, to jak znaleźć tę serię? Druga część problemu jest łatwiejsza do rozwiązania, więc zacznijmy od niej.
ma pochodne dowolnego zamówienia. Czy można go rozszerzyć do serii potęgowej, jeśli tak, to jak znaleźć tę serię? Druga część problemu jest łatwiejsza do rozwiązania, więc zacznijmy od niej. można przedstawić jako sumę szeregu potęgowego zbieżnego w przedziale zawierającym punkt X 0 :
można przedstawić jako sumę szeregu potęgowego zbieżnego w przedziale zawierającym punkt X 0 :
 =
..
(*)
=
..
(*) .
. =
..
=
..
 .
. =
..
=
..
 , gdzie
, gdzie  .
. , gdzie
, gdzie
 ,
,
 ,
,
 ,
…,
,
…,
 ,….,
,…., .
.
3.2. Warunki dostateczne rozwinięcia funkcji w szereg Taylora
 w jakimś sąsiedztwie punktu x 0 ma instrumenty pochodne do (n+
1)-ty rząd włącznie, to w tej okolicy mamyformuła
Taylor
w jakimś sąsiedztwie punktu x 0 ma instrumenty pochodne do (n+
1)-ty rząd włącznie, to w tej okolicy mamyformuła
Taylor

 .
.
 definiuje otrzymany błąd, zamień funkcję f(x)
wielomian S n (x).
definiuje otrzymany błąd, zamień funkcję f(x)
wielomian S n (x).
 , następnie
, następnie  ,tych. funkcja rozwija się w szereg Taylora. I odwrotnie, jeśli
,tych. funkcja rozwija się w szereg Taylora. I odwrotnie, jeśli  , następnie
, następnie  .
. , gdzieR n (x) to pozostała część szeregu Taylora.
, gdzieR n (x) to pozostała część szeregu Taylora. , to w tym sąsiedztwie funkcja rozwija się w szereg Taylora.
, to w tym sąsiedztwie funkcja rozwija się w szereg Taylora. lub
lub
 .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]() :
:![]()
![]() ,
,![]()
![]()
![]()
Suma szeregów potęgowych. Różniczkowanie i całkowanie szeregów mocy
![]()
![]() . Szereg jest zbieżny jeśli , i jest jego przedziałem zbieżności. Dlatego równość
. Szereg jest zbieżny jeśli , i jest jego przedziałem zbieżności. Dlatego równość![]()
![]() zdefiniowany dla wszystkich wartości X, Oprócz X= 1.
zdefiniowany dla wszystkich wartości X, Oprócz X= 1.
Rozszerzenie funkcji w szeregi potęgowe
![]() rząd (30). Aby to zrobić, różnicując równość (30) termin po terminie, kolejno znajdujemy:
rząd (30). Aby to zrobić, różnicując równość (30) termin po terminie, kolejno znajdujemy:![]()
![]()
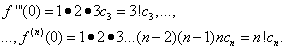
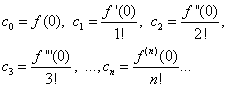
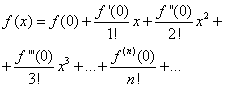 (32)
(32)
![]() (33)
(33)

