wartość przyrodnicza. Liczby naturalne - podstawy
Liczby to pojęcie abstrakcyjne. Są ilościową charakterystyką obiektów i są rzeczywiste, racjonalne, ujemne, całkowite i ułamkowe, a także naturalne.
W liczeniach stosuje się zwykle szeregi naturalne, w których w sposób naturalny powstają oznaczenia ilościowe. Znajomość konta zaczyna się we wczesnym dzieciństwie. Który dzieciak uniknął zabawnych wyliczanek, w których wykorzystano właśnie elementy naturalnego liczenia? "Raz, dwa, trzy, cztery, pięć ... Króliczek wyszedł na spacer!" lub "1, 2, 3, 4, 5, 6, 7, 8, 9, 10, król postanowił mnie powiesić..."
Dla dowolnej liczby naturalnej możesz znaleźć inną, większą od niej. Ten zbiór jest zwykle oznaczony literą N i powinien być uważany za nieskończony w kierunku wzrostu. Ale ten zestaw ma początek - to jest jednostka. Chociaż istnieją francuskie liczby naturalne, których zbiór zawiera również zero. Ale głównym wyróżnikiem obu zbiorów jest fakt, że nie zawierają one ani liczb ułamkowych, ani ujemnych.
Potrzeba liczenia różnych przedmiotów pojawiła się w czasach prehistorycznych. Wtedy rzekomo powstało pojęcie „liczb naturalnych”. Jego powstanie miało miejsce podczas całego procesu zmiany światopoglądu człowieka, rozwoju nauki i technologii.
Jednak nie potrafili jeszcze myśleć abstrakcyjnie. Trudno im było zrozumieć, co łączy pojęcia „trzech myśliwych” czy „trzech drzew”. Dlatego przy wskazaniu liczby osób zastosowano jedną definicję, a przy wskazaniu tej samej liczby obiektów innego rodzaju posłużono się zupełnie inną definicją.
I był niezwykle krótki. Były w nim tylko liczby 1 i 2, a liczenie zakończyło się pojęciem „wiele”, „stado”, „tłum”, „góra”.
Później powstała bardziej postępowa relacja, już szersza. Ciekawostką jest to, że były tylko dwie liczby - 1 i 2, a kolejne liczby uzyskano już przez dodanie.
Przykładem tego są informacje, które dotarły do nas o seriach liczbowych plemienia australijskiego, które 1 oznaczały słowo „Enza”, a 2 – słowo „petcheval”. Liczba 3 brzmiała więc jak „petcheval-enza”, a 4 – już jak „petcheval-petcheval”.
Większość narodów uznała palce za standard liczenia. Co więcej, rozwój abstrakcyjnej koncepcji „liczb naturalnych” przebiegał zgodnie z ścieżką używania nacięć na patyku. A potem pojawiła się potrzeba oznaczenia tuzina innym znakiem. Starożytni ludzie, wychodząc, zaczęli używać innego kija, na którym zrobiono nacięcia wskazujące dziesiątki.
Możliwości odtwarzania liczb ogromnie rozszerzyły się wraz z pojawieniem się pisma. Początkowo liczby przedstawiano jako kreski na glinianych tabliczkach lub papirusie, ale stopniowo do pisania zaczęto używać innych znaków, tak pojawiły się cyfry rzymskie.
Znacznie później pojawił się, co otworzyło możliwość pisania liczb za pomocą stosunkowo małego zestawu znaków. Dziś nietrudno zapisać tak ogromne liczby, jak odległość między planetami i liczba gwiazd. Trzeba tylko nauczyć się posługiwać stopniami.
Euklides w III wieku pne w księdze „Początki" ustala nieskończoność zbioru liczbowego. A Archimedes w „Psamicie" ujawnia zasady konstruowania nazw dowolnie dużych liczb. Niemal do połowy XIX wieku ludzie nie stawali przed koniecznością jasnego sformułowania pojęcia „liczby naturalne”. Definicja była wymagana wraz z pojawieniem się aksjomatycznej metody matematycznej.
A w latach 70. XIX wieku sformułował jasną definicję liczb naturalnych w oparciu o koncepcję zbioru. A dzisiaj już wiemy, że liczby naturalne to wszystkie liczby całkowite, od 1 do nieskończoności. Małe dzieci, robiąc pierwszy krok w poznawaniu królowej wszystkich nauk – matematyki – zaczynają studiować te liczby.
1.1 Definicja
Liczby, których ludzie używają podczas liczenia, nazywają się naturalny(na przykład jeden, dwa, trzy, ..., sto, sto jeden, ..., trzy tysiące dwieście dwadzieścia jeden, ...) Do pisania liczb naturalnych używa się znaków specjalnych (symboli) , nazywa figury.
Obecnie akceptowane Notacja dziesiętna. System dziesiętny (lub sposób) pisania liczb wykorzystuje cyfry arabskie. Oto dziesięć różnych cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 .
Najmniej liczba naturalna to liczba jeden, to zapisany cyfrą dziesiętną - 1. Kolejną liczbę naturalną uzyskuje się z poprzedniej (poza jedną) przez dodanie 1 (jeden). To dodawanie można wykonać wielokrotnie (nieskończoną liczbę razy). To znaczy, że Nie największy Liczba naturalna. Dlatego mówi się, że ciąg liczb naturalnych jest nieograniczony lub nieskończony, ponieważ nie ma końca. Liczby naturalne są zapisywane za pomocą cyfr dziesiętnych.
1.2. Liczba „zero”
Aby wskazać brak czegoś, użyj numeru „ zero" lub " zero".
Jest napisany cyframi. 0 (zero).
Na przykład w pudełku wszystkie kule są czerwone. Ile z nich jest zielonych? - Odpowiedź: zero .
Więc w pudełku nie ma zielonych kulek! Liczba 0 może oznaczać, że coś się skończyło. Na przykład Masza miała 3 jabłka. Dzieliła się dwoma z przyjaciółmi, jedną zjadła sama. Więc odeszła 0
(zero) jabłka, tj. nic nie pozostało. Liczba 0 może oznaczać, że coś się nie wydarzyło. Na przykład mecz hokejowy między drużyną rosyjską a drużyną kanadyjską zakończył się wynikiem 3:0
(czytaj „trzy - zero”) na korzyść drużyny rosyjskiej. Oznacza to, że drużyna rosyjska strzeliła 3 gole, a kanadyjska 0 goli, nie mogła strzelić ani jednego gola. Musimy pamiętać że zero nie jest liczbą naturalną.
1.3. Zapisywanie liczb naturalnych
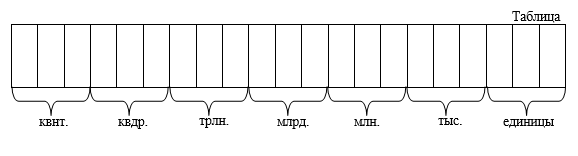
W dziesiętnym sposobie zapisywania liczby naturalnej każda cyfra może oznaczać różne liczby. Zależy to od miejsca tej cyfry w zapisie liczby. Pewne miejsce w zapisie liczby naturalnej nazywa się pozycja. Dlatego zapis dziesiętny nazywa się pozycyjny. Rozważmy zapis dziesiętny 7777 liczby siedem tysięcy siedemset siedemdziesiąt siedem. W tym wpisie jest siedem tysięcy siedemset siedem dziesiątek i siedem jednostek.
Każde z miejsc (pozycji) w zapisie dziesiętnym liczby nazywa się wypisać. Co trzy cyfry są łączone w Klasa. To połączenie jest wykonywane od prawej do lewej (od końca wpisu numeru). Różne stopnie i klasy mają swoje własne nazwy. Liczba liczb naturalnych jest nieograniczona. Dlatego liczba stopni i klas również nie jest ograniczona ( bez końca). Rozważ nazwy cyfr i klas na przykładzie liczby z zapisem dziesiętnym
38 001 102 987 000 128 425:
|
Klasy i stopnie |
||
|
kwintyliony |
setki kwintylionów |
|
|
dziesiątki kwintylionów |
||
|
kwintyliony |
||
|
kwadrylionów |
setki biliardów |
|
|
dziesiątki biliardów |
||
|
kwadrylionów |
||
|
biliony |
setki bilionów |
|
|
dziesiątki bilionów |
||
|
biliony |
||
|
miliardy |
setki miliardów |
|
|
dziesiątki miliardów |
||
|
miliardy |
||
|
miliony |
setki milionów |
|
|
dziesiątki milionów |
||
|
miliony |
||
|
setki tysięcy |
||
|
dziesiątki tysięcy |
||
Tak więc klasy, zaczynając od najmłodszych, mają nazwy: jednostki, tysiące, miliony, miliardy, biliony, kwadrylionów, kwintyliony.
1.4. Jednostki bitowe
Każda z klas w zapisie liczb naturalnych składa się z trzech cyfr. Każda ranga ma jednostki bitowe. Następujące liczby nazywane są jednostkami bitowymi:
1 - cyfrowa jednostka cyfry jednostek,
10 - cyfrowa jednostka cyfry dziesiątek,
100 - bitowa jednostka cyfry setek,
1 000 - bitowa jednostka tysięcy miejsc,
10 000 - cyfrowa jednostka dziesiątek tysięcy,
100 000 - bitowa jednostka setek tysięcy,
1 000 000 to cyfrowa jednostka cyfry milionów itd.
Liczba w dowolnej cyfrze pokazuje liczbę jednostek tej cyfry. Tak więc liczba 9 na miejscu setek miliardów oznacza, że liczba 38 001 102 987 000 128 425 obejmuje dziewięć miliardów (czyli 9 razy 1 000 000 000 lub 9 bitowych jednostek miliardów). Pusta cyfra setek kwintylionów oznacza, że w tej liczbie nie ma setek kwintylionów lub ich liczba jest równa zeru. W takim przypadku liczbę 38 001 102 987 000 128 425 można zapisać w następujący sposób: 038 001 102 987 000 128 425.
Można to zapisać inaczej: 000 038 001 102 987 000 128 425. Zera na początku liczby oznaczają puste cyfry wyższego rzędu. Zwykle nie są zapisywane, w przeciwieństwie do zer w notacji dziesiętnej, które koniecznie oznaczają puste cyfry. A więc trzy zera w klasie milionów oznaczają, że cyfry setek milionów, dziesiątek milionów i jednostek milionów są puste.
1.5. Skróty w zapisie liczb
Podczas pisania liczb naturalnych używa się skrótów. Oto kilka przykładów:
1000 = 1 tysiąc (jeden tysiąc)
23 000 000 = 23 miliony (dwadzieścia trzy miliony)
5 000 000 000 = 5 miliardów (pięć miliardów)
203 000 000 000 000 = 203 bilionów (dwieście trzy biliony)
107 000 000 000 000 000 = 107 mkw. (sto siedem biliardów)
1 000 000 000 000 000 000 = 1 kw. (jeden trylion)
Blok 1.1. Słownik
Opracuj słowniczek nowych terminów i definicji z §1. W tym celu w pustych komórkach wpisz słowa z poniższej listy terminów. W tabeli (na końcu bloku) dla każdej definicji wskaż numer terminu z listy.
Blok 1.2. Samodzielny trening
W świecie wielkich liczb
Gospodarka .
- Budżet Rosji na przyszły rok wyniesie: 6328251684128 rubli.
- Planowane wydatki na ten rok: 5124983252134 rubli.
- Dochody kraju przekroczyły wydatki o 1203268431094 rubli.
Pytania i zadania
- Przeczytaj wszystkie trzy podane liczby
- Wpisz cyfry w klasie milionów każdej z trzech liczb
- Która sekcja w każdej z liczb należy do cyfry na siódmej pozycji od końca zapisu liczb?
- Jaką liczbę jednostek bitowych pokazuje liczba 2 w pierwszej liczbie?... w drugiej i trzeciej liczbie?
- Nazwij jednostkę bitową dla ósmej pozycji od końca w zapisie trzech liczb.
Geografia (długość)
- Promień równikowy Ziemi: 6378245 m
- Obwód równika: 40075696 m
- Największa głębokość oceanu światowego (Rów Maryjny na Pacyfiku) 11500 m
Pytania i zadania
- Przelicz wszystkie trzy wartościna centymetry i odczytaj otrzymane liczby.
- Dla pierwszej liczby (w cm) zapisz liczby w sekcjach:
setki tysięcy _______
dziesiątki milionów _______
tysiące _______
miliardy _______
setki milionów _______
- Dla drugiej liczby (w cm) zapisz jednostki bitowe odpowiadające liczbom 4, 7, 5, 9 we wpisie liczby
- Konwertuj trzecią wartość na milimetry, odczytaj wynikową liczbę.
- Dla wszystkich pozycji w ewidencji trzeciej liczby (w mm) należy wskazać cyfry i jednostki cyfr w tabeli:
Geografia (kwadrat)
- Powierzchnia całej powierzchni Ziemi wynosi 510 083 tysięcy kilometrów kwadratowych.
- Powierzchnia sum na Ziemi wynosi 148 628 tysięcy kilometrów kwadratowych.
- Powierzchnia lustra wody Ziemi wynosi 361.455 tysięcy kilometrów kwadratowych.
Pytania i zadania
- Przekształć wszystkie trzy wartości na metry kwadratowe i odczytaj otrzymane liczby.
- Nazwij klasy i rangi odpowiadające cyfrom niezerowym w zapisie tych liczb (w mkw.).
- We wpisie trzeciej liczby (w m kw.) nazwij jednostki bitowe odpowiadające liczbom 1, 3, 4, 6.
- W dwóch wpisach drugiej wartości (w km kw. i m kw.) wskaż, do których cyfr należy numer 2.
- Zapisz jednostki bitowe dla liczby 2 w rekordach drugiej wartości.
Blok 1.3. Dialog z komputerem.
Wiadomo, że w astronomii często wykorzystuje się duże liczby. Podajmy przykłady. Średnia odległość Księżyca od Ziemi wynosi 384 tys. km. Odległość Ziemi od Słońca (średnia) to 149504 tys. km, Ziemia od Marsa to 55 mln km. Na komputerze za pomocą edytora tekstu Word utwórz tabele tak, aby każda cyfra w rekordzie wskazanych liczb znajdowała się w osobnej komórce (komórce). W tym celu wykonaj polecenia na pasku narzędzi: tabela → dodaj tabelę → liczba wierszy (wstaw kursorem cyfrę „1”) → liczba kolumn (oblicz sam). Utwórz tabele dla innych numerów (blok "Własne przygotowanie").
Blok 1.4. Sztafeta wielkich liczb
Pierwszy wiersz tabeli zawiera dużą liczbę. Przeczytaj to. Następnie wykonaj zadania: przesuwając cyfry we wpisie liczbowym w prawo lub w lewo, zdobądź kolejne cyfry i przeczytaj je. (Nie przesuwaj zer na końcu numeru!). Na zajęciach pałeczkę można przeprowadzić podając ją sobie nawzajem.
Linia 2 . Przenieś wszystkie cyfry numeru w pierwszym wierszu w lewo przez dwie komórki. Zastąp cyfry 5 kolejnym numerem. Wypełnij puste komórki zerami. Przeczytaj numer.
Linia 3 . Przenieś wszystkie cyfry numeru w drugim wierszu w prawo przez trzy komórki. Zastąp liczby 3 i 4 we wpisie liczby następującymi liczbami. Wypełnij puste komórki zerami. Przeczytaj numer.
Linia 4. Przenieś wszystkie cyfry numeru w wierszu 3 o jedną komórkę w lewo. Zmień liczbę 6 w klasie bilionów na poprzednią, a w klasie miliard na następną. Wypełnij puste komórki zerami. Przeczytaj wynikowy numer.
Linia 5 . Przesuń wszystkie cyfry liczby w wierszu 4 o jedną komórkę w prawo. Zastąp liczbę 7 w miejscu „dziesiątki tysięcy” poprzednią, a w miejscu „dziesiątki milionów” kolejną. Przeczytaj wynikowy numer.
Linia 6 . Przenieś wszystkie cyfry liczby w wierszu 5 w lewo po 3 komórkach. Zmień liczbę 8 w setkach miliardów na poprzednią, a 6 w setkach milionów na kolejną liczbę. Wypełnij puste komórki zerami. Oblicz wynikową liczbę.
Linia 7 . Przesuń wszystkie cyfry liczby w wierszu 6 w prawo o jedną komórkę. Zamień cyfry w dziesiątkach biliardów i dziesiątkach miliardów miejsc. Przeczytaj wynikowy numer.
Linia 8 . Przenieś wszystkie cyfry numeru w wierszu 7 w lewo przez jedną komórkę. Zamień cyfry w kwintylionach i kwadrylionach. Wypełnij puste komórki zerami. Przeczytaj wynikowy numer.
Linia 9 . Przenieś wszystkie cyfry liczby w wierszu 8 w prawo przez trzy komórki. Zamień dwie sąsiednie liczby w rzędzie liczb z klas milionów i bilionów. Przeczytaj wynikowy numer.
Linia 10 . Przenieś wszystkie cyfry numeru w wierszu 9 o jedną komórkę w prawo. Przeczytaj wynikowy numer. Zaznacz liczby wskazujące rok olimpiady w Moskwie.
Blok 1.5. Zagrajmy
Rozpalić ogień
Pole gry to obraz choinki. Posiada 24 żarówki. Ale tylko 12 z nich jest podłączonych do sieci energetycznej. Aby wybrać podłączone lampy, należy poprawnie odpowiedzieć na pytania słowami „Tak” lub „Nie”. W tę samą grę można grać na komputerze, poprawna odpowiedź „zapala” żarówkę.
- Czy to prawda, że liczby są specjalnymi znakami do zapisywania liczb naturalnych? (1 - tak, 2 - nie)
- Czy to prawda, że 0 jest najmniejszą liczbą naturalną? (3 - tak, 4 - nie)
- Czy to prawda, że w systemie liczb pozycyjnych ta sama cyfra może oznaczać różne liczby? (5 - tak, 6 - nie)
- Czy to prawda, że pewne miejsce w dziesiętnym zapisie liczb nazywa się miejscem? (7 - tak, 8 - nie)
- Biorąc pod uwagę liczbę 543 384. Czy to prawda, że liczba najbardziej znaczących cyfr to 543, a najmniejsza 384? (9 - tak, 10 - nie)
- Czy to prawda, że w klasie miliardów najstarsza z jednostek bitowych to sto miliardów, a najmłodsza to miliard? (11 - tak, 12 - nie)
- Podano liczbę 458 121. Czy to prawda, że suma cyfr najbardziej znaczących i cyfr najmniej znaczących wynosi 5? (13 - tak, 14 - nie)
- Czy to prawda, że najstarsza z bilionów klasy jest milion razy większa niż najstarsza z miliona klas? (15 - tak, 16 - nie)
- Biorąc pod uwagę dwie liczby 637508 i 831. Czy to prawda, że najbardziej znacząca 1 z pierwszej liczby jest 1000 razy większa od najbardziej znaczącej 1 z drugiej liczby? (17 - tak, 18 - nie)
- Podano liczbę 432. Czy to prawda, że najbardziej znacząca jednostka bitowa tej liczby jest 2 razy większa niż najmłodsza? (19 - tak, 20 - nie)
- Biorąc pod uwagę liczbę 100 000 000. Czy to prawda, że liczba jednostek bitowych, które składają się na 10 000, wynosi 1000? (21 - tak, 22 - nie)
- Czy to prawda, że klasę bilionów poprzedza klasa biliardów, a klasę kwintylionów poprzedza ta klasa? (23 - tak, 24 - nie)
1.6. Z historii liczb
Od czasów starożytnych człowiek musiał liczyć liczbę rzeczy, porównywać liczbę przedmiotów (na przykład pięć jabłek, siedem strzał ...; w plemieniu jest 20 mężczyzn i trzydzieści kobiet, ... ). Istniała również potrzeba uporządkowania określonej liczby obiektów. Na przykład podczas polowania lider plemienia jest pierwszy, najsilniejszy wojownik plemienia jest drugi i tak dalej. Do tych celów wykorzystano liczby. Wymyślono dla nich specjalne imiona. W mowie nazywa się je cyframi: jeden, dwa, trzy itd. to liczby kardynalne, a pierwszy, drugi, trzeci to liczby porządkowe. Liczby zapisywano za pomocą znaków specjalnych - cyfr.
Z biegiem czasu pojawiły się systemy liczbowe. Są to systemy, które zawierają sposoby pisania liczb i różnych działań na nich. Najstarsze znane systemy liczbowe to egipski, babiloński i rzymski system liczbowy. W dawnej Rosji do pisania liczb używano liter alfabetu ze specjalnym znakiem ~ (titlo). System liczb dziesiętnych jest obecnie najczęściej używany. Powszechnie stosowane, zwłaszcza w świecie komputerowym, są systemy liczb binarnych, ósemkowych i szesnastkowych.
Tak więc, aby napisać ten sam numer, możesz użyć różnych znaków - liczb. Tak więc liczbę czterysta dwadzieścia pięć można zapisać cyframi egipskimi - hieroglify:
To jest egipski sposób pisania liczb. Ta sama liczba cyframi rzymskimi: CDXXV(Rzymski sposób zapisywania liczb) lub cyfr dziesiętnych 425 (zapis dziesiętny liczb). W notacji binarnej wygląda to tak: 110101001 (binarny lub binarny zapis liczb), a ósemkowo - 651 (notacja ósemkowa liczb). W notacji szesnastkowej zapiszemy: 1A9(zapis szesnastkowy). Możesz to zrobić po prostu: zrobić, jak Robinson Crusoe, czterysta dwadzieścia pięć nacięć (lub uderzeń) na drewnianym słupie - IIIIIIIII…... III. To są pierwsze obrazy liczb naturalnych.
Tak więc w dziesiętnym systemie zapisywania liczb (w dziesiętnym sposobie zapisywania liczb) używane są cyfry arabskie. Oto dziesięć różnych znaków - cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 . W systemie binarnym dwie cyfry binarne: 0, 1; ósemkowo - osiem cyfr ósemkowych: 0, 1, 2, 3, 4, 5, 6, 7; w systemie szesnastkowym - szesnaście różnych cyfr szesnastkowych: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F; w sześćdziesiętnym (babilońskim) - sześćdziesiąt różnych znaków - cyfry itp.)
Cyfry dziesiętne nadeszły do krajów europejskich z Bliskiego Wschodu, krajów arabskich. Stąd nazwa - cyfry arabskie. Ale przybyli do Arabów z Indii, gdzie wynaleziono je w połowie pierwszego tysiąclecia.
1.7. System cyfr rzymskich
Jednym ze starożytnych obecnie używanych systemów liczbowych jest system rzymski. W tabeli podajemy główne liczby systemu liczb rzymskich i odpowiadające im liczby systemu dziesiętnego.
|
cyfra rzymska |
C |
||||||
|
50 pięćdziesiąt |
500 pięćset |
1000 tysięcy |
System cyfr rzymskich to system dodawania. W nim, w przeciwieństwie do systemów pozycyjnych (na przykład dziesiętnych), każda cyfra oznacza tę samą liczbę. Tak, nagrywaj II- oznacza liczbę dwa (1 + 1 = 2), notacja III- cyfra trzy (1 + 1 + 1 = 3), notacja XXX- liczba trzydzieści (10 + 10 + 10 = 30) itd. Poniższe zasady dotyczą pisania liczb.
- Jeśli mniejsza liczba to po większy, to jest dodawany do większego: VII- numer siedem (5 + 2 = 5 + 1 + 1 = 7), XVII- numer siedemnaście (10 + 7 = 10 + 5 + 1 + 1 = 17), MCL- liczba tysiąc sto pięćdziesiąt (1000 + 100 + 50 = 1150).
- Jeśli mniejsza liczba to zanim większa, to jest odejmowana od większej: IX- numer dziewięć (9 = 10 - 1), LM- liczba dziewięćset pięćdziesiąt (1000-50 = 950).
Aby pisać duże liczby, musisz użyć (wymyślić) nowych znaków - liczb. Jednocześnie wpisy liczb okazują się kłopotliwe, bardzo trudno jest wykonywać obliczenia za pomocą cyfr rzymskich. Tak więc rok wystrzelenia pierwszego sztucznego satelity Ziemi (1957) w notacji rzymskiej ma postać MCMLVII .
Blok 1. 8. Karta dziurkacza
Czytanie liczb naturalnych
Zadania te są sprawdzane za pomocą mapy z okręgami. Wyjaśnijmy jego zastosowanie. Po wykonaniu wszystkich zadań i znalezieniu poprawnych odpowiedzi (są one oznaczone literami A, B, C itd.) umieść na karcie kartkę przezroczystego papieru. Zaznacz prawidłowe odpowiedzi znakami „X”, a także znakiem kombinacji „+”. Następnie połóż przezroczysty arkusz na stronie tak, aby pasowały do siebie znaczniki wyrównania. Jeśli wszystkie znaki „X” znajdują się w szarych kółkach na tej stronie, zadania zostały wykonane poprawnie.
1.9. Kolejność odczytu liczb naturalnych
Czytając liczbę naturalną, postępuj w następujący sposób.
- Umysłowo podziel liczbę na trójki (klasy) od prawej do lewej, od końca wpisu liczby.
- Zaczynając od klasy juniorów, od prawej do lewej (od końca wpisu liczbowego), spisują nazwy klas: jednostki, tysiące, miliony, miliardy, biliony, kwadrylionów, kwintyliony.
- Przeczytaj numer, zaczynając od szkoły średniej. W takim przypadku wywoływana jest liczba jednostek bitowych i nazwa klasy.
- Jeśli cyfrą jest zero (cyfra jest pusta), to nie jest wywoływana. Jeśli wszystkie trzy cyfry wywoływanej klasy są zerami (cyfry są puste), to ta klasa nie jest wywoływana.
Odczytajmy (nazwijmy) liczbę zapisaną w tabeli (patrz § 1), zgodnie z krokami 1 - 4. Podzielmy w myślach liczbę 38001102987000128425 na klasy od prawej do lewej: 038 001 102 987 000 128 425. Wskażmy nazwiska klasy w tej liczbie, począwszy od końca jej wpisy to: jednostki, tysiące, miliony, miliardy, biliony, kwadrylionów, kwintyliony. Teraz możesz przeczytać numer, zaczynając od klasy seniorów. Liczby trzycyfrowe, dwucyfrowe i jednocyfrowe nazywamy, dodając nazwę odpowiedniej klasy. Puste klasy nie są nazwane. Otrzymujemy następujący numer:
- 038 — trzydzieści osiem kwintylionów
- 001 - jeden biliard
- 102 - sto dwa biliony
- 987 - dziewięćset osiemdziesiąt siedem miliardów
- 000 - nie wymieniaj (nie czytaj)
- 128 - sto dwadzieścia osiem tysięcy
- 425 - czterysta dwadzieścia pięć
W efekcie liczbę naturalną 38 001 102 987 000 128 425 odczytujemy w następujący sposób: „trzydzieści osiem kwintylionów jeden kwadrylion sto dwa biliony dziewięćset osiemdziesiąt siedem miliardów sto dwadzieścia osiem tysięcy czterysta dwadzieścia pięć”.
1.9. Kolejność pisania liczb naturalnych
Liczby naturalne są zapisywane w następującej kolejności.
- Zapisz trzy cyfry dla każdej klasy, zaczynając od najwyższej klasy do cyfry jednostek. W takim przypadku dla starszej klasy liczb mogą być dwa lub jeden.
- Jeśli klasa lub ranga nie jest nazwana, w odpowiednich cyfrach zapisywane są zera.
Na przykład liczba dwadzieścia pięć milionów trzysta dwa zapisane w postaci: 25 000 302 (klasa tysiąca nie jest nazwana, dlatego zera są zapisywane we wszystkich cyfrach klasy tysiąca).
1.10. Reprezentacja liczb naturalnych jako suma wyrazów bitowych
Podajmy przykład: 7 563 429 to dziesiętna reprezentacja liczby siedem milionów pięćset sześćdziesiąt trzy tysiące czterysta dwadzieścia dziewięć. Ta liczba zawiera siedem milionów pięćset tysięcy sześć dziesiątek tysięcy trzy tysiące czterysta dwie dziesiątki i dziewięć jednostek. Można go przedstawić jako sumę: 7 563 429 \u003d 7 000 000 + 500 000 + 60 000 + + 3 000 + 400 + 20 + 9. Taki wpis nazywa się reprezentacją liczby naturalnej jako sumy terminów bitowych.
Blok 1.11. Zagrajmy
Skarby lochów
Na boisku znajduje się rysunek do bajki Kiplinga „Mowgli”. Pięć skrzyń ma kłódki. Aby je otworzyć, musisz rozwiązać problemy. W tym samym czasie, gdy otworzysz drewnianą skrzynię, otrzymasz jeden punkt. Gdy otworzysz blaszaną skrzynię, otrzymasz dwa punkty, miedzianą trzy punkty, srebrną cztery, a złotą pięć. Zwycięzcą jest ten, kto szybciej otworzy wszystkie skrzynie. W tę samą grę można grać na komputerze.
- drewniana skrzynia
Sprawdź, ile pieniędzy (w tysiącach rubli) znajduje się w tej skrzyni. Aby to zrobić, musisz znaleźć całkowitą liczbę najmniej znaczących jednostek bitowych klasy miliony dla liczby: 125308453231.
- Blaszana skrzynia
Sprawdź, ile pieniędzy (w tysiącach rubli) znajduje się w tej skrzyni. Aby to zrobić, w liczbie 12530845323 znajdź liczbę najmniej znaczących jednostek bitowych klasy jednostek i liczbę najmniej znaczących jednostek bitowych klasy milion. Następnie znajdź sumę tych liczb i po prawej stronie wpisz liczbę w dziesiątkach milionów.
- Miedziana skrzynia
Aby znaleźć pieniądze tej skrzyni (w tysiącach rubli), w liczbie 751305432198203 znajdź liczbę jednostek o najniższej cyfrze w klasie bilionów i liczbę jednostek o najniższej cyfrze w klasie miliardów. Następnie znajdź sumę tych liczb i po prawej stronie przypisz liczby naturalne klasy jednostek tej liczby w kolejności ich ułożenia.
- Srebrna skrzynia
Pieniądze tej skrzyni (w milionach rubli) zostaną pokazane przez sumę dwóch liczb: liczby jednostek o najniższej cyfrze klasy tysięcy i średniej liczby jednostek klasy miliard dla numeru 481534185491502.
- złota skrzynia
Biorąc pod uwagę numer 800123456789123456789. Jeśli pomnożymy liczby w najwyższych cyfrach wszystkich klas tej liczby, otrzymamy pieniądze tej skrzyni w milionach rubli.
Blok 1.12. Mecz
Napisz liczby naturalne. Reprezentacja liczb naturalnych jako suma wyrazów bitowych
Dla każdego zadania w lewej kolumnie wybierz rozwiązanie z prawej kolumny. Zapisz odpowiedź w formie: 1a; 2g; 3b…
|
Zapisz liczby: pięć milionów dwadzieścia pięć tysięcy |
|||
|
Zapisz liczby: pięć miliardów dwadzieścia pięć milionów |
|||
|
Zapisz liczby: pięć bilionów dwadzieścia pięć |
|||
|
Zapisz liczby: siedemdziesiąt siedem milionów siedemdziesiąt siedem tysięcy siedemset siedemdziesiąt siedem |
|||
|
Zapisz liczby: siedemdziesiąt siedem bilionów siedemset siedemdziesiąt siedem tysięcy siedem |
|||
|
Zapisz liczby: siedemdziesiąt siedem milionów siedemset siedemdziesiąt siedem tysięcy siedem |
|||
|
Zapisz liczby: sto dwadzieścia trzy miliardy czterysta pięćdziesiąt sześć milionów siedemset osiemdziesiąt dziewięć tysięcy |
|||
|
Zapisz liczby: sto dwadzieścia trzy miliony czterysta pięćdziesiąt sześć tysięcy siedemset osiemdziesiąt dziewięć |
|||
|
Zapisz liczby: trzy miliardy jedenaście |
|||
|
Zapisz liczby: trzy miliardy jedenaście milionów |
Opcja 2
|
trzydzieści dwa miliardy sto siedemdziesiąt pięć milionów dwieście dziewięćdziesiąt osiem tysięcy trzysta czterdzieści jeden |
100000000 + 1000000 + 10000 + 100 + 1 |
||
|
Wyraź liczbę jako sumę terminów bitowych: trzysta dwadzieścia jeden milionów czterdzieści jeden |
30000000000 + 2000000000 + 100000000 + 70000000 + 5000000 + 200000 + 90000 + 8000 + 300 + 40 + 1 |
||
|
Wyraź liczbę jako sumę terminów bitowych: 321000175298341 |
|||
|
Wyraź liczbę jako sumę terminów bitowych: 101010101 |
|||
|
Wyraź liczbę jako sumę terminów bitowych: 11111 |
300000000 + 20000000 + 1000000 + |
||
|
5000000 + 300000 + 20000 + 1000 |
|||
|
Zapisz w notacji dziesiętnej liczbę reprezentowaną jako suma terminów bitowych: 5000000 + 300 + 20 + 1 |
30000000000000 + 2000000000000 + 1000000000000 + 100000000 + 70000000 + 5000000 + 200000 + 90000 + 8000 + 300 + 40 + 1 |
||
|
Zapisz w notacji dziesiętnej liczbę reprezentowaną jako suma terminów bitowych: 10000000000 + 2000000000 + 100000 + 10 + 9 |
|||
|
Zapisz w notacji dziesiętnej liczbę reprezentowaną jako suma terminów bitowych: 10000000000 + 2000000000 + 100000000 + 10000000 + 9000000 |
|||
|
Zapisz w notacji dziesiętnej liczbę reprezentowaną jako suma terminów bitowych: 9000000000000 + 9000000000 + 9000000 + 9000 + 9 |
10000 + 1000 + 100 + 10 + 1 |
Blok 1.13. Test fasetowy
Nazwa testu pochodzi od słowa „złożone oko owadów”. Jest to oko złożone, składające się z oddzielnych „oczu”. Zadania testu fasetowego składają się z oddzielnych elementów, oznaczonych liczbami. Zazwyczaj testy aspektowe zawierają dużą liczbę elementów. Ale w tym teście są tylko cztery zadania, ale składają się one z dużej liczby elementów. Ma to na celu nauczenie Cię, jak „zbierać” problemy testowe. Jeśli potrafisz je skomponować, z łatwością poradzisz sobie z innymi testami aspektowymi.
Wyjaśnijmy, jak komponowane są zadania na przykładzie zadania trzeciego. Składa się z elementów testowych o numerach: 1, 4, 7, 11, 1, 5, 7, 9, 10, 16, 17, 22, 21, 25
« Jeśli» 1) weź liczby z tabeli (liczba); 4) 7; 7) umieść go w kategorii; 11) miliard; 1) weź numer ze stołu; 5) 8; 7) umieść go w szeregach; 9) dziesiątki milionów; 10) setki milionów; 16) setki tysięcy; 17) dziesiątki tysięcy; 22) umieść liczby 9 i 6 w tysiącach i setkach miejsc. 21) uzupełnij pozostałe cyfry zerami; " NASTĘPNIE» 26) otrzymujemy liczbę równą czasowi (okresowi) obrotu planety Pluton wokół Słońca w sekundach (s); " Ta liczba to»: 7880889600 s. W odpowiedziach jest to oznaczone literą "w".
Podczas rozwiązywania problemów napisz ołówkiem liczby w komórkach tabeli.
Test fasetowy. Wymyśl numer
Tabela zawiera liczby:
Jeśli
1) weź numer (liczby) z tabeli:
2) 4; 3) 5; 4) 7; 5) 8; 6) 9;
7) umieścić tę liczbę (cyfry) w kategorii (cyfry);
8) setki kwadrylionów i dziesiątki kwadrylionów;
9) dziesiątki milionów;
10) setki milionów;
11) miliard;
12) kwintyliony;
13) dziesiątki kwintylionów;
14) setki kwintylionów;
15) bilion;
16) setki tysięcy;
17) dziesiątki tysięcy;
18) wypełnić nią klasę (zajęcia);
19) kwintyliony;
20) mld;
21) w pozostałych cyfrach wpisać zera;
22) umieścić cyfry 9 i 6 w tysiącach i setkach miejsc;
23) otrzymujemy liczbę równą masie Ziemi w dziesiątkach ton;
24) otrzymujemy liczbę w przybliżeniu równą objętości Ziemi w metrach sześciennych;
25) otrzymujemy liczbę równą odległości (w metrach) od Słońca do najdalszej planety Układu Słonecznego Plutona;
26) otrzymujemy liczbę równą czasowi (okresowi) obrotu planety Pluton wokół Słońca w sekundach (s);
Ten numer to:
a) 5929000000000
b) 999990000000000000000
d) 5980000000000000000000
Rozwiązywać problemy:
1, 3, 6, 5, 18, 19, 21, 23
1, 6, 7, 14, 13, 12, 8, 21, 24
1, 4, 7, 11, 1, 5, 7, 10, 9, 16, 17, 22, 21, 26
1, 3, 7, 15, 1, 6, 2, 6, 18, 20, 21, 25
Odpowiedzi
1, 3, 6, 5, 18, 19, 21, 23 - g
1, 6, 7, 14, 13, 12, 8, 21, 24 - b
1, 4, 7, 11, 1, 5, 7, 10, 9, 16, 17, 22, 21, 26 - w
1, 3, 7, 15, 1, 6, 2, 6, 18, 20, 21, 25 - a
W matematyce istnieje kilka różnych zestawów liczb: rzeczywista, zespolona, całkowita, wymierna, niewymierna, ... W naszym Życie codzienne najczęściej posługujemy się liczbami naturalnymi, ponieważ spotykamy je podczas liczenia i wyszukiwania, wskazując liczbę obiektów.
W kontakcie z
Jakie liczby nazywają się naturalnymi?
Z dziesięciu cyfr możesz zapisać absolutnie dowolną istniejącą sumę klas i rang. Są to walory przyrodnicze które są używane:
- Licząc dowolne pozycje (pierwszy, drugi, trzeci, ... piąty, ... dziesiąty).
- Przy wskazywaniu ilości sztuk (jeden, dwa, trzy...)
Wartości N są zawsze liczbami całkowitymi i dodatnimi. Nie ma największego N, ponieważ zbiór wartości całkowitych nie jest ograniczony.
Uwaga! Liczby naturalne uzyskuje się przez liczenie przedmiotów lub wyznaczanie ich ilości.
Absolutnie dowolna liczba może być dekomponowana i reprezentowana jako terminy bitowe, na przykład: 8.346.809=8 milionów+346 tysięcy+809 jednostek.
Ustaw N
Zbiór N jest w zestawie rzeczywista, całkowita i dodatnia. Na diagramie zbioru byłyby one w sobie, ponieważ zbiór naturalnych jest ich częścią.
Zbiór liczb naturalnych jest oznaczony literą N. Zbiór ten ma początek, ale nie ma końca.
Istnieje również rozszerzony zestaw N, w którym zawiera się zero.
najmniejsza liczba naturalna
W większości szkół matematycznych najmniejsza wartość N liczone jako jednostka, ponieważ brak obiektów jest uważany za pusty.
Ale w zagranicznych szkołach matematycznych, na przykład po francusku, uważa się to za naturalne. Obecność zera w serii ułatwia dowód kilka twierdzeń.
Zbiór wartości N zawierający zero nazywany jest rozszerzonym i jest oznaczony symbolem N0 (indeks zerowy).
Szereg liczb naturalnych
N wiersz to sekwencja wszystkich N zestawów cyfr. Ta sekwencja nie ma końca.
Osobliwością serii naturalnej jest to, że następna liczba będzie się różnić o jeden od poprzedniej, to znaczy wzrośnie. Ale znaczenia nie może być ujemna.
Uwaga! Dla wygody liczenia istnieją klasy i kategorie:
- Jednostki (1, 2, 3),
- Dziesiątki (10, 20, 30),
- Setki (100, 200, 300),
- Tysiące (1000, 2000, 3000),
- Dziesiątki tysięcy (30 000),
- Setki tysięcy (800 000),
- Miliony (4000000) itp.
Wszystkie N
Wszystkie N są w zbiorze wartości rzeczywistych, całkowitych, nieujemnych. Oni są ich część integralna.
Wartości te idą w nieskończoność, mogą należeć do klas milionów, miliardów, kwintylionów itp.
Na przykład:
- Pięć jabłek, trzy kocięta,
- Dziesięć rubli, trzydzieści ołówków,
- Sto kilogramów, trzysta książek,
- Milion gwiazd, trzy miliony ludzi itd.
Sekwencja w N
W różnych szkołach matematycznych można znaleźć dwa przedziały, do których należy ciąg N:
od zera do plus nieskończoności włącznie z końcami i od jednego do plus nieskończoności włącznie z końcami, czyli wszystko pozytywne całe odpowiedzi.
N zestawów cyfr może być parzystych lub nieparzystych. Rozważ pojęcie dziwności.
Nieparzyste (wszelkie nieparzyste kończą się cyframi 1, 3, 5, 7, 9.) z dwoma mają resztę. Na przykład 7:2=3,5, 11:2=5,5, 23:2=11,5.
Co znaczy nawet N?
Wszelkie parzyste sumy klas kończą się liczbami: 0, 2, 4, 6, 8. Przy dzieleniu parzystego N przez 2 nie będzie reszty, czyli wynik jest całą odpowiedzią. Na przykład 50:2=25, 100:2=50, 3456:2=1728.
Ważny! Szereg liczbowy N nie może składać się tylko z wartości parzystych lub nieparzystych, ponieważ muszą się one zmieniać: po liczbie parzystej zawsze następuje liczba nieparzysta, potem znowu liczba parzysta i tak dalej.
N właściwości
Jak wszystkie inne zbiory, N ma swoje własne specjalne właściwości. Rozważ właściwości serii N (nierozszerzone).
- Wartość, która jest najmniejsza i nie następuje po żadnej innej, to jeden.
- N to ciąg, czyli jedna wartość naturalna podąża za innym(z wyjątkiem jednego - jest pierwszy).
- Kiedy wykonujemy operacje obliczeniowe na N sumach cyfr i klas (dodawanie, mnożenie), to w odpowiedzi zawsze wychodzi naturalnie oznaczający.
- W obliczeniach możesz używać permutacji i kombinacji.
- Każda kolejna wartość nie może być mniejsza od poprzedniej. Również w serii N będzie działać następujące prawo: jeśli liczba A jest mniejsza niż B, to w serii liczb zawsze będzie C, dla którego równość jest prawdziwa: A + C \u003d B.
- Jeśli weźmiemy dwa naturalne wyrażenia, na przykład A i B, wówczas jedno z wyrażeń będzie dla nich prawdziwe: A \u003d B, A jest większe niż B, A jest mniejsze niż B.
- Jeśli A jest mniejsze niż B, a B jest mniejsze niż C, to wynika z tego, że że A jest mniejsze niż C.
- Jeśli A jest mniejsze niż B, to wynika z tego, że: jeśli dodamy do nich to samo wyrażenie (C), to A + C jest mniejsze niż B + C. Prawdą jest też, że jeśli te wartości pomnożymy przez C, to AC jest mniejsze niż AB.
- Jeśli B jest większe niż A, ale mniejsze niż C, to B-A jest mniejsze niż C-A.
Uwaga! Wszystkie powyższe nierówności obowiązują również w odwrotnym kierunku.
Jak nazywa się składowe mnożenia?
W wielu prostych, a nawet złożonych zadaniach znalezienie odpowiedzi zależy od umiejętności uczniów.
Aby szybko i poprawnie mnożyć i móc rozwiązywać problemy odwrotne, musisz znać elementy mnożenia.
15. 10=150. W tym wyrażeniu 15 i 10 są czynniki, a 150 to produkt.
Mnożenie ma właściwości, które są niezbędne przy rozwiązywaniu problemów, równań i nierówności:
- Zmiana układu czynników nie zmienia produktu końcowego.
- Aby znaleźć nieznany czynnik, musisz podzielić iloczyn przez znany czynnik (ważny dla wszystkich czynników).
Na przykład: 15 . X=150. Podziel produkt według znanego czynnika. 150:15=10. Sprawdźmy. piętnaście . 10=150. Zgodnie z tą zasadą nawet złożone równania liniowe(jeśli je uprościsz).
Ważny! Produkt może składać się z więcej niż dwóch czynników. Na przykład: 840=2 . 5. 7. 3. 4
Czym są liczby naturalne w matematyce?
Wyładowania i klasy liczb naturalnych
Wniosek
Podsumujmy. N jest używane podczas liczenia lub wskazywania liczby sztuk. Liczba naturalnych zbiorów cyfr jest nieskończona, ale zawiera tylko liczby całkowite i dodatnie sumy cyfr i klas. Mnożenie jest również konieczne dla liczyć rzeczy, a także do rozwiązywania problemów, równań i różnych nierówności.
Matematyka wyłoniła się z filozofii ogólnej około VI wieku p.n.e. e. i od tego momentu rozpoczęła się jej zwycięski marsz dookoła świata. Każdy etap rozwoju wnosił coś nowego - ewoluowało liczenie elementarne, przekształcało się w rachunek różniczkowy i całkowy, zmieniały się wieki, formuły stawały się coraz bardziej zagmatwane, a nadszedł moment, kiedy "zaczęła się najbardziej skomplikowana matematyka - zniknęły z niej wszystkie liczby". Ale jaka była podstawa?
Początek czasu
Liczby naturalne pojawiły się wraz z pierwszymi działaniami matematycznymi. Kiedyś kolce, dwa kolce, trzy kolce... Pojawiły się dzięki indyjskim naukowcom, którzy wydedukowali pierwszy pozycyjny
Słowo „pozycjonowanie” oznacza, że położenie każdej cyfry w liczbie jest ściśle określone i odpowiada jej kategorii. Na przykład liczby 784 i 487 są tymi samymi liczbami, ale liczby nie są równoważne, ponieważ pierwsza obejmuje 7 setek, a druga tylko 4. Innowację Indian podchwycili Arabowie, którzy przynieśli liczby do forma, którą znamy teraz.
W czasach starożytnych liczbom nadawano mistyczne znaczenie, Pitagoras wierzył, że liczba stanowi podstawę stworzenia świata wraz z głównymi elementami - ogniem, wodą, ziemią, powietrzem. Jeśli rozważamy wszystko tylko od strony matematycznej, to czym jest liczba naturalna? Ciało liczb naturalnych jest oznaczone jako N i jest nieskończonym ciągiem liczb całkowitych i dodatnich: 1, 2, 3, … + ∞. Zero jest wykluczone. Służy głównie do liczenia sztuk i wskazywania kolejności.
Co jest w matematyce? Aksjomaty Peano
Pole N jest ciałem bazowym, na którym opiera się matematyka elementarna. Z biegiem czasu pola liczb całkowitych, wymierne,
Praca włoskiego matematyka Giuseppe Peano umożliwiła dalszą strukturyzację arytmetyki, osiągnęła jej formalność i utorowała drogę do dalszych wniosków wykraczających poza dziedzinę N.
Co to jest liczba naturalna zostało wyjaśnione wcześniej prostym językiem, poniżej rozważymy definicję matematyczną opartą na aksjomatach Peano.
- Jedna jest uważana za liczbę naturalną.
- Liczba następująca po liczbie naturalnej jest liczbą naturalną.
- Nie ma liczby naturalnej przed jedynką.
- Jeśli liczba b występuje zarówno po liczbie c, jak i po liczbie d, to c=d.
- Aksjomat indukcji, który z kolei pokazuje, czym jest liczba naturalna: jeśli jakieś twierdzenie zależne od parametru jest prawdziwe dla liczby 1, to zakładamy, że działa również dla liczby n z ciała liczb naturalnych N. Wtedy twierdzenie to jest również prawdziwe dla n =1 z ciała liczb naturalnych N.
Podstawowe operacje na ciele liczb naturalnych
Ponieważ pole N stało się pierwszym dla obliczeń matematycznych, odnoszą się do niego zarówno dziedziny definicji, jak i zakresy wartości szeregu operacji. Są zamknięte i nie. Główna różnica polega na tym, że zamknięte operacje gwarantują pozostawienie wyniku w zbiorze N, bez względu na to, jakie liczby są zaangażowane. Wystarczy, że są naturalne. Wynik pozostałych interakcji liczbowych nie jest już tak jednoznaczny i zależy bezpośrednio od tego, jakie liczby są zawarte w wyrażeniu, ponieważ może to być sprzeczne z główną definicją. Czyli operacje zamknięte:
- dodanie - x + y = z, gdzie x, y, z są zawarte w polu N;
- mnożenie - x * y = z, gdzie x, y, z są zawarte w polu N;
- potęgowanie - x y , gdzie x, y są zawarte w polu N.
Pozostałe operacje, których wynik może nie istnieć w kontekście definicji „co to jest liczba naturalna”, to:
Własności liczb należących do pola N
Całe dalsze rozumowanie matematyczne będzie oparte na następujących właściwościach, najbardziej trywialnych, ale nie mniej ważnych.
- Przemienność dodawania to x + y = y + x, gdzie liczby x, y są zawarte w polu N. Lub dobrze znane „suma nie zmienia się od zmiany miejsc wyrazów”.
- Przemienność mnożenia to x * y = y * x, gdzie liczby x, y są zawarte w polu N.
- Asocjacyjna własność dodawania to (x + y) + z = x + (y + z), gdzie x, y, z są zawarte w polu N.
- Asocjacyjna własność mnożenia to (x * y) * z = x * (y * z), gdzie liczby x, y, z są zawarte w polu N.
- własność rozkładu - x (y + z) = x * y + x * z, gdzie liczby x, y, z są zawarte w polu N.
Tabela pitagorejska
Jednym z pierwszych kroków w poznawaniu całej struktury matematyki elementarnej przez uczniów, po tym, jak sami zrozumieli, jakie liczby nazywamy naturalnymi, jest tablica pitagorejska. Można go rozpatrywać nie tylko z punktu widzenia nauki, ale także jako cenny zabytek naukowy.
Ta tabliczka mnożenia przeszła wiele zmian w czasie: usunięto z niej zero, a liczby od 1 do 10 oznaczają same siebie, bez uwzględniania kolejności (setki, tysiące…). Jest to tabela, w której nagłówki wierszy i kolumn są liczbami, a zawartość komórek ich przecięcia jest równa ich iloczynowi.
W praktyce nauczania w ostatnich dziesięcioleciach pojawiła się potrzeba zapamiętywania tablicy pitagorejskiej „w porządku”, to znaczy zapamiętywanie było pierwsze. Mnożenie przez 1 zostało wykluczone, ponieważ wynik wynosił 1 lub więcej. Tymczasem w tabeli gołym okiem widać wzór: iloczyn liczb rośnie o jeden krok, który jest równy tytułowi wiersza. Zatem drugi czynnik pokazuje nam, ile razy musimy brać pierwszy, aby uzyskać pożądany produkt. Ten system jest znacznie wygodniejszy niż ten praktykowany w średniowieczu: nawet rozumiejąc, czym jest liczba naturalna i jak bardzo jest trywialna, ludziom udało się skomplikować swoje codzienne liczenie za pomocą systemu opartego na potęgach dwójki.
Podzbiór jako kolebka matematyki
W chwili obecnej ciało liczb naturalnych N jest traktowane tylko jako jeden z podzbiorów liczb zespolonych, co nie czyni ich mniej wartościowymi w nauce. Liczba naturalna to pierwsza rzecz, której dziecko uczy się, studiując siebie i otaczający go świat. Jeden palec, dwa palce… Dzięki niemu człowiek rozwija logiczne myślenie, a także umiejętność ustalania przyczyny i wywnioskowania skutku, torując drogę do wielkich odkryć.
Liczby naturalne to jedno z najstarszych pojęć matematycznych.
W odległej przeszłości ludzie nie znali liczb, a kiedy trzeba było policzyć przedmioty (zwierzęta, ryby itp.), robili to inaczej niż my teraz.
Liczbę przedmiotów porównano z częściami ciała, na przykład z palcami dłoni, i powiedzieli: „Mam tyle orzechów, ile jest palców na dłoni”.
Z biegiem czasu ludzie zdali sobie sprawę, że pięć orzechów, pięć kóz i pięć zajęcy ma wspólną własność – ich liczba to pięć.
Pamiętać!
Liczby całkowite to liczby, zaczynające się od 1, uzyskane podczas liczenia obiektów.
1, 2, 3, 4, 5…
najmniejsza liczba naturalna — 1 .
największa liczba naturalna nie istnieje.
Podczas liczenia liczba zero nie jest używana. Dlatego zero nie jest uważane za liczbę naturalną.
Ludzie nauczyli się pisać liczby znacznie później niż liczyć. Przede wszystkim zaczęli przedstawiać jednostkę jednym kijem, potem dwoma kijami – cyfrą 2, trzema – cyfrą 3.
| — 1, || — 2, ||| — 3, ||||| — 5 …
Potem pojawiły się specjalne znaki do oznaczania liczb - prekursorów współczesnych liczb. Liczby, których używamy do zapisywania liczb, pochodzą z Indii około 1500 lat temu. Arabowie przywieźli je do Europy, dlatego nazywają się cyfry arabskie.
W sumie jest dziesięć cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Cyfry te mogą służyć do zapisania dowolnej liczby naturalnej.
Pamiętać!
seria naturalna jest ciągiem wszystkich liczb naturalnych:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …
W szeregu naturalnym każda liczba jest większa od poprzedniej o 1.
Szereg naturalny jest nieskończony, nie ma w nim największej liczby naturalnej.
System liczenia, którego używamy, nazywa się pozycyjny dziesiętny.
Dziesiętny, ponieważ 10 jednostek każdej cyfry tworzy 1 jednostkę najbardziej znaczącej cyfry. Pozycyjna, ponieważ wartość cyfry zależy od jej miejsca w zapisie liczby, czyli od cyfry, w której jest zapisana.
Ważny!
Klasy następujące po miliardzie są nazwane zgodnie z łacińskimi nazwami liczb. Każda następna jednostka zawiera tysiąc poprzednich.
- 1000 miliardów = 1 000 000 000 000 = 1 bilion („trzy” to po łacinie „trzy”)
- 1000 bilionów = 1 000 000 000 000 000 = 1 biliard ("quadra" to po łacinie "cztery")
- 1000 biliardów = 1 000 000 000 000 000 000 = 1 kwintillion ("quinta" to po łacinie "pięć")
Jednak fizycy odkryli liczbę, która przewyższa liczbę wszystkich atomów (najmniejszych cząstek materii) w całym wszechświecie.
Ten numer ma specjalną nazwę - googol. Googol to liczba, która ma 100 zer.
