Valore naturale. Numeri naturali - Nozioni di base

I numeri sono un concetto astratto. Sono una caratteristica quantitativa degli oggetti e possono essere reali, razionali, negativi, interi e frazionari, oltre che naturali.

La serie naturale viene solitamente utilizzata durante il conteggio, in cui compaiono naturalmente le notazioni di quantità. La conoscenza del conteggio inizia nella prima infanzia. Quale bambino ha evitato rime divertenti che utilizzavano elementi di conteggio naturale? "Uno, due, tre, quattro, cinque... Il coniglietto è uscito a fare una passeggiata!" oppure "1, 2, 3, 4, 5, 6, 7, 8, 9, 10, il re ha deciso di impiccarmi..."

Per ogni numero naturale ne puoi trovare un altro maggiore. Questo insieme è solitamente indicato con la lettera N e deve essere considerato infinito nella direzione dell'aumento. Ma questo set ha un inizio: è uno di essi. Sebbene ci siano numeri naturali francesi, il cui insieme include anche lo zero. Ma la principale caratteristica distintiva di entrambi gli insiemi è il fatto che non includono né numeri frazionari né numeri negativi.

La necessità di contare una varietà di oggetti è nata in epoca preistorica. Quindi si suppone che si sia formato il concetto di "numeri naturali". La sua formazione è avvenuta durante l’intero processo di cambiamento della visione del mondo di una persona e dello sviluppo della scienza e della tecnologia.

Tuttavia, non potevano ancora pensare in modo astratto. Era difficile per loro capire quale fosse la comunanza dei concetti di “tre cacciatori” o “tre alberi”. Pertanto, quando si indica il numero di persone, è stata utilizzata una definizione e quando si indica lo stesso numero di oggetti di tipo diverso, è stata utilizzata una definizione completamente diversa.

Ed è stato estremamente breve. Conteneva solo i numeri 1 e 2 e il conteggio terminava con i concetti di “molti”, “branco”, “folla”, “mucchio”.

Successivamente è stato formato un resoconto più progressivo e più ampio. Un fatto interessante è che c'erano solo due numeri: 1 e 2, e i numeri successivi sono stati ottenuti sommando.

Un esempio di ciò sono le informazioni che ci sono pervenute sulle serie numeriche della tribù australiana, che avevano 1 per la parola “Enza” e 2 per la parola “petcheval”. Il numero 3 suonava quindi “petcheval-Enza”, e il 4 suonava “petcheval-petcheval”.

La maggior parte delle persone riconosceva le dita come lo standard per contare. L'ulteriore sviluppo del concetto astratto di "numeri naturali" ha seguito il percorso dell'utilizzo delle tacche su un bastoncino. E allora è stato necessario designarne una dozzina con un altro segno. Gli antichi trovarono la nostra via d'uscita: iniziarono a usare un altro bastone, sul quale furono fatte delle tacche per indicare le decine.

La capacità di riprodurre i numeri si espanse enormemente con l'avvento della scrittura. Inizialmente i numeri venivano raffigurati come linee su tavolette di argilla o papiro, ma gradualmente iniziarono ad essere utilizzate altre icone di scrittura: è così che apparvero i numeri romani.

Molto più tardi apparvero quelli che aprirono la possibilità di scrivere numeri con un insieme di caratteri relativamente piccolo. Oggi non è difficile scrivere numeri così grandi come la distanza tra i pianeti e il numero di stelle. Devi solo imparare a usare i gradi.

Euclide nel 3 ° secolo aC nel libro "Elementi" stabilisce l'infinito dell'insieme numerico e Archimede in "Psamita" rivela i principi per costruire i nomi di numeri arbitrariamente grandi. Quasi fino alla metà del XIX secolo non si trovò di fronte alla necessità di una formulazione chiara del concetto di “numeri naturali”. La definizione si è resa necessaria con l'avvento del metodo matematico assiomatico.

E negli anni '70 del XIX secolo formulò una chiara definizione di numeri naturali, basata sul concetto di insieme. E oggi sappiamo già che i numeri naturali sono tutti interi, da 1 a infinito. I bambini piccoli, facendo il primo passo per conoscere la regina di tutte le scienze, la matematica, iniziano a studiare proprio questi numeri.

1.1.Definizione

I numeri che le persone usano quando contano vengono chiamati naturale(ad esempio uno, due, tre,..., cento, centouno,..., tremiladuecentoventuno,...) Per scrivere i numeri naturali si utilizzano segni (simboli) speciali, chiamato in numeri.

Al giorno d'oggi è accettato sistema di numeri decimali. Il sistema decimale (o metodo) di scrittura dei numeri utilizza numeri arabi. Questi sono dieci diversi caratteri numerici: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 .

Meno un numero naturale è un numero uno, esso scritto utilizzando un numero decimale - 1. Il numero naturale successivo si ottiene dal precedente (tranne uno) aggiungendo 1 (uno). Questa somma può essere fatta più volte (un numero infinito di volte). Significa che NO il più grande numero naturale. Pertanto dicono che la serie dei numeri naturali è illimitata o infinita, poiché non ha fine. I numeri naturali vengono scritti utilizzando cifre decimali.

1.2. Numero "zero"

Per indicare l'assenza di qualcosa utilizzare il numero " zero" O " zero". È scritto usando i numeri 0 (zero). Ad esempio, in una scatola tutte le palline sono rosse. Quanti di loro sono verdi? - Risposta: zero . Ciò significa che non ci sono palline verdi nella scatola! Il numero 0 può significare che qualcosa è finito. Ad esempio, Masha aveva 3 mele. Ne ha condivisi due con gli amici e ne ha mangiato uno lei stessa. Quindi se n'è andata 0 (zero) mele, ad es. non ne è rimasto nemmeno uno. Il numero 0 potrebbe significare che qualcosa non è successo. Ad esempio, la partita di hockey Team Russia - Team Canada si è conclusa con un punteggio 3:0 (leggi “tre - zero”) a favore della squadra russa. Ciò significa che la squadra russa ha segnato 3 gol, mentre la squadra canadese ha segnato 0 gol e non è riuscita a segnarne nemmeno uno. Dobbiamo ricordare che il numero zero non è un numero naturale.

1.3. Scrivere i numeri naturali

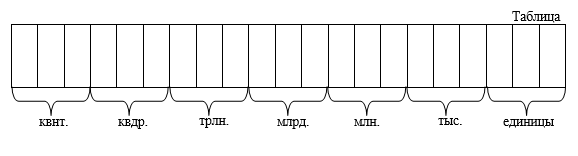
Nel modo decimale di scrivere un numero naturale, ogni cifra può rappresentare un numero diverso. Dipende dalla posizione di questa cifra nel record del numero. Viene chiamato un certo posto nella notazione di un numero naturale posizione. Pertanto, viene chiamato il sistema numerico decimale posizionale. Considera la notazione decimale di 7777 settemilasettecentosettantasette. Questa voce contiene settemilasettecentosette decine e sette unità.

Viene chiamata ciascuna delle posizioni (posizioni) nella notazione decimale di un numero scarico. Ogni tre cifre vengono combinate in Classe. Questa fusione viene eseguita da destra a sinistra (dalla fine del record numerico). Varie categorie e classi hanno i propri nomi. La gamma dei numeri naturali è illimitata. Pertanto, anche il numero di gradi e classi non è limitato ( infinitamente). Diamo un'occhiata ai nomi delle cifre e delle classi usando l'esempio di un numero con notazione decimale

38 001 102 987 000 128 425:

Classi e gradi
quintilioni		centinaia di quintilioni
		decine di quintilioni
		quintilioni
quadrilioni		centinaia di quadrilioni
		decine di quadrilioni
		quadrilioni
trilioni		centinaia di trilioni
		decine di trilioni
		trilioni
miliardi		centinaia di miliardi
		decine di miliardi
		miliardi
milioni		centinaia di milioni
		decine di milioni
		milioni
		centinaia di migliaia
		decine di migliaia

Quindi, le classi, a cominciare dalle più giovani, hanno nomi: unità, migliaia, milioni, miliardi, trilioni, quadrilioni, quintilioni.

1.4. Unità di bit

Ciascuna delle classi nella notazione dei numeri naturali è composta da tre cifre. Ogni grado ha unità di cifre. I seguenti numeri sono chiamati unità di cifra:

1 cifra unità di unità cifra,

Unità di 10 cifre delle decine,

100 - unità di centinaia di cifre,

1 000 - unità di migliaia di cifre,

10.000 è un'unità di luogo di decine di migliaia,

100.000 è un'unità di luogo per centinaia di migliaia,

1.000.000 è l'unità di milioni di cifre, ecc.

Un numero in una qualsiasi delle cifre mostra il numero di unità di questa cifra. Pertanto, il numero 9, nella posizione delle centinaia di miliardi, significa che il numero 38.001.102.987.000 128.425 include nove miliardi (cioè 9 volte 1.000.000.000 o unità a 9 cifre della posizione dei miliardi). Un posto vuoto per centinaia di quintilioni significa che non ci sono centinaia di quintilioni nel numero indicato o che il loro numero è zero. In questo caso il numero 38 001 102 987 000 128 425 può essere scritto così: 038 001 102 987 000 128 425.

Puoi scriverlo diversamente: 000 038 001 102 987 000 128 425. Gli zeri all'inizio del numero indicano cifre vuote di ordine superiore. Di solito non vengono scritti, a differenza degli zeri all'interno della notazione decimale, che necessariamente contrassegnano le cifre vuote. Pertanto, tre zeri nella classe dei milioni significano che le centinaia di milioni, le decine di milioni e le unità di milioni sono vuote.

1.5. Abbreviazioni per scrivere i numeri

Quando si scrivono i numeri naturali si usano le abbreviazioni. Ecco alcuni esempi:

1.000 = 1 mille (mille)

23.000.000 = 23 milioni (ventitre milioni)

5.000.000.000 = 5 miliardi (cinque miliardi)

203.000.000.000.000 = 203 trilioni. (duecentotre trilioni)

107.000.000.000.000.000 = 107 metri quadrati. (centosette quadrilioni)

1.000.000.000.000.000.000 = 1 kwt. (un quintilione)

Blocco 1.1. Dizionario

Compilare un dizionario di nuovi termini e definizioni dal §1. Per fare ciò, scrivi le parole dall'elenco di termini sottostante nelle celle vuote. Nella tabella (alla fine del blocco), indicare per ciascuna definizione il numero del termine dell'elenco.

Blocco 1.2. Autopreparazione

Nel mondo dei grandi numeri

Economia .

1. Il budget della Russia per il prossimo anno sarà: 6328251684128 rubli.
2. Le spese previste per quest'anno sono: 5124983252134 rubli.
3. Le entrate del paese hanno superato le spese di 1203268431094 rubli.

Domande e compiti

1. Leggi tutti e tre i numeri indicati
2. Scrivi le cifre nella classe dei milioni per ciascuno dei tre numeri.

1. A quale sezione di ciascun numero appartiene la cifra che si trova nella settima posizione dalla fine del record numerico?
2. Quale numero di unità di cifra è indicato dal numero 2 nell'inserimento del primo numero?... nell'inserimento del secondo e del terzo numero?
3. Assegna un nome all'unità di cifra per l'ottava posizione dalla fine nella notazione di tre numeri.

Geografia (lunghezza)

1. Raggio equatoriale della Terra: 6378245 m
2. Circonferenza dell'equatore: 40075696 m
3. La massima profondità degli oceani del mondo (Fossa delle Marianne nell'Oceano Pacifico) 11500 m

Domande e compiti

1. Converti tutti e tre i valori in centimetri e leggi i numeri risultanti.
2. Per il primo numero (in cm), annota i numeri nelle sezioni:

centinaia di migliaia _______

decine di milioni _______

migliaia _______

miliardi _______

centinaia di milioni _______

1. Per il secondo numero (in cm), annota le unità di cifra corrispondenti ai numeri 4, 7, 5, 9 nella notazione numerica

1. Converti il ​​terzo valore in millimetri e leggi il numero risultante.
2. Per tutte le posizioni nell'inserimento della terza cifra (in mm), indicare le cifre e le unità delle cifre nella tabella:

Geografia (piazza)

1. L'area dell'intera superficie della Terra è di 510.083 mila chilometri quadrati.
2. La superficie delle somme sulla Terra è di 148.628 mila chilometri quadrati.
3. L'area della superficie dell'acqua terrestre è di 361.455 mila chilometri quadrati.

Domande e compiti

1. Converti tutti e tre i valori in metri quadrati e leggi i numeri risultanti.
2. Assegna un nome alle classi e alle categorie corrispondenti alle cifre diverse da zero nella registrazione di questi numeri (in mq).
3. Nello scrivere il terzo numero (in mq), nominare le unità di cifre corrispondenti ai numeri 1, 3, 4, 6.
4. In due voci del secondo valore (in kmq. e mq), indicare a quali cifre appartiene il numero 2.
5. Scrivi le unità del valore posizionale per la cifra 2 nelle seconde notazioni di quantità.

Blocco 1.3. Dialogo con il computer.

È noto che in astronomia vengono spesso utilizzati grandi numeri. Facciamo degli esempi. La distanza media della Luna dalla Terra è di 384mila km. La distanza della Terra dal Sole (media) è di 149.504 mila km, la Terra da Marte è di 55 milioni di km. Su un computer, utilizzando l'editor di testo Word, creare tabelle in modo che ciascuna cifra nella voce dei numeri indicati si trovi in ​​una cella (cella) separata. Per fare ciò, esegui i comandi sulla barra degli strumenti: tabella → aggiungi tabella → numero di righe (usa il cursore per impostare “1”) → numero di colonne (calcola tu stesso). Crea tabelle per altri numeri (nel blocco “Autopreparazione”).

Blocco 1.4. Relè dei grandi numeri

La prima riga della tabella contiene un numero elevato. Leggilo. Quindi completa le attività: spostando i numeri nel record del numero a destra o a sinistra, prendi i numeri successivi e leggili. (Non spostare gli zeri alla fine del numero!). In classe il testimone può essere portato avanti passandoselo a vicenda.

Linea 2 . Sposta tutte le cifre del numero nella prima riga verso sinistra attraverso due celle. Sostituisci i numeri 5 con il numero successivo. Riempi le celle vuote con zeri. Leggi il numero.

Linea 3 . Sposta tutte le cifre del numero nella seconda riga a destra attraverso tre celle. Sostituisci i numeri 3 e 4 nel numero con i seguenti numeri. Riempi le celle vuote con zeri. Leggi il numero.

Linea 4. Sposta tutte le cifre del numero nella riga 3 di una cella a sinistra. Sostituisci il numero 6 nella classe dei trilioni con il precedente e nella classe dei miliardi con il numero successivo. Riempi le celle vuote con zeri. Leggi il numero risultante.

Linea 5 . Sposta tutte le cifre del numero nella riga 4 di una cella a destra. Sostituisci il numero 7 nella categoria “decine di migliaia” con il precedente e nella categoria “decine di milioni” con quello successivo. Leggi il numero risultante.

Linea 6 . Sposta tutte le cifre del numero nella riga 5 a sinistra attraverso 3 celle. Sostituisci il numero 8 nella posizione delle centinaia di miliardi con il precedente, e il numero 6 nella posizione delle centinaia di milioni con il numero successivo. Riempi le celle vuote con zeri. Calcola il numero risultante.

Linea 7 . Sposta tutte le cifre del numero nella riga 6 nella cella a destra. Scambia i numeri nelle decine di quadrilioni e nelle decine di miliardi di posti. Leggi il numero risultante.

Linea 8 . Sposta tutte le cifre del numero nella riga 7 a sinistra attraverso una cella. Scambia i numeri nei quintilioni e nei quadrilioni di posti. Riempi le celle vuote con zeri. Leggi il numero risultante.

Linea 9 . Sposta tutte le cifre del numero nella riga 8 verso destra attraverso tre celle. Scambia due cifre adiacenti delle classi dei milioni e dei trilioni in una linea numerica. Leggi il numero risultante.

Linea 10 . Sposta tutte le cifre del numero nella riga 9 di una cella a destra. Leggi il numero risultante. Seleziona i numeri che indicano l'anno delle Olimpiadi di Mosca.

Blocco 1.5. giochiamo

Accendi la fiamma

Il campo da gioco è il disegno di un albero di Natale. Ha 24 lampadine. Ma solo 12 di essi sono collegati alla rete elettrica. Per selezionare le lampade collegate è necessario rispondere correttamente alle domande con “Sì” o “No”. Lo stesso gioco può essere fatto su un computer; la risposta corretta “accende” la lampadina.

1. È vero che i numeri sono segni speciali per scrivere i numeri naturali? (1 - sì, 2 - no)
2. È vero che 0 è il numero naturale più piccolo? (3 - sì, 4 - no)
3. È vero che nel sistema numerico posizionale la stessa cifra può rappresentare numeri diversi? (5 - sì, 6 - no)
4. È vero che una certa posizione nella notazione decimale dei numeri si chiama luogo? (7 - sì, 8 - no)
5. Viene fornito il numero 543.384. È vero che il numero delle unità con la cifra più alta è 543 e le cifre più basse sono 384? (9 - sì, 10 - no)
6. È vero che nella classe dei miliardi, la cifra più alta è cento miliardi e quella più bassa è un miliardo? (11 - sì, 12 - no)
7. Viene fornito il numero 458.121. È vero che la somma del numero delle unità con la cifra più alta e del numero di quelle con la cifra più bassa è 5? (13 - sì, 14 - no)
8. È vero che l’unità con la cifra più alta nella classe dei trilioni è un milione di volte più grande dell’unità con la cifra più alta nella classe dei milioni? (15 - sì, 16 - no)
9. Dati due numeri 637.508 e 831. È vero che l'unità di cifra più alta del primo numero è 1000 volte maggiore dell'unità di cifra più alta del secondo numero? (17 - sì, 18 - no)
10. Dato il numero 432. È vero che l'unità della cifra più alta di questo numero è 2 volte più grande della più bassa? (19 - sì, 20 - no)
11. Viene fornito il numero 100.000.000. È vero che il numero di unità di cifre che compongono 10.000 è uguale a 1000? (21 - sì, 22 - no)
12. È vero che prima della classe dei trilioni c’è la classe dei quadrilioni, e prima di questa classe c’è la classe dei quintilioni? (23 - sì, 24 - no)

1.6. Dalla storia dei numeri

Fin dall'antichità gli uomini si sono trovati di fronte alla necessità di contare il numero delle cose, confrontare le quantità di oggetti (ad esempio, cinque mele, sette frecce...; in una tribù ci sono 20 uomini e trenta donne,... ). C'era anche la necessità di stabilire un ordine all'interno di un certo numero di oggetti. Ad esempio, durante la caccia, il capo della tribù inizia per primo, il guerriero più forte della tribù arriva per secondo, ecc. Per questi scopi venivano utilizzati i numeri. Per loro furono inventati nomi speciali. Nel parlato si chiamano numeri: uno, due, tre, ecc. sono numeri cardinali, e il primo, secondo, terzo sono numeri ordinali. I numeri sono stati scritti utilizzando caratteri speciali: i numeri.

Nel corso del tempo è apparso sistemi numerici. Si tratta di sistemi che includono modi per scrivere numeri ed eseguire varie operazioni su di essi. I più antichi sistemi numerici conosciuti sono il sistema numerico egiziano, babilonese e romano. Nell'antichità, nella Rus', per scrivere i numeri venivano usate le lettere dell'alfabeto con un segno speciale ~ (titolo). Attualmente, il sistema di numerazione decimale è quello più utilizzato. I sistemi numerici binari, ottali ed esadecimali sono ampiamente utilizzati, soprattutto nel mondo dei computer.

Quindi, per scrivere lo stesso numero, puoi usare segni diversi: numeri. Quindi, il numero quattrocentoventicinque può essere scritto in numeri egiziani - geroglifici:

Questo è il modo egiziano di scrivere i numeri. Questo è lo stesso numero in numeri romani: CDXXV(modo romano di scrivere i numeri) o cifre decimali 425 (sistema di numerazione decimale). Nella notazione binaria appare così: 110101001 (sistema di numerazione binario o binario) e in ottale - 651 (sistema di numerazione ottale). Nel sistema numerico esadecimale verrà scritto: 1A9(sistema numerico esadecimale). Puoi farlo in modo molto semplice: fai, come Robinson Crusoe, quattrocentoventicinque tacche (o tratti) su un palo di legno - IIIIIIIII…... III. Queste sono le primissime immagini dei numeri naturali.

Quindi, nel sistema decimale di scrittura dei numeri (nel modo decimale di scrittura dei numeri) vengono utilizzati i numeri arabi. Questi sono dieci simboli diversi - numeri: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 . In binario: due cifre binarie: 0, 1; in ottale - otto cifre ottali: 0, 1, 2, 3, 4, 5, 6, 7; in esadecimale - sedici diverse cifre esadecimali: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F; in sessagesimale (babilonese) - sessanta caratteri diversi - numeri, ecc.)

I numeri decimali sono arrivati ​​​​ai paesi europei dal Medio Oriente e dai paesi arabi. Da qui il nome - Numeri arabi. Ma arrivarono agli arabi dall'India, dove furono inventati intorno alla metà del primo millennio.

1.7. Sistema numerico romano

Uno degli antichi sistemi numerici utilizzati oggi è il sistema romano. Presentiamo nella tabella i numeri principali del sistema numerico romano e i numeri corrispondenti del sistema decimale.

numero romano					C
				50 cinquanta		500 cinquecento	1000mila

Il sistema numerico romano è sistema di addizione. In esso, a differenza dei sistemi posizionali (ad esempio decimali), ogni cifra rappresenta lo stesso numero. Sì, registra II- denota il numero due (1 + 1 = 2), notazione III- numero tre (1 + 1 + 1 = 3), notazione XXX- il numero trenta (10 + 10 + 10 = 30), ecc. Per scrivere i numeri valgono le seguenti regole.

1. Se il numero inferiore è Dopo più grande, quindi viene aggiunto a quello più grande: VII- numero sette (5 + 2 = 5 + 1 + 1 = 7), XVII- numero diciassette (10 + 7 = 10 + 5 + 1 + 1 = 17), MCL- il numero millecentocinquanta (1000 + 100 + 50 = 1150).
2. Se il numero inferiore è Prima più grande, allora viene sottratto dal più grande: IX- numero nove (9 = 10 - 1), L.M.- numero novecentocinquanta (1000 - 50 = 950).

Per scrivere numeri grandi, devi usare (inventare) nuovi simboli: i numeri. Allo stesso tempo, registrare i numeri risulta complicato ed è molto difficile eseguire calcoli con i numeri romani. Pertanto, nei documenti romani, l'anno del lancio del primo satellite artificiale della Terra (1957) ha la forma MCMLVII .

Blocco 1. 8. Carta perforata

Lettura dei numeri naturali

Queste attività vengono controllate utilizzando una mappa con cerchi. Spieghiamo la sua applicazione. Dopo aver completato tutti i compiti e trovato le risposte corrette (sono indicate dalle lettere A, B, C, ecc.), posiziona un foglio di carta trasparente sulla mappa. Usa i segni "X" per contrassegnare le risposte corrette, così come il segno corrispondente "+". Quindi adagiare il foglio trasparente sulla pagina in modo che i crocini di registrazione siano allineati. Se tutti i segni "X" si trovano nei cerchi grigi in questa pagina, le attività sono state completate correttamente.

1.9. Ordine di lettura dei numeri naturali

Quando leggi un numero naturale, procedi come segue.

1. Dividi mentalmente il numero in terzine (classi) da destra a sinistra, dalla fine del numero.

1. Partendo dalla classe junior, da destra a sinistra (dalla fine del numero) scrivi i nomi delle classi: unità, migliaia, milioni, miliardi, trilioni, quadrilioni, quintilioni.
2. Leggono il numero a partire dal liceo. In questo caso vengono richiamati il ​​numero di unità di bit e il nome della classe.
3. Se un bit contiene uno zero (il bit è vuoto), non viene chiamato. Se tutte e tre le cifre della classe denominata sono zero (le cifre sono vuote), questa classe non viene chiamata.

Leggiamo (nome) il numero scritto nella tabella (vedi §1), secondo i passaggi 1 - 4. Dividiamo mentalmente il numero 38001102987000128425 in classi da destra a sinistra: 038 001 102 987 000 128 425. Indichiamo i nomi dei classifica in questo numero, partendo dalla fine i suoi record: unità, migliaia, milioni, miliardi, trilioni, quadrilioni, quintilioni. Ora puoi leggere il numero, iniziando dalla classe senior. Nominiamo numeri a tre cifre, due cifre e una cifra, aggiungendo il nome della classe corrispondente. Non nominiamo classi vuote. Otteniamo il seguente numero:

• 038 - trentotto quintilioni
• 001 - un quadrilione
• 102 - centodue trilioni
• 987 - novecentottantasette miliardi
• 000 - non nominiamo (non leggiamo)
• 128 - centoventottomila
• 425 - quattrocentoventicinque

Di conseguenza, leggiamo il numero naturale 38 001 102 987 000 128 425 come segue: "trentotto quintilioni un quadrilione centodue trilioni novecentottantasette miliarditicinque."

1.9. L'ordine di scrittura dei numeri naturali

I numeri naturali si scrivono nel seguente ordine.

1. Annota tre cifre di ciascuna classe, iniziando dalla classe più alta fino alle unità. In questo caso, per la classe senior possono esserci due o una cifra.
2. Se la classe o categoria non ha un nome, nelle categorie corrispondenti verranno scritti degli zeri.

Ad esempio, numero venticinque milioni trecentodue scritto nella forma: 25 000 302 (la classe delle migliaia non ha un nome, quindi tutte le cifre della classe delle migliaia sono scritte con zeri).

1.10. Rappresentazione dei numeri naturali come somma di termini numerici

Facciamo un esempio: 7.563.429 è la notazione decimale di un numero sette milioniocentoventinove. Questo numero contiene sette milioni, cinquecentomila, sei diecimila, tremila, quattrocento, due decine e nove unità. Può essere rappresentato come la somma: 7.563.429 = 7.000.000 + 500.000 + 60.000 + + 3.000 + 400 + 20 + 9. Questa notazione è chiamata rappresentazione di un numero naturale come somma di termini numerici.

Blocco 1.11. giochiamo

Tesori dei sotterranei

Sul campo da gioco c'è un disegno della fiaba di Kipling "Mowgli". Cinque scrigni hanno lucchetti. Per aprirli, è necessario risolvere i problemi. Allo stesso tempo, aprendo una cassa di legno, ottieni un punto. Aprire uno scrigno di latta ti dà due punti, uno scrigno di rame ottiene tre punti, uno scrigno d'argento ottiene quattro punti e uno scrigno d'oro ottiene cinque punti. Vince chi apre tutti i forzieri più velocemente. Lo stesso gioco può essere giocato su un computer.

1. Scrigno di legno

Scopri quanti soldi (in migliaia di rubli) ci sono in questa cassa. Per fare ciò, devi trovare il numero totale delle unità con la cifra più bassa della classe dei milioni per il numero: 125308453231.

1. Cassapanca in latta

Scopri quanti soldi (in migliaia di rubli) ci sono in questa cassa. Per fare ciò, nel numero 12530845323, trova il numero delle unità con la cifra più bassa della classe delle unità e il numero delle unità con la cifra più bassa della classe dei milioni. Quindi trova la somma di questi numeri e aggiungi il numero nelle decine di milioni a destra.

1. Cassapanca in rame

Per trovare il denaro in questo forziere (in migliaia di rubli), è necessario trovare nel numero 751305432198203 il numero delle unità con la cifra più bassa nella classe dei trilioni e il numero delle unità con la cifra più bassa nella classe dei miliardi. Quindi trova la somma di questi numeri e scrivi a destra i numeri naturali della classe di unità di questo numero nell'ordine della loro posizione.

1. Cassapanca d'argento

Il denaro in questo scrigno (in milioni di rubli) sarà indicato dalla somma di due numeri: il numero delle unità con la cifra più bassa della classe delle migliaia e le unità con la cifra media della classe dei miliardi per il numero 481534185491502.

1. Petto d'oro

Viene fornito il numero 800123456789123456789.Se moltiplichiamo i numeri nelle cifre più alte di tutte le classi di questo numero, otteniamo i soldi di questa cassa in un milione di rubli.

Blocco 1.12. Incontro

Scrivere i numeri naturali. Rappresentazione dei numeri naturali come somma di termini numerici

Per ogni attività nella colonna di sinistra, seleziona una soluzione dalla colonna di destra. Scrivi la risposta nella forma: 1a; 2g; 3b…

	Scrivi il numero in numeri: cinque milioni e venticinquemila
	Scrivi il numero in numeri: cinque miliardi e venticinque milioni
	Scrivi il numero in numeri: cinque trilioni e venticinque
	Scrivi il numero in numeri:emilasettecentosettantasette
	Scrivi il numero in numeri: settantasette trilioni
	Scrivi il numero in numeri:ttantasettemilasette
	Scrivi il numero in numeri: centoventitre miliardi quattrocentocinquantasei milioni settecentottantanovemila
	Scrivi il numero in numeri: centoventitre milioniecentottantanove
	Scrivi il numero in numeri: tre miliardi e undici
	Scrivi il numero in numeri: tre miliardi undici milioni

opzione 2

	nquemilioniduecentonovantottomilatrecentoquarantuno		100000000 + 1000000 + 10000 + 100 + 1
	Presentare il numero come somma di termini numerici: trecentoventuno milioni quarantuno		30000000000 + 2000000000 + 100000000 + 70000000 + 5000000 + 200000 + 90000 + 8000 + 300 + 40 + 1
	Presentare il numero come somma di termini numerici: 321000175298341
	Presentare il numero come somma di termini numerici: 101010101
	Presentare il numero come somma di termini numerici: 11111		300000000 + 20000000 + 1000000 +
	5000000 + 300000 + 20000 + 1000
	Scrivi in ​​notazione decimale il numero presentato come somma di termini numerici: 5000000 + 300 + 20 + 1		30000000000000 + 2000000000000 + 1000000000000 + 100000000 + 70000000 + 5000000 + 200000 + 90000 + 8000 + 300 + 40 + 1
	Scrivi in ​​notazione decimale il numero presentato come somma di termini numerici: 10000000000 + 2000000000 + 100000 + 10 + 9
	Scrivi in ​​notazione decimale il numero presentato come somma di termini numerici: 10000000000 + 2000000000 + 100000000 + 10000000 + 9000000
	Scrivi in ​​notazione decimale il numero presentato come somma di termini numerici: 9000000000000 + 9000000000 + 9000000 + 9000 + 9		10000 + 1000 + 100 + 10 + 1

Blocco 1.13. Prova delle sfaccettature

Il nome del test deriva dalla parola “occhio composto dell’insetto”. Questo è un occhio complesso costituito da singoli "ocelli". Le attività di test sfaccettato sono formate da singoli elementi indicati da numeri. In genere, i test delle sfaccettature contengono un gran numero di attività. Ma in questo test ci sono solo quattro compiti, che però sono composti da un gran numero di elementi. Questo è progettato per insegnarti come "assemblare" i problemi dei test. Se riesci a crearli, puoi facilmente gestire altri test sulle faccette.

Spieghiamo come sono composte le attività utilizzando l'esempio della terza attività. È composto da elementi di prova numerati: 1, 4, 7, 11, 1, 5, 7, 9, 10, 16, 17, 22, 21, 25

« Se» 1) prendere i numeri (cifra) dalla tabella; 4) 7; 7) inserirlo in una categoria; 11) miliardi; 1) prendi un numero dalla tabella; 5) 8; 7) posizionarlo in categorie; 9) decine di milioni; 10) centinaia di milioni; 16) centinaia di migliaia; 17) decine di migliaia; 22) Inserisci i numeri 9 e 6 nelle posizioni delle migliaia e delle centinaia. 21) riempire i bit rimanenti con zeri; " QUELLO» 26) otteniamo un numero pari al tempo (periodo) di rivoluzione del pianeta Plutone attorno al Sole in secondi (s); " Questo numero è uguale a": 7880889600 pag. Nelle risposte è indicato dalla lettera "V".

Quando risolvi i problemi, usa una matita per scrivere i numeri nelle celle della tabella.

Prova delle sfaccettature. Componi un numero

La tabella contiene i numeri:

Se

1) prendi il/i numero/i dalla tabella:

2) 4; 3) 5; 4) 7; 5) 8; 6) 9;

7) inserire questa/e cifra/e nella/e cifra/e;

8) centinaia di quadrilioni e decine di quadrilioni;

9) decine di milioni;

10) centinaia di milioni;

11) miliardi;

12) quintilioni;

13) decine di quintilioni;

14) centinaia di quintilioni;

15) trilioni;

16) centinaia di migliaia;

17) decine di migliaia;

18) riempire le classi con esso (loro);

19) quintilioni;

20) miliardi;

21) riempire i bit rimanenti con zeri;

22) posizionare i numeri 9 e 6 nelle cifre delle migliaia e delle centinaia;

23) otteniamo un numero pari alla massa della Terra in decine di tonnellate;

24) otteniamo un numero approssimativamente uguale al volume della Terra in metri cubi;

25) otteniamo un numero pari alla distanza (in metri) dal Sole al pianeta più lontano del sistema solare, Plutone;

26) otteniamo un numero pari al tempo (periodo) di rivoluzione del pianeta Plutone attorno al Sole in secondi (s);

Questo numero è uguale a:

a) 5929000000000

b) 9999900000000000000000

d) 5980000000000000000000

Risolvere problemi:

1, 3, 6, 5, 18, 19, 21, 23

1, 6, 7, 14, 13, 12, 8, 21, 24

1, 4, 7, 11, 1, 5, 7, 10, 9, 16, 17, 22, 21, 26

1, 3, 7, 15, 1, 6, 2, 6, 18, 20, 21, 25

Risposte

1, 3, 6, 5, 18, 19, 21, 23 - g

1, 6, 7, 14, 13, 12, 8, 21, 24 -b

1, 4, 7, 11, 1, 5, 7, 10, 9, 16, 17, 22, 21, 26 - pollici

1, 3, 7, 15, 1, 6, 2, 6, 18, 20, 21, 25 - a

In matematica esistono diversi insiemi di numeri: reali, complessi, interi, razionali, irrazionali,... Nel nostro Vita di ogni giorno Usiamo molto spesso i numeri naturali, poiché li incontriamo durante il conteggio e durante la ricerca, designando il numero di oggetti.

In contatto con

Quali numeri sono chiamati numeri naturali?

Da dieci cifre puoi scrivere assolutamente qualsiasi somma esistente di classi e gradi. I valori naturali sono considerati quelli che vengono utilizzati:

• Quando si contano oggetti (primo, secondo, terzo, ... quinto, ... decimo).
• Quando si indica il numero di elementi (uno, due, tre...)

I valori N sono sempre interi e positivi. Non esiste N più grande perché l'insieme dei valori interi è illimitato.

Attenzione! I numeri naturali si ottengono quando si contano gli oggetti o quando si indica la loro quantità.

Qualsiasi numero può essere scomposto e presentato sotto forma di cifre, ad esempio: 8.346.809=8 milioni+346mila+809 unità.

Imposta N

L'insieme N è nell'insieme reale, intero e positivo. Nel diagramma degli insiemi essi si troverebbero l'uno nell'altro, poiché l'insieme degli insiemi naturali ne fa parte.

L'insieme dei numeri naturali è indicato con la lettera N. Questo insieme ha un inizio, ma non ha fine.

Esiste anche un insieme esteso N, dove è incluso lo zero.

Numero naturale più piccolo

Nella maggior parte delle scuole di matematica, il valore più piccolo di N è considerata un'unità, poiché l'assenza di oggetti è considerata vuota.

Ma nelle scuole matematiche straniere, ad esempio in quella francese, è considerato naturale. La presenza dello zero nella serie facilita la dimostrazione alcuni teoremi.

Una serie di valori N che comprende lo zero si dice estesa e si indica con il simbolo N0 (indice zero).

Serie di numeri naturali

Una riga N è una sequenza di tutti gli N gruppi di cifre. Questa sequenza non ha fine.

La particolarità della serie naturale è che il numero successivo differirà di uno dal precedente, cioè aumenterà. Ma i significati non può essere negativo.

Attenzione! Per comodità di conteggio, ci sono classi e categorie:

• Unità (1, 2, 3),
• Decine (10, 20, 30),
• Centinaia (100, 200, 300),
• Migliaia (1000, 2000, 3000),
• Decine di migliaia (30.000),
• Centinaia di migliaia (800.000),
• Milioni (4000000), ecc.

Tutti N

Tutti gli N appartengono all'insieme dei valori reali, interi, non negativi. Sono loro parte integrale.

Questi valori vanno all'infinito, possono appartenere alle classi di milioni, miliardi, quintilioni, ecc.

Per esempio:

• Cinque mele, tre gattini,
• Dieci rubli, trenta matite,
• Cento chilogrammi, trecento libri,
• Un milione di stelle, tre milioni di persone, ecc.

Sequenza in N

In diverse scuole matematiche si possono trovare due intervalli a cui appartiene la sequenza N:

da zero a più infinito, estremi compresi, e da uno a più infinito, estremi compresi, cioè tutto risposte complete positive.

N gruppi di cifre possono essere pari o dispari. Consideriamo il concetto di stranezza.

Dispari (qualsiasi numero dispari termina con i numeri 1, 3, 5, 7, 9.) con due ha resto. Ad esempio, 7:2=3,5, 11:2=5,5, 23:2=11,5.

Cosa significa anche N?

Qualsiasi somma pari di classi termina con numeri: 0, 2, 4, 6, 8. Quando anche N viene diviso per 2, non ci sarà resto, cioè il risultato sarà l'intera risposta. Ad esempio, 50:2=25, 100:2=50, 3456:2=1728.

Importante! Una serie numerica di N non può essere costituita solo da valori pari o dispari, poiché devono alternarsi: il pari è sempre seguito dal dispari, seguito ancora dal pari, ecc.

ProprietàN

Come tutti gli altri insiemi, N ha le sue proprietà speciali. Considera le proprietà della serie N (non estesa).

• Il valore che è il più piccolo e che non ne segue nessun altro è uno.
• N sono una sequenza, cioè un valore naturale ne segue un altro(tranne uno: è il primo).
• Quando eseguiamo operazioni di calcolo su N somme di cifre e classi (addizione, moltiplicazione), allora la risposta risulta sempre naturale Senso.
• Permutazione e combinazione possono essere utilizzate nei calcoli.
• Ogni valore successivo non può essere inferiore al precedente. Anche nella serie N varrà la seguente legge: se il numero A è minore di B, allora nella serie numerica ci sarà sempre un C per il quale vale l'uguaglianza: A+C=B.
• Se prendiamo due espressioni naturali, ad esempio A e B, per loro sarà vera una delle espressioni: A = B, A è maggiore di B, A è minore di B.
• Se A è inferiore a B e B è inferiore a C, ne consegue che che A è minore di C.
• Se A è minore di B, ne consegue che: se aggiungiamo loro la stessa espressione (C), allora A + C è minore di B + C. È anche vero che se questi valori vengono moltiplicati per C, allora AC è minore di AB.
• Se B è maggiore di A, ma minore di C, allora è vero: B-A è minore di C-A.

Attenzione! Tutte le disuguaglianze di cui sopra sono valide anche nella direzione opposta.

Come si chiamano le componenti della moltiplicazione?

In molti problemi semplici e persino complessi, trovare la risposta dipende dalle capacità degli scolari.

Per moltiplicare rapidamente e correttamente ed essere in grado di risolvere problemi inversi, è necessario conoscere le componenti della moltiplicazione.

15. 10=150. In questa espressione ci sono 15 e 10 sono moltiplicatori e 150 è un prodotto.

La moltiplicazione ha proprietà necessarie per risolvere problemi, equazioni e disuguaglianze:

• La riorganizzazione dei fattori non cambierà il prodotto finale.
• Per trovare un fattore sconosciuto, è necessario dividere il prodotto per un fattore noto (vero per tutti i fattori).

Ad esempio: 15 . X=150. Dividiamo il prodotto per un fattore noto. 150:15=10. Facciamo un controllo. 15 . 10=150. Secondo questo principio, addirittura decidono equazioni lineari complesse(per semplificarli).

Importante! Un prodotto può essere costituito da più di due soli fattori. Ad esempio: 840=2 . 5. 7. 3. 4

Cosa sono i numeri naturali in matematica?

Luoghi e classi dei numeri naturali

Conclusione

Riassumiamo. N viene utilizzato quando si conta o si indica il numero di articoli. La serie degli insiemi naturali di numeri è infinita, ma include solo somme intere e positive di cifre e classi. Per farlo è necessaria anche la moltiplicazione contare gli oggetti, nonché per risolvere problemi, equazioni e varie disuguaglianze.

La matematica emerse dalla filosofia generale intorno al VI secolo a.C. e., e da quel momento iniziò la sua marcia vittoriosa intorno al mondo. Ogni fase di sviluppo ha introdotto qualcosa di nuovo: il conteggio elementare si è evoluto, trasformato in calcolo differenziale e integrale, sono passati i secoli, le formule sono diventate sempre più confuse e è arrivato il momento in cui "è iniziata la matematica più complessa - tutti i numeri sono scomparsi da essa". Ma quale era la base?

L'inizio del tempo

I numeri naturali apparvero insieme alle prime operazioni matematiche. Una spina dorsale, due spine, tre spine... Sono apparse grazie agli scienziati indiani che hanno sviluppato la prima posizionale

La parola “posizionalità” significa che la posizione di ciascuna cifra in un numero è rigorosamente definita e corrisponde al suo rango. Ad esempio, i numeri 784 e 487 sono gli stessi numeri, ma i numeri non sono equivalenti, poiché il primo comprende 7 centinaia, mentre il secondo solo 4. L'innovazione indiana fu ripresa dagli arabi, che portarono i numeri nella forma che ora sappiamo.

Nei tempi antichi, ai numeri veniva dato un significato mistico; Pitagora credeva che il numero fosse alla base della creazione del mondo insieme agli elementi di base: fuoco, acqua, terra, aria. Se consideriamo tutto solo dal lato matematico, allora cos'è un numero naturale? Il campo dei numeri naturali si indica con N ed è una serie infinita di numeri interi e positivi: 1, 2, 3, … + ∞. Lo zero è escluso. Utilizzato principalmente per contare gli articoli e indicare l'ordine.

Cosa c'è in matematica? Gli assiomi di Peano

Il campo N è quello fondamentale su cui si basa la matematica elementare. Nel tempo, campi di numeri interi, razionali,

Il lavoro del matematico italiano Giuseppe Peano rese possibile l'ulteriore strutturazione dell'aritmetica, ne raggiunse la formalità e preparò la strada per ulteriori conclusioni che andarono oltre l'area del campo N.

Cos'è un numero naturale è stato chiarito in precedenza in linguaggio semplice; di seguito considereremo la definizione matematica basata sugli assiomi di Peano.

• Uno è considerato un numero naturale.
• Il numero che segue un numero naturale è un numero naturale.
• Non esiste un numero naturale prima dell'uno.
• Se il numero b segue sia il numero c che il numero d, allora c=d.
• Un assioma di induzione, che a sua volta mostra cos'è un numero naturale: se un'affermazione che dipende da un parametro è vera per il numero 1, allora assumiamo che funzioni anche per il numero n dal campo dei numeri naturali N. Quindi l'affermazione vale anche per n =1 dal campo dei numeri naturali N.

Operazioni di base per il campo dei numeri naturali

Poiché il campo N è stato il primo per i calcoli matematici, ad esso appartengono sia i domini di definizione che gli intervalli di valori di una serie di operazioni sottostanti. Sono chiusi e non. La differenza principale è che è garantito che le operazioni chiuse lascino il risultato all'interno dell'insieme N, indipendentemente dai numeri coinvolti. È sufficiente che siano naturali. Il risultato di altre interazioni numeriche non è più così chiaro e dipende direttamente dal tipo di numeri coinvolti nell'espressione, poiché potrebbe contraddire la definizione principale. Quindi, operazioni chiuse:

• addizione - x + y = z, dove x, y, z sono inclusi nel campo N;
• moltiplicazione - x * y = z, dove x, y, z sono inclusi nel campo N;
• esponenziazione - x y, dove x, y sono inclusi nel campo N.

Le restanti operazioni, il cui risultato potrebbe non esistere nel contesto della definizione di "cos'è un numero naturale", sono le seguenti:

Proprietà dei numeri appartenenti al campo N

Tutti gli ulteriori ragionamenti matematici si baseranno sulle seguenti proprietà, le più banali, ma non per questo meno importanti.

• La proprietà commutativa dell’addizione è x + y = y + x, dove i numeri x, y sono compresi nel campo N. Oppure il noto “la somma non cambia cambiando le posizioni dei termini”.
• La proprietà commutativa della moltiplicazione è x * y = y * x, dove i numeri x, y sono inclusi nel campo N.
• La proprietà combinatoria dell'addizione è (x + y) + z = x + (y + z), dove x, y, z sono inclusi nel campo N.
• La proprietà corrispondente della moltiplicazione è (x * y) * z = x * (y * z), dove i numeri x, y, z sono inclusi nel campo N.
• proprietà distributiva - x (y + z) = x * y + x * z, dove i numeri x, y, z sono inclusi nel campo N.

Tavola pitagorica

Uno dei primi passi verso la conoscenza da parte degli studenti dell’intera struttura della matematica elementare dopo che hanno capito da soli quali numeri sono chiamati numeri naturali è la tavola pitagorica. Può essere considerato non solo dal punto di vista scientifico, ma anche come un monumento scientifico di grande valore.

Questa tavola pitagorica ha subito diverse modifiche nel corso del tempo: è stato eliminato lo zero, e i numeri da 1 a 10 si rappresentano se stessi, senza tenere conto degli ordini (centinaia, migliaia...). È una tabella in cui le intestazioni delle righe e delle colonne sono numeri e il contenuto delle celle in cui si intersecano è uguale al loro prodotto.

Nella pratica dell'insegnamento negli ultimi decenni, è nata la necessità di memorizzare la tavola pitagorica “in ordine”, cioè la memorizzazione è venuta prima. La moltiplicazione per 1 è stata esclusa perché il risultato era un moltiplicatore pari o superiore a 1. Nel frattempo, nella tabella ad occhio nudo puoi notare uno schema: il prodotto dei numeri aumenta di un passo, che è uguale al titolo della riga. Quindi, il secondo fattore ci mostra quante volte dobbiamo assumere il primo per ottenere il prodotto desiderato. Questo sistema è molto più conveniente di quello praticato nel Medioevo: pur capendo cos'è un numero naturale e quanto sia banale, le persone riuscivano a complicare il conteggio quotidiano utilizzando un sistema basato sulle potenze di due.

Sottoinsieme come culla della matematica

Al momento, il campo dei numeri naturali N è considerato solo come uno dei sottoinsiemi dei numeri complessi, ma ciò non li rende meno preziosi nella scienza. Il numero naturale è la prima cosa che un bambino impara studiando se stesso e il mondo che lo circonda. Un dito, due dita... Grazie ad esso, una persona sviluppa il pensiero logico, così come la capacità di determinare la causa e dedurre l'effetto, aprendo la strada a grandi scoperte.

I numeri naturali sono uno dei concetti matematici più antichi.

In un lontano passato, le persone non conoscevano i numeri e quando avevano bisogno di contare oggetti (animali, pesci, ecc.), lo facevano diversamente da adesso.

Il numero di oggetti è stato confrontato con parti del corpo, ad esempio, con le dita di una mano, e hanno detto: "Ho tante noci quante sono le dita della mia mano".

Nel corso del tempo, le persone si sono rese conto che cinque noci, cinque capre e cinque lepri hanno una proprietà comune: il loro numero è cinque.

Ricordare!

Numeri interi- questi sono numeri, a partire da 1, ottenuti contando gli oggetti.

1, 2, 3, 4, 5…

Numero naturale più piccolo — 1 .

Numero naturale più grande non esiste.

Durante il conteggio, il numero zero non viene utilizzato. Pertanto, lo zero non è considerato un numero naturale.

Le persone hanno imparato a scrivere i numeri molto più tardi che a contare. Prima di tutto, iniziarono a raffigurarne uno con un bastoncino, poi con due bastoncini - il numero 2, con tre - il numero 3.

| — 1, || — 2, ||| — 3, ||||| — 5 …

Quindi apparvero segni speciali per designare i numeri, i predecessori dei numeri moderni. I numeri che usiamo per scrivere i numeri hanno avuto origine in India circa 1.500 anni fa. Gli arabi li hanno portati in Europa, motivo per cui vengono chiamati Numeri arabi.

Ci sono dieci numeri in totale: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Usando questi numeri puoi scrivere qualsiasi numero naturale.

Ricordare!

Serie naturaliè una successione di tutti i numeri naturali:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …

Nella serie naturale ogni numero è maggiore di 1 rispetto al precedente.

La serie naturale è infinita: non esiste alcun numero naturale massimo.

Il sistema di conteggio che utilizziamo si chiama posizionale decimale.

Decimale perché 10 unità di ciascuna cifra formano 1 unità della cifra più significativa. Posizionale perché il significato di una cifra dipende dalla sua posizione nel record numerico, cioè dalla cifra in cui è scritta.

Importante!

Le classi che seguono il miliardo prendono il nome dei numeri latini. Ogni unità successiva ne contiene mille precedenti.

• 1.000 miliardi = 1.000.000.000.000 = 1 trilione ("tre" in latino significa "tre")
• 1.000 trilioni = 1.000.000.000.000.000 = 1 quadrilione (“quadra” in latino significa “quattro”)
• 1.000 quadrilioni = 1.000.000.000.000.000.000 = 1 quintilione (“quinta” in latino significa “cinque”)

Tuttavia, i fisici hanno trovato un numero che supera il numero di tutti gli atomi (le particelle più piccole della materia) nell'intero Universo.

Questo numero ha ricevuto un nome speciale: googol. Googol è un numero con 100 zeri.