Cosa sono gli autovettori e gli autovalori. Autovalori (numeri) e autovettori.Esempi di soluzioni

Come inserire formule matematiche su un sito web?

Se mai avessi bisogno di aggiungere una o due formule matematiche a una pagina web, il modo più semplice per farlo è quello descritto nell'articolo: le formule matematiche vengono facilmente inserite nel sito sotto forma di immagini generate automaticamente da Wolfram Alpha . Oltre alla semplicità, questo metodo universale aiuterà a migliorare la visibilità del sito nei motori di ricerca. Funziona da molto tempo (e, penso, funzionerà per sempre), ma è già moralmente obsoleto.

Se utilizzi regolarmente formule matematiche sul tuo sito, ti consiglio di utilizzare MathJax, una speciale libreria JavaScript che visualizza la notazione matematica nei browser Web utilizzando il markup MathML, LaTeX o ASCIIMathML.

Esistono due modi per iniziare a utilizzare MathJax: (1) utilizzando un semplice codice, puoi connettere rapidamente uno script MathJax al tuo sito web, che verrà caricato automaticamente da un server remoto al momento giusto (elenco dei server); (2) scarica lo script MathJax da un server remoto sul tuo server e collegalo a tutte le pagine del tuo sito. Il secondo metodo, più complesso e dispendioso in termini di tempo, accelererà il caricamento delle pagine del tuo sito e se il server MathJax principale diventa temporaneamente non disponibile per qualche motivo, ciò non influenzerà in alcun modo il tuo sito. Nonostante questi vantaggi ho scelto il primo metodo in quanto è più semplice, veloce e non richiede competenze tecniche. Segui il mio esempio e in soli 5 minuti potrai utilizzare tutte le funzionalità di MathJax sul tuo sito.

Puoi connettere lo script della libreria MathJax da un server remoto utilizzando due opzioni di codice prese dal sito web principale di MathJax o dalla pagina della documentazione:

Una di queste opzioni di codice deve essere copiata e incollata nel codice della tua pagina web, preferibilmente tra i tag e/o immediatamente dopo il tag. Secondo la prima opzione, MathJax si carica più velocemente e rallenta meno la pagina. Ma la seconda opzione monitora e carica automaticamente le ultime versioni di MathJax. Se inserisci il primo codice, sarà necessario aggiornarlo periodicamente. Se inserisci il secondo codice, le pagine si caricheranno più lentamente, ma non avrai bisogno di monitorare costantemente gli aggiornamenti di MathJax.

Il modo più semplice per connettere MathJax è in Blogger o WordPress: nel pannello di controllo del sito, aggiungi un widget progettato per inserire codice JavaScript di terze parti, copia al suo interno la prima o la seconda versione del codice di download presentato sopra e posiziona il widget più vicino all'inizio del modello (a proposito, questo non è affatto necessario, poiché lo script MathJax viene caricato in modo asincrono). È tutto. Ora impara la sintassi del markup di MathML, LaTeX e ASCIIMathML e sei pronto per inserire formule matematiche nelle pagine web del tuo sito.

Qualsiasi frattale è costruito secondo una determinata regola, che viene applicata costantemente un numero illimitato di volte. Ciascuno di questi momenti è chiamato iterazione.

L'algoritmo iterativo per costruire una spugna di Menger è abbastanza semplice: il cubo originale con lato 1 viene diviso da piani paralleli alle sue facce in 27 cubi uguali. Da esso vengono rimossi un cubo centrale e 6 cubi adiacenti ad esso lungo le facce. Il risultato è un set composto dai restanti 20 cubi più piccoli. Facendo lo stesso con ciascuno di questi cubi, otteniamo un set composto da 400 cubi più piccoli. Continuando questo processo all'infinito, otteniamo una spugna di Menger.

SISTEMA DI EQUAZIONI LINEARI OMOGENEE

Un sistema di equazioni lineari omogenee è un sistema della forma

È chiaro che in questo caso , Perché tutti gli elementi di una delle colonne in questi determinanti sono uguali a zero.

Poiché le incognite si trovano secondo le formule , allora nel caso in cui Δ ≠ 0, il sistema ha un'unica soluzione nulla X = sì = z= 0. Tuttavia, in molti problemi la domanda interessante è se un sistema omogeneo abbia soluzioni diverse da zero.

Teorema. Affinché un sistema di equazioni lineari omogenee abbia soluzione diversa da zero è necessario e sufficiente che Δ ≠ 0.

Quindi, se il determinante Δ ≠ 0, allora il sistema ha un'unica soluzione. Se Δ ≠ 0, allora il sistema di equazioni lineari omogenee ha un numero infinito di soluzioni.

Esempi.

Autovettori e autovalori di una matrice

Sia data una matrice quadrata , X– qualche colonna-matrice, la cui altezza coincide con l'ordine della matrice UN. .

In molti problemi dobbiamo considerare l'equazione per X

dove λ è un certo numero. È chiaro che per ogni λ questa equazione ha soluzione zero.

Viene chiamato il numero λ per il quale questa equazione ha soluzioni diverse da zero autovalore matrici UN, UN X per tale si chiama λ autovettore matrici UN.

Troviamo l'autovettore della matrice UN. Perché il E∙X = X, allora l'equazione della matrice può essere riscritta come O . In forma estesa, questa equazione può essere riscritta come un sistema di equazioni lineari. Veramente .

E quindi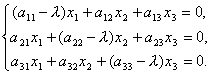

Quindi, abbiamo ottenuto un sistema di equazioni lineari omogenee per determinare le coordinate x1, x2, x3 vettore X. Affinché un sistema abbia soluzioni diverse da zero è necessario e sufficiente che il determinante del sistema sia uguale a zero, cioè

Questa è un'equazione di 3° grado per λ. È chiamato equazione caratteristica matrici UN e serve a determinare gli autovalori di λ.

Ogni autovalore λ corrisponde ad un autovettore X, le cui coordinate sono determinate dal sistema al corrispondente valore di λ.

Esempi.

ALGEBRA VETTORIALE. IL CONCETTO DI VETTORE

Quando si studiano vari rami della fisica, ci sono quantità che vengono completamente determinate specificando i loro valori numerici, ad esempio lunghezza, area, massa, temperatura, ecc. Tali quantità sono chiamate scalari. Oltre ad essi però esistono anche delle quantità, per determinare le quali, oltre al valore numerico, è necessario conoscere anche la loro direzione nello spazio, ad esempio la forza che agisce sul corpo, la velocità e l'accelerazione del corpo corpo quando si muove nello spazio, l'intensità del campo magnetico in un dato punto dello spazio, ecc. Tali quantità sono chiamate quantità vettoriali.

Introduciamo una definizione rigorosa.

Segmento diretto Chiamiamo un segmento, rispetto alle cui estremità è noto quale di essi è il primo e quale è il secondo.

Vettore chiamato segmento diretto avente una certa lunghezza, cioè Questo è un segmento di una certa lunghezza, in cui uno dei punti che lo limitano è preso come inizio e il secondo come fine. Se UN– l'inizio del vettore, Bè la sua fine, allora il vettore è indicato con il simbolo; inoltre, il vettore è spesso indicato con una singola lettera. Nella figura il vettore è indicato da un segmento e la sua direzione da una freccia.

Modulo O lunghezza Un vettore è chiamato lunghezza del segmento orientato che lo definisce. Indicato con || o ||.

Includeremo come vettori anche il cosiddetto vettore zero, il cui inizio e fine coincidono. È designato. Il vettore zero non ha una direzione specifica e il suo modulo è zero ||=0.

Si chiamano vettori collineare, se si trovano sulla stessa linea o su linee parallele. Inoltre, se i vettori e sono nella stessa direzione, scriveremo , opposto.

Si chiamano vettori posti su rette parallele allo stesso piano Complanare.

I due vettori vengono chiamati pari, se sono collineari, hanno la stessa direzione e sono uguali in lunghezza. In questo caso scrivono.

Dalla definizione di uguaglianza dei vettori segue che un vettore può essere trasportato parallelamente a se stesso, ponendo la sua origine in qualsiasi punto dello spazio.

Per esempio .

OPERAZIONI LINEARI SUI VETTORI

Moltiplicare un vettore per un numero.

Il prodotto di un vettore per il numero λ è un nuovo vettore tale che:

Il prodotto di un vettore e di un numero λ è indicato con .

Ad esempio, esiste un vettore diretto nella stessa direzione del vettore e avente una lunghezza pari alla metà del vettore.

L’operazione introdotta ha le seguenti proprietà:

Aggiunta di vettori.

Siano e due vettori arbitrari. Prendiamo un punto arbitrario O e costruire un vettore. Dopodiché dal punto UN mettiamo da parte il vettore. Viene chiamato il vettore che collega l'inizio del primo vettore con la fine del secondo quantità di questi vettori ed è indicato .

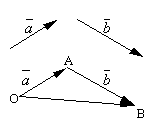
Viene chiamata la definizione formulata di addizione vettoriale regola del parallelogramma, poiché la stessa somma di vettori può essere ottenuta come segue. Rimandiamo il punto O vettori e. Costruiamo un parallelogramma su questi vettori OABC. Da vettori, quindi vettore, che è una diagonale di un parallelogramma disegnato dal vertice O, sarà ovviamente una somma di vettori.

È facile verificare le seguenti proprietà dell'addizione vettoriale.

Differenza vettoriale.

Viene chiamato un vettore collineare a un dato vettore, uguale in lunghezza e diretto in senso opposto opposto vettore per un vettore ed è indicato con . Il vettore opposto può essere considerato come il risultato della moltiplicazione del vettore per il numero λ = –1: .

Un autovettore di una matrice quadrata è quello che, moltiplicato per una determinata matrice, dà come risultato un vettore collineare. In parole semplici, quando una matrice viene moltiplicata per un autovettore, quest'ultimo rimane lo stesso, ma moltiplicato per un certo numero.

Definizione

Un autovettore è un vettore V diverso da zero che, moltiplicato per una matrice quadrata M, aumenta a sua volta di un numero λ. In notazione algebrica risulta:

M × V = λ × V,

dove λ è l'autovalore della matrice M.

Consideriamo un esempio numerico. Per facilitare la registrazione, i numeri nella matrice verranno separati da un punto e virgola. Prendiamo una matrice:

• M = 0; 4;
• 6; 10.

Moltiplichiamolo per un vettore colonna:

• V = -2;

Quando moltiplichiamo una matrice per un vettore colonna, otteniamo anche un vettore colonna. In linguaggio matematico rigoroso, la formula per moltiplicare una matrice 2 × 2 per un vettore colonna sarà simile a questa:

• M×V = M11×V11 + M12×V21;
• M21×V11 + M22×V21.

Con M11 si intende l'elemento della matrice M situato nella prima riga e nella prima colonna, e con M22 si intende l'elemento situato nella seconda riga e nella seconda colonna. Per la nostra matrice, questi elementi sono uguali a M11 = 0, M12 = 4, M21 = 6, M22 10. Per un vettore colonna, questi valori sono uguali a V11 = –2, V21 = 1. Secondo questa formula, otteniamo il seguente risultato del prodotto di una matrice quadrata per un vettore:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Per comodità, scriviamo il vettore colonna in una riga. Quindi, abbiamo moltiplicato la matrice quadrata per il vettore (-2; 1), ottenendo il vettore (4; -2). Ovviamente si tratta dello stesso vettore moltiplicato per λ = -2. Lambda in questo caso denota l'autovalore della matrice.

Un autovettore di una matrice è un vettore collineare, cioè un oggetto che non cambia la sua posizione nello spazio quando moltiplicato per una matrice. Il concetto di collinearità nell'algebra vettoriale è simile al termine di parallelismo in geometria. In un'interpretazione geometrica, i vettori collineari sono segmenti diretti paralleli di diversa lunghezza. Sin dai tempi di Euclide, sappiamo che una linea ha un numero infinito di linee parallele ad essa, quindi è logico supporre che ciascuna matrice abbia un numero infinito di autovettori.

Dall'esempio precedente è chiaro che gli autovettori possono essere (-8; 4), e (16; -8), e (32, -16). Questi sono tutti vettori collineari corrispondenti all'autovalore λ = -2. Moltiplicando la matrice originale per questi vettori, ci ritroveremo comunque con un vettore che differisce dall'originale di 2 volte. Ecco perché, quando si risolvono i problemi di ricerca di un autovettore, è necessario trovare solo oggetti vettoriali linearmente indipendenti. Molto spesso, per una matrice n × n, esiste un numero n di autovettori. La nostra calcolatrice è progettata per l'analisi di matrici quadrate del secondo ordine, quindi quasi sempre il risultato troverà due autovettori, tranne i casi in cui coincidono.

Nell'esempio precedente conoscevamo in anticipo l'autovettore della matrice originale e abbiamo determinato chiaramente il numero lambda. Tuttavia, in pratica, tutto avviene al contrario: prima si trovano gli autovalori e solo dopo gli autovettori.

Algoritmo risolutivo

Consideriamo nuovamente la matrice originale M e proviamo a trovare entrambi i suoi autovettori. Quindi la matrice è simile a:

• M = 0; 4;
• 6; 10.

Per prima cosa dobbiamo determinare l'autovalore λ, che richiede il calcolo del determinante della seguente matrice:

• (0 − λ); 4;
• 6; (10 − λ).

Questa matrice si ottiene sottraendo l'incognita λ dagli elementi sulla diagonale principale. Il determinante viene determinato utilizzando la formula standard:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Poiché il nostro vettore deve essere diverso da zero, accettiamo l'equazione risultante come dipendente linearmente e equiparamo il nostro determinante detA a zero.

(0 − λ) × (10 − λ) − 24 = 0

Apriamo le parentesi e otteniamo l'equazione caratteristica della matrice:

λ2 − 10λ − 24 = 0

Questa è un'equazione quadratica standard che deve essere risolta utilizzando un discriminante.

D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

La radice del discriminante è sqrt(D) = 14, quindi λ1 = -2, λ2 = 12. Ora per ogni valore lambda dobbiamo trovare l'autovettore. Esprimiamo i coefficienti del sistema per λ = -2.

• M − λ × E = 2; 4;
• 6; 12.

In questa formula, E è la matrice identità. Sulla base della matrice risultante, creiamo un sistema di equazioni lineari:

2x + 4y = 6x + 12y,

dove x e y sono gli elementi dell'autovettore.

Raccogliamo tutte le X a sinistra e tutte le Y a destra. Ovviamente - 4x = 8y. Dividi l'espressione per - 4 e ottieni x = –2y. Ora possiamo determinare il primo autovettore della matrice, prendendo qualsiasi valore delle incognite (ricordiamo l'infinito degli autovettori linearmente dipendenti). Prendiamo y = 1, quindi x = –2. Pertanto, il primo autovettore assomiglia a V1 = (–2; 1). Ritorna all'inizio dell'articolo. È stato questo oggetto vettoriale per cui abbiamo moltiplicato la matrice per dimostrare il concetto di autovettore.

Ora troviamo l'autovettore per λ = 12.

• M - λ × E = -12; 4
• 6; -2.

Creiamo lo stesso sistema di equazioni lineari;

• -12x + 4y = 6x − 2y
• -18x = -6a
• 3x = y.

Ora prendiamo x = 1, quindi y = 3. Pertanto, il secondo autovettore assomiglia a V2 = (1; 3). Moltiplicando la matrice originale per un dato vettore, il risultato sarà sempre lo stesso vettore moltiplicato per 12. Qui termina l'algoritmo di soluzione. Ora sai come determinare manualmente l'autovettore di una matrice.

• determinante;
• tracciare, cioè, la somma degli elementi sulla diagonale principale;
• rango, ovvero il numero massimo di righe/colonne linearmente indipendenti.

Il programma funziona secondo l'algoritmo di cui sopra, abbreviando il più possibile il processo di soluzione. È importante sottolineare che nel programma lambda è indicata con la lettera “c”. Consideriamo un esempio numerico.

Esempio di come funziona il programma

Proviamo a determinare gli autovettori per la seguente matrice:

• M = 5; 13;
• 4; 14.

Inseriamo questi valori nelle celle della calcolatrice e otteniamo la risposta nel seguente modulo:

• Grado della matrice: 2;
• Determinante della matrice: 18;
• Traccia della matrice: 19;
• Calcolo dell'autovettore: c 2 − 19.00c + 18.00 (equazione caratteristica);
• Calcolo dell'autovettore: 18 (primo valore lambda);
• Calcolo dell'autovettore: 1 (secondo valore lambda);
• Sistema di equazioni per il vettore 1: -13x1 + 13y1 = 4x1 − 4y1;
• Sistema di equazioni per il vettore 2: 4x1 + 13y1 = 4x1 + 13y1;
• Autovettore 1: (1; 1);
• Autovettore 2: (-3,25; 1).

Pertanto, abbiamo ottenuto due autovettori linearmente indipendenti.

Conclusione

L'algebra lineare e la geometria analitica sono materie standard per qualsiasi studente matricola di ingegneria. Il gran numero di vettori e matrici è terrificante ed è facile commettere errori in calcoli così complicati. Il nostro programma consentirà agli studenti di verificare i propri calcoli o di risolvere automaticamente il problema della ricerca di un autovettore. Ci sono altri calcolatori di algebra lineare nel nostro catalogo; usali nei tuoi studi o nel tuo lavoro.

Definizione 9.3. Vettore Xè detto autovettore della matrice UN, se esiste un tale numero λ, che vale l'uguaglianza: Ах = λх, cioè, il risultato dell'applicazione a X trasformazione lineare specificata dalla matrice UN, è la moltiplicazione di questo vettore per il numero λ . Il numero stesso λ è detto autovalore della matrice UN.

Sostituendo nelle formule (9.3) x` j = λx j , otteniamo un sistema di equazioni per determinare le coordinate dell'autovettore:

. (9.5)

Questo sistema lineare omogeneo avrà una soluzione non banale solo se il suo determinante principale è 0 (regola di Cramer). Scrivendo questa condizione nella forma:

otteniamo un'equazione per determinare gli autovalori λ , detta equazione caratteristica. Brevemente può essere rappresentato come segue:

| A-λE | = 0, (9.6)

poiché il suo lato sinistro contiene il determinante della matrice A-λE. Relativo polinomiale λ | A-λE| è detto polinomio caratteristico della matrice A.

Proprietà del polinomio caratteristico:

1) Il polinomio caratteristico di una trasformazione lineare non dipende dalla scelta della base. Prova. (vedi (9.4)), ma quindi, . Pertanto, non dipende dalla scelta della base. Ciò significa che | A-λE| non cambia quando si passa a una nuova base.

2) Se la matrice UN la trasformazione lineare è simmetrica (cioè e ij =a ji), allora tutte le radici dell'equazione caratteristica (9.6) sono numeri reali.

Proprietà degli autovalori e degli autovettori:

1) Se si sceglie una base dagli autovettori x1, x2, x3, corrispondenti agli autovalori λ1, λ2, λ3 matrici UN, allora in questa base la trasformazione lineare A ha una matrice di forma diagonale:

(9.7) La dimostrazione di questa proprietà segue dalla definizione di autovettori.

2) Se gli autovalori della trasformazione UN sono diversi, allora i loro autovettori corrispondenti sono linearmente indipendenti.

3) Se il polinomio caratteristico della matrice UN ha tre radici diverse, quindi in qualche base la matrice UN ha un aspetto diagonale.

Troviamo gli autovalori e gli autovettori della matrice. Creiamo un'equazione caratteristica: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³-7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Troviamo le coordinate degli autovettori corrispondenti a ciascun valore trovato λ. Dalla (9.5) segue che se X (1) ={x1,x2,x3) – corrispondente all'autovettore λ 1=-2, quindi

- un sistema cooperativo ma incerto. La sua soluzione può essere scritta nella forma X (1) ={UN,0,-UN), dove a è un numero qualsiasi. In particolare, se richiediamo che | X (1) |=1, X (1) =

Sostituzione nel sistema (9.5) λ 2 =3, otteniamo un sistema per determinare le coordinate del secondo autovettore - X (2) ={sì1, sì2, sì3}:

, Dove X (2) ={b,-b,b) oppure, purché | X (2) |=1, X (2) =

Per λ 3 = 6 trova l'autovettore X (3) ={z1, z2, z3}:

, X (3) ={C,2c,c) o nella versione normalizzata

x(3) = Lo si può notare X (1) X (2) = ab–ab= 0, X (1) X (3) = ac-ac= 0, X (2) X (3) = avanti Cristo- 2ac + ac= 0. Pertanto, gli autovettori di questa matrice sono ortogonali a coppie.

Lezione 10.

Forme quadratiche e loro connessione con matrici simmetriche. Proprietà degli autovettori e degli autovalori di una matrice simmetrica. Riduzione di una forma quadratica a forma canonica.

Definizione 10.1. Forma quadratica delle variabili reali x1, x2,…, xn si chiama polinomio di secondo grado in queste variabili che non contiene un termine libero e termini di primo grado.

Esempi di forme quadratiche:

(N = 2),

(N = 3). (10.1)

Ricordiamo la definizione di matrice simmetrica data nell'ultima lezione:

Definizione 10.2. Una matrice quadrata si dice simmetrica se, cioè, se gli elementi della matrice che sono simmetrici rispetto alla diagonale principale sono uguali.

Proprietà degli autovalori e degli autovettori di una matrice simmetrica:

1) Tutti gli autovalori di una matrice simmetrica sono reali.

Prova (per N = 2).

Lasciamo la matrice UN ha la forma: . Creiamo un'equazione caratteristica:

(10.2) Troviamo il discriminante:

Pertanto l’equazione ha solo radici reali.

2) Gli autovettori di una matrice simmetrica sono ortogonali.

Prova (per N= 2).

Le coordinate degli autovettori e devono soddisfare le equazioni.