Natural value. Natural Numbers - Basics

Numbers are an abstract concept. They are a quantitative characteristic of objects and can be real, rational, negative, integer and fractional, as well as natural.

The natural series is usually used when counting, in which quantity notations naturally arise. Acquaintance with counting begins in early childhood. What kid avoided funny rhymes that used elements of natural counting? "One, two, three, four, five... The bunny went out for a walk!" or "1, 2, 3, 4, 5, 6, 7, 8, 9, 10, the king decided to hang me..."

For any natural number, you can find another one greater than it. This set is usually denoted by the letter N and should be considered infinite in the direction of increase. But this set has a beginning - it is one. Although there are French natural numbers, the set of which also includes zero. But the main distinguishing features of both sets is the fact that they do not include either fractional or negative numbers.

The need to count a variety of objects arose in prehistoric times. Then the concept of “natural numbers” was supposedly formed. Its formation occurred throughout the entire process of changing a person’s worldview and the development of science and technology.

However, they could not yet think abstractly. It was difficult for them to understand what the commonality of the concepts of “three hunters” or “three trees” was. Therefore, when indicating the number of people, one definition was used, and when indicating the same number of objects of a different kind, a completely different definition was used.

And it was extremely short. It contained only the numbers 1 and 2, and the count ended with the concepts of “many”, “herd”, “crowd”, “heap”.

Later, a more progressive and broader account was formed. An interesting fact is that there were only two numbers - 1 and 2, and the next numbers were obtained by adding.

An example of this was the information that has reached us about the numerical series of the Australian tribe. They had 1 for the word “Enza”, and 2 for the word “petcheval”. The number 3 therefore sounded like “petcheval-Enza”, and 4 sounded like “petcheval-petcheval”.

Most peoples recognized fingers as the standard of counting. Further development of the abstract concept of “natural numbers” followed the path of using notches on a stick. And then it became necessary to designate a dozen with another sign. The ancient people found our way out - they began to use another stick, on which notches were made to indicate tens.

The ability to reproduce numbers expanded enormously with the advent of writing. At first, numbers were depicted as lines on clay tablets or papyrus, but gradually other writing icons began to be used. This is how Roman numerals appeared.

Much later, they appeared that opened up the possibility of writing numbers with a relatively small set of characters. Today it is not difficult to write down such huge numbers as the distance between planets and the number of stars. You just have to learn to use degrees.

Euclid in the 3rd century BC in the book “Elements” establishes the infinity of the numerical set, and Archimedes in “Psamita” reveals the principles for constructing the names of arbitrarily large numbers. Almost until the middle of the 19th century, people did not face the need for a clear formulation of the concept of “natural numbers”. The definition was required with the advent of the axiomatic mathematical method.

And in the 70s of the 19th century he formulated a clear definition of natural numbers, based on the concept of set. And today we already know that natural numbers are all integers, starting from 1 to infinity. Young children, taking their first step in becoming acquainted with the queen of all sciences - mathematics - begin to study these very numbers.

1.1.Definition

The numbers people use when counting are called natural(for example, one, two, three,..., one hundred, one hundred one,..., three thousand two hundred twenty-one,...) To write natural numbers, special signs (symbols) are used, called in numbers.

Nowadays it is accepted decimal number system. The decimal system (or method) of writing numbers uses Arabic numerals. These are ten different numeric characters: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 .

Least a natural number is a number one, it written using a decimal number - 1. The next natural number is obtained from the previous one (except for one) by adding 1 (one). This addition can be done many times (an infinite number of times). It means that No the greatest natural number. Therefore, they say that the series of natural numbers is unlimited or infinite, since it has no end. Natural numbers are written using decimal digits.

1.2. Number "zero"

To indicate the absence of something, use the number " zero" or " zero". It is written using numbers 0 (zero). For example, in a box all the balls are red. How many of them are green? - Answer: zero . This means there are no green balls in the box! The number 0 may mean that something has ended. For example, Masha had 3 apples. She shared two with friends and ate one herself. So she has left 0 (zero) apples, i.e. there is not a single one left. The number 0 may mean that something did not happen. For example, the hockey match Team Russia - Team Canada ended with the score 3:0 (we read “three - zero”) in favor of the Russian team. This means that the Russian team scored 3 goals, and the Canadian team scored 0 goals and could not score a single goal. We must remember that the number zero is not a natural number.

1.3. Writing natural numbers

In the decimal way of writing a natural number, each digit can represent a different number. It depends on the place of this digit in the number record. A certain place in the notation of a natural number is called position. Therefore, the decimal number system is called positional. Consider the decimal notation of 7777 seven thousand seven hundred seventy seven. This entry contains seven thousand, seven hundred, seven tens and seven units.

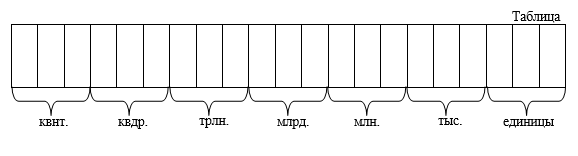
Each of the places (positions) in the decimal notation of a number is called discharge. Every three digits are combined into Class. This merging is done from right to left (from the end of the number record). Various categories and classes have their own names. The range of natural numbers is unlimited. Therefore, the number of ranks and classes is also not limited ( endlessly). Let's look at the names of digits and classes using the example of a number with decimal notation

38 001 102 987 000 128 425:

Classes and ranks
quintillions		hundreds of quintillions
		tens of quintillions
		quintillions
quadrillions		hundreds of quadrillions
		tens of quadrillions
		quadrillions
trillions		hundreds of trillions
		tens of trillions
		trillions
billions		hundreds of billions
		tens of billions
		billions
millions		hundreds of millions
		tens of millions
		millions
		hundreds of thousands
		tens of thousands

So, the classes, starting with the youngest, have names: units, thousands, millions, billions, trillions, quadrillions, quintillions.

1.4. Bit units

Each of the classes in the notation of natural numbers consists of three digits. Each rank has digit units. The following numbers are called digit units:

1 - digit unit of units digit,

10-digit unit of tens place,

100 - hundreds digit unit,

1 000 - thousand digit unit,

10 000 is a place unit of tens of thousands,

100,000 is a place unit for hundreds of thousands,

1,000,000 is the million digit unit, etc.

A number in any of the digits shows the number of units of this digit. Thus, the number 9, in the hundreds of billions place, means that the number 38,001,102,987,000 128,425 includes nine billion (i.e., 9 times 1,000,000,000 or 9 digit units of the billions place). An empty hundreds of quintillion place means that there are no hundreds of quintillion in the given number or their number is zero. In this case, the number 38 001 102 987 000 128 425 can be written as follows: 038 001 102 987 000 128 425.

You can write it differently: 000 038 001 102 987 000 128 425. Zeros at the beginning of the number indicate empty high-order digits. Usually they are not written, unlike zeros inside the decimal notation, which necessarily mark empty digits. Thus, three zeros in the millions class means that the hundreds of millions, tens of millions, and units of millions are empty.

1.5. Abbreviations for writing numbers

When writing natural numbers, abbreviations are used. Here are some examples:

1,000 = 1 thousand (one thousand)

23,000,000 = 23 million (twenty-three million)

5,000,000,000 = 5 billion (five billion)

203,000,000,000,000 = 203 trillion. (two hundred three trillion)

107,000,000,000,000,000 = 107 square meters. (one hundred seven quadrillion)

1,000,000,000,000,000,000 = 1 kwt. (one quintillion)

Block 1.1. Dictionary

Compile a dictionary of new terms and definitions from §1. To do this, write words from the list of terms below in the empty cells. In the table (at the end of the block), indicate for each definition the number of the term from the list.

Block 1.2. Self-preparation

In the world of big numbers

Economy .

Russia's budget for next year will be: 6328251684128 rubles.
The planned expenses for this year are: 5124983252134 rubles.
The country's income exceeded expenses by 1203268431094 rubles.

Questions and tasks

Read all three numbers given
Write the digits in the millions class for each of the three numbers.

To which section in each of the numbers does the digit located in the seventh position from the end of the number record belong?
What number of digit units is indicated by the number 2 in the entry of the first number?... in the entry of the second and third number?
Name the digit unit for the eighth position from the end in the notation of three numbers.

Geography (length)

Equatorial radius of the Earth: 6378245 m
Equator circumference: 40075696 m
The greatest depth of the world's oceans (Mariana Trench in the Pacific Ocean) 11500 m

Questions and tasks

Convert all three values to centimeters and read the resulting numbers.
For the first number (in cm), write down the numbers in the sections:

hundreds of thousands _______

tens of millions _______

thousands _______

billions _______

hundreds of millions _______

For the second number (in cm), write down the digit units corresponding to the numbers 4, 7, 5, 9 in the number notation

Convert the third value to millimeters and read the resulting number.
For all positions in the entry of the third number (in mm), indicate the digits and digit units in the table:

Geography (square)

The area of the entire surface of the Earth is 510,083 thousand square kilometers.
The surface area of sums on Earth is 148,628 thousand square kilometers.
The area of the Earth's water surface is 361,455 thousand square kilometers.

Questions and tasks

Convert all three values to square meters and read the resulting numbers.
Name the classes and categories corresponding to non-zero digits in the recording of these numbers (in sq. m).
In writing the third number (in sq. m), name the digit units corresponding to the numbers 1, 3, 4, 6.
In two entries of the second value (in sq. km. and sq. m), indicate which digits the number 2 belongs to.
Write the place value units for digit 2 in the second quantity notations.

Block 1.3. Dialogue with the computer.

It is known that large numbers are often used in astronomy. Let's give examples. The average distance of the Moon from the Earth is 384 thousand km. The distance of the Earth from the Sun (average) is 149,504 thousand km, the Earth from Mars is 55 million km. On a computer, using the Word text editor, create tables so that each digit in the entry of the indicated numbers is in a separate cell (cell). To do this, execute the commands on the toolbar: table → add table → number of rows (use the cursor to set “1”) → number of columns (calculate yourself). Create tables for other numbers (in the “Self-preparation” block).

Block 1.4. Big Numbers Relay

The first row of the table contains a large number. Read it. Then complete the tasks: by moving the numbers in the number record to the right or left, get the next numbers and read them. (Do not move the zeros at the end of the number!). In the classroom, the baton can be carried out by passing it to each other.

Line 2 . Move all the digits of the number in the first line to the left through two cells. Replace the numbers 5 with the next number. Fill empty cells with zeros. Read the number.

Line 3 . Move all the digits of the number in the second line to the right through three cells. Replace the numbers 3 and 4 in the number with the following numbers. Fill empty cells with zeros. Read the number.

Line 4. Move all digits of the number in line 3 one cell to the left. Replace the number 6 in the class of trillions with the previous one, and in the class of billions with the next number. Fill empty cells with zeros. Read the resulting number.

Line 5 . Move all digits of the number in line 4 one cell to the right. Replace the number 7 in the “tens of thousands” category with the previous one, and in the “tens of millions” category with the next one. Read the resulting number.

Line 6 . Move all the digits of the number in line 5 to the left through 3 cells. Replace the number 8 in the hundreds of billions place with the previous one, and the number 6 in the hundreds of millions place with the next number. Fill empty cells with zeros. Calculate the resulting number.

Line 7 . Move all digits of the number in line 6 to the right one cell. Swap the numbers in the tens of quadrillions and tens of billions places. Read the resulting number.

Line 8 . Move all the digits of the number in line 7 to the left through one cell. Swap the numbers in the quintillion and quadrillion places. Fill empty cells with zeros. Read the resulting number.

Line 9 . Move all the digits of the number in line 8 to the right through three cells. Swap two adjacent digits from the millions and trillions classes in a number line. Read the resulting number.

Line 10 . Move all digits of the number in line 9 one cell to the right. Read the resulting number. Select the numbers indicating the year of the Moscow Olympiad.

Block 1.5. let's play

Light the flame

The playing field is a drawing of a Christmas tree. It has 24 light bulbs. But only 12 of them are connected to the power grid. To select connected lamps, you must answer the questions correctly with “Yes” or “No”. The same game can be played on a computer; the correct answer “lights” the light bulb.

Is it true that numbers are special signs for writing natural numbers? (1 - yes, 2 - no)
Is it true that 0 is the smallest natural number? (3 - yes, 4 - no)
Is it true that in the positional number system the same digit can represent different numbers? (5 - yes, 6 - no)
Is it true that a certain place in the decimal notation of numbers is called a place? (7 - yes, 8 - no)
The number 543,384 is given. Is it true that the number of the highest digit units in it is 543, and the lowest digits are 384? (9 - yes, 10 - no)
Is it true that in the class of billions, the highest digit unit is one hundred billion, and the lowest is one billion? (11 - yes, 12 - no)
The number 458,121 is given. Is it true that the sum of the number of the highest digit units and the number of the lowest ones is 5? (13 - yes, 14 - no)
Is it true that the highest digit unit in the trillion class is a million times larger than the highest digit unit in the million class? (15 - yes, 16 - no)
Given two numbers 637,508 and 831. Is it true that the highest digit unit of the first number is 1000 times greater than the highest digit unit of the second number? (17 - yes, 18 - no)
Given the number 432. Is it true that the highest digit unit of this number is 2 times larger than the lowest? (19 - yes, 20 - no)
The number 100,000,000 is given. Is it true that the number of digit units in it that make up 10,000 is equal to 1000? (21 - yes, 22 - no)
Is it true that before the class of trillions there is a class of quadrillions, and before this class there is a class of quintillions? (23 - yes, 24 - no)

1.6. From the history of numbers

Since ancient times, people have been faced with the need to count the number of things, compare the quantities of objects (for example, five apples, seven arrows...; there are 20 men and thirty women in a tribe,...). There was also a need to establish order within a certain number of objects. For example, when hunting, the leader of the tribe goes first, the strongest warrior of the tribe comes second, etc. Numbers were used for these purposes. Special names were invented for them. In speech they are called numerals: one, two, three, etc. are cardinal numerals, and the first, second, third are ordinal numerals. Numbers were written using special characters - numbers.

Over time there appeared number systems. These are systems that include ways to write numbers and perform various operations on them. The most ancient known number systems are the Egyptian, Babylonian, and Roman number systems. In ancient times, in Rus', letters of the alphabet with a special sign ~ (title) were used to write numbers. Currently, the decimal number system is most widely used. Binary, octal and hexadecimal number systems are widely used, especially in the computer world.

So, to write the same number, you can use different signs - numbers. So, the number four hundred twenty-five can be written in Egyptian numerals - hieroglyphs:

This is the Egyptian way of writing numbers. This is the same number in Roman numerals: CDXXV(Roman way of writing numbers) or decimal digits 425 (decimal number system). In binary notation it looks like this: 110101001 (binary or binary number system), and in octal - 651 (octal number system). In the hexadecimal number system it will be written: 1A9(hexadecimal number system). You can do it quite simply: make, like Robinson Crusoe, four hundred and twenty-five notches (or strokes) on a wooden post - IIIIIIIII…... III. These are the very first images of natural numbers.

So, in the decimal system of writing numbers (in the decimal way of writing numbers) Arabic numerals are used. These are ten different symbols - numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 . In binary - two binary digits: 0, 1; in octal - eight octal digits: 0, 1, 2, 3, 4, 5, 6, 7; in hexadecimal - sixteen different hexadecimal digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F; in sexagesimal (Babylonian) - sixty different characters - numbers, etc.)

Decimal numbers came to European countries from the Middle East and Arab countries. Hence the name - Arabic numerals. But they came to the Arabs from India, where they were invented around the middle of the first millennium.

1.7. Roman number system

One of the ancient number systems that is used today is the Roman system. We present in the table the main numbers of the Roman number system and the corresponding numbers of the decimal system.

Roman numeral					C
				50 fifty		500 five hundred	1000 thousand

The Roman number system is addition system. In it, unlike positional systems (for example, decimal), each digit represents the same number. Yes, record II- denotes the number two (1 + 1 = 2), notation III- number three (1 + 1 + 1 = 3), notation XXX- the number thirty (10 + 10 + 10 = 30), etc. The following rules apply to writing numbers.

If the lower number is after larger, then it is added to the larger: VII- number seven (5 + 2 = 5 + 1 + 1 = 7), XVII- number seventeen (10 + 7 = 10 + 5 + 1 + 1 = 17), MCL- the number one thousand one hundred fifty (1000 + 100 + 50 = 1150).
If the lower number is before larger, then it is subtracted from the larger: IX- number nine (9 = 10 - 1), L.M.- number nine hundred and fifty (1000 - 50 = 950).

To write large numbers, you have to use (invent) new symbols - numbers. At the same time, recording numbers turns out to be cumbersome, and it is very difficult to perform calculations with Roman numerals. Thus, the year of launch of the first artificial Earth satellite (1957) in Roman records has the form MCMLVII .

Block 1. 8. Punched card

Reading natural numbers

These tasks are checked using a map with circles. Let us explain its application. Having completed all the tasks and found the correct answers (they are indicated by the letters A, B, C, etc.), place a sheet of transparent paper on the map. Use “X” signs to mark the correct answers on it, as well as the matching mark “+”. Then lay the clear sheet over the page so that the registration marks line up. If all the “X” marks are in the gray circles on this page, then the tasks were completed correctly.

1.9. Order of reading natural numbers

When reading a natural number, proceed as follows.

Mentally divide the number into triplets (classes) from right to left, from the end of the number.

Starting from the junior class, from right to left (from the end of the number) write down the names of classes: units, thousands, millions, billions, trillions, quadrillions, quintillions.
They read the number starting in high school. In this case, the number of bit units and the name of the class are called.
If the bit contains a zero (the bit is empty), then it is not called. If all three digits of the named class are zeros (the digits are empty), then this class is not called.

Let's read (name) the number written in the table (see §1), according to steps 1 - 4. Mentally divide the number 38001102987000128425 into classes from right to left: 038 001 102 987 000 128 425. We indicate the names of the classes in this number, starting from the end his records: units, thousands, millions, billions, trillions, quadrillions, quintillions. Now you can read the number, starting with the senior class. We name three-digit, two-digit and single-digit numbers, adding the name of the corresponding class. We do not name empty classes. We get the following number:

038 - thirty-eight quintillion
001 - one quadrillion
102 - one hundred two trillion
987 - nine hundred eighty seven billion
000 - we don’t name (don’t read)
128 - one hundred twenty eight thousand
425 - four hundred twenty five

As a result, we read the natural number 38 001 102 987 000 128 425 as follows: "thirty-eight quintillion one quadrillion one hundred two trillion nine hundred eighty-seven billion one hundred twenty-eight thousand four hundred twenty-five."

1.9. The order of writing natural numbers

Natural numbers are written in the following order.

Write down three digits of each class, starting with the highest class to the ones place. In this case, for the senior class there can be two or one digits.
If the class or category is not named, then zeros are written in the corresponding categories.

For example, number twenty five million three hundred two written in the form: 25 000 302 (the class of thousands is not named, so all digits of the class of thousands are written with zeros).

1.10. Representation of natural numbers as a sum of digit terms

Let's give an example: 7,563,429 is the decimal notation of a number seven million five hundred sixty three thousand four hundred twenty nine. This number contains seven million, five hundred thousand, six ten thousand, three thousand, four hundred, two tens and nine ones. It can be represented as the sum: 7,563,429 = 7,000,000 + 500,000 + 60,000 + + 3,000 + 400 + 20 + 9. This notation is called representing a natural number as a sum of digit terms.

Block 1.11. let's play

Dungeon Treasures

On the playing field is a drawing from Kipling's fairy tale "Mowgli". Five chests have padlocks. To open them, you need to solve problems. At the same time, by opening a wooden chest, you get one point. Opening a tin chest gives you two points, a copper chest gets three points, a silver chest gets four points, and a gold chest gets five points. The one who opens all the chests the fastest wins. The same game can be played on a computer.

Wooden chest

Find how much money (in thousand rubles) is in this chest. To do this, you need to find the total number of the lowest digit units of the million class for the number: 125308453231.

Tin chest

Find how much money (in thousand rubles) is in this chest. To do this, in the number 12530845323, find the number of the lowest digit units of the class of units and the number of the lowest digit units of the class of millions. Then find the sum of these numbers and add the number in the tens of millions place to the right.

Copper chest

To find the money in this chest (in thousands of rubles), you need to find in the number 751305432198203 the number of the lowest digit units in the class of trillions and the number of the lowest units in the class of billions. Then find the sum of these numbers and on the right write the natural numbers of the class of units of this number in the order of their location.

Silver chest

The money in this chest (in millions of rubles) will be shown by the sum of two numbers: the number of the lowest digit units of the class of thousands and the middle digit units of the class of billions for the number 481534185491502.

Golden chest

The number 800123456789123456789 is given. If we multiply the numbers in the highest digits of all classes of this number, we get the money of this chest in a million rubles.

Block 1.12. Match

Writing natural numbers. Representation of natural numbers as a sum of digit terms

For each task in the left column, select a solution from the right column. Write the answer in the form: 1a; 2g; 3b…


	Write the number in numbers: five million twenty five thousand
	Write the number in numbers: five billion twenty five million
	Write the number in numbers: five trillion twenty five
	Write the number in numbers: seventy-seven million seventy-seven thousand seven hundred seventy-seven
	Write the number in numbers: seventy-seven trillion seven hundred seventy-seven thousand seven
	Write the number in numbers: seventy-seven million seven hundred seventy-seven thousand seven
	Write the number in numbers: one hundred twenty-three billion four hundred fifty-six million seven hundred eighty-nine thousand
	Write the number in numbers: one hundred twenty-three million four hundred fifty-six thousand seven hundred eighty-nine
	Write the number in numbers: three billion eleven
	Write the number in numbers: three billion eleven million

Option 2


	thirty-two billion one hundred seventy-five million two hundred ninety-eight thousand three hundred forty-one		100000000 + 1000000 + 10000 + 100 + 1
	Present the number as a sum of digit terms: three hundred twenty-one million forty-one		30000000000 + 2000000000 + 100000000 + 70000000 + 5000000 + 200000 + 90000 + 8000 + 300 + 40 + 1
	Present the number as a sum of digit terms: 321000175298341
	Present the number as a sum of digit terms: 101010101
	Present the number as a sum of digit terms: 11111		300000000 + 20000000 + 1000000 +
	5000000 + 300000 + 20000 + 1000
	Write in decimal notation the number presented as a sum of digit terms: 5000000 + 300 + 20 + 1		30000000000000 + 2000000000000 + 1000000000000 + 100000000 + 70000000 + 5000000 + 200000 + 90000 + 8000 + 300 + 40 + 1
	Write in decimal notation the number presented as a sum of digit terms: 10000000000 + 2000000000 + 100000 + 10 + 9
	Write in decimal notation the number presented as a sum of digit terms: 10000000000 + 2000000000 + 100000000 + 10000000 + 9000000
	Write in decimal notation the number presented as a sum of digit terms: 9000000000000 + 9000000000 + 9000000 + 9000 + 9		10000 + 1000 + 100 + 10 + 1

Block 1.13. Facet test

The name of the test comes from the word “insect compound eye.” This is a complex eye consisting of individual “ocelli”. Facet test tasks are formed from individual elements indicated by numbers. Typically, facet tests contain a large number of tasks. But in this test there are only four tasks, but they are made up of a large number of elements. This is designed to teach you how to “assemble” test problems. If you can create them, you can easily cope with other facet tests.

Let us explain how tasks are composed using the example of the third task. It is composed of test elements numbered: 1, 4, 7, 11, 1, 5, 7, 9, 10, 16, 17, 22, 21, 25

« If» 1) take numbers (digit) from the table; 4) 7; 7) place it in a category; 11) billions; 1) take a number from the table; 5) 8; 7) place it in categories; 9) tens of millions; 10) hundreds of millions; 16) hundreds of thousands; 17) tens of thousands; 22) Place the numbers 9 and 6 in the thousands and hundreds places. 21) fill the remaining bits with zeros; " THAT» 26) we obtain a number equal to the time (period) of revolution of the planet Pluto around the Sun in seconds (s); " This number is equal to": 7880889600 p. In the answers it is indicated by the letter "V".

When solving problems, use a pencil to write the numbers in the cells of the table.

Facet test. Make up a number

The table contains the numbers:

1) take the number(s) from the table:

2) 4; 3) 5; 4) 7; 5) 8; 6) 9;

7) place this digit(s) in the digit(s);

8) hundreds of quadrillions and tens of quadrillions;

9) tens of millions;

10) hundreds of millions;

11) billions;

12) quintillions;

13) tens of quintillions;

14) hundreds of quintillions;

15) trillion;

16) hundreds of thousands;

17) tens of thousands;

18) fill the class(es) with it (them);

19) quintillions;

20) billion;

21) fill the remaining bits with zeros;

22) place the numbers 9 and 6 in the thousands and hundreds places;

23) we obtain a number equal to the mass of the Earth in tens of tons;

24) we get a number approximately equal to the volume of the Earth in cubic meters;

25) we get a number equal to the distance (in meters) from the Sun to the farthest planet of the solar system, Pluto;

26) we obtain a number equal to the time (period) of revolution of the planet Pluto around the Sun in seconds (s);

This number is equal to:

a) 5929000000000

b) 9999900000000000000000

d) 5980000000000000000000

Solve problems:

1, 3, 6, 5, 18, 19, 21, 23

1, 6, 7, 14, 13, 12, 8, 21, 24

1, 4, 7, 11, 1, 5, 7, 10, 9, 16, 17, 22, 21, 26

1, 3, 7, 15, 1, 6, 2, 6, 18, 20, 21, 25

Answers

1, 3, 6, 5, 18, 19, 21, 23 - g

1, 6, 7, 14, 13, 12, 8, 21, 24 - b

1, 4, 7, 11, 1, 5, 7, 10, 9, 16, 17, 22, 21, 26 - in

1, 3, 7, 15, 1, 6, 2, 6, 18, 20, 21, 25 - a

In mathematics, there are several different sets of numbers: real, complex, integer, rational, irrational, ... In our Everyday life We most often use natural numbers, since we encounter them when counting and when searching, designating the number of objects.

In contact with

What numbers are called natural numbers?

From ten digits you can write absolutely any existing sum of classes and ranks. Natural values are considered to be those which are used:

When counting any objects (first, second, third, ... fifth, ... tenth).
When indicating the number of items (one, two, three...)

N values are always integer and positive. There is no largest N because the set of integer values is unlimited.

Attention! Natural numbers are obtained when counting objects or when indicating their quantity.

Absolutely any number can be decomposed and presented in the form of digit terms, for example: 8.346.809=8 million+346 thousand+809 units.

Set N

The set N is in the set real, integer and positive. On the diagram of sets, they would be located in each other, since the set of natural ones is part of them.

The set of natural numbers is denoted by the letter N. This set has a beginning, but no end.

There is also an extended set N, where zero is included.

Smallest natural number

In most math schools, the smallest value of N is considered a unit, since the absence of objects is considered emptiness.

But in foreign mathematical schools, for example in French, it is considered natural. The presence of zero in the series makes the proof easier some theorems.

A series of values N that includes zero is called extended and is denoted by the symbol N0 (zero index).

Series of natural numbers

N series is a sequence of all N sets of digits. This sequence has no end.

The peculiarity of the natural series is that the next number will differ by one from the previous one, that is, it will increase. But the meanings cannot be negative.

Attention! For ease of counting, there are classes and categories:

Units (1, 2, 3),
Tens (10, 20, 30),
Hundreds (100, 200, 300),
Thousands (1000, 2000, 3000),
Tens of thousands (30,000),
Hundreds of thousands (800.000),
Millions (4000000), etc.

All N

All N are in the set of real, integer, non-negative values. They are theirs integral part.

These values go to infinity, they can belong to the classes of millions, billions, quintillions, etc.

For example:

Five apples, three kittens,
Ten rubles, thirty pencils,
One hundred kilograms, three hundred books,
A million stars, three million people, etc.

Sequence in N

In different mathematical schools you can find two intervals to which the sequence N belongs:

from zero to plus infinity, including ends, and from one to plus infinity, including ends, that is, everything positive integer answers.

N sets of digits can be either even or odd. Let's consider the concept of oddity.

Odd (any odd number ends in the numbers 1, 3, 5, 7, 9.) with two have a remainder. For example, 7:2=3.5, 11:2=5.5, 23:2=11.5.

What does even N mean?

Any even sums of classes end in numbers: 0, 2, 4, 6, 8. When even N is divided by 2, there will be no remainder, that is, the result is the whole answer. For example, 50:2=25, 100:2=50, 3456:2=1728.

Important! A number series of N cannot consist only of even or odd values, since they must alternate: even is always followed by odd, followed by even again, etc.

Properties N

Like all other sets, N has its own special properties. Let's consider the properties of the N series (not extended).

The value that is the smallest and that does not follow any other is one.
N represent a sequence, that is, one natural value follows another(except for one - it is the first).
When we perform computational operations on N sums of digits and classes (add, multiply), then the answer it always turns out natural meaning.
Permutation and combination can be used in calculations.
Each subsequent value cannot be less than the previous one. Also in the N series the following law will apply: if the number A is less than B, then in the number series there will always be a C for which the equality holds: A+C=B.
If we take two natural expressions, for example A and B, then one of the expressions will be true for them: A = B, A is greater than B, A is less than B.
If A is less than B, and B is less than C, then it follows that that A is less than C.
If A is less than B, then it follows that: if we add the same expression (C) to them, then A + C is less than B + C. It is also true that if these values are multiplied by C, then AC is less than AB.
If B is greater than A, but less than C, then it is true: B-A is less than C-A.

Attention! All of the above inequalities are also valid in the opposite direction.

What are the components of multiplication called?

In many simple and even complex problems, finding the answer depends on the skills of schoolchildren.

In order to multiply quickly and correctly and be able to solve inverse problems, you need to know the components of multiplication.

15. 10=150. In this expression there are 15 and 10 are multipliers, and 150 is a product.

Multiplication has properties that are necessary when solving problems, equations and inequalities:

Rearranging the factors will not change the final product.
To find an unknown factor, you need to divide the product by a known factor (true for all factors).

For example: 15 . X=150. Let's divide the product by a known factor. 150:15=10. Let's do a check. 15 . 10=150. According to this principle, they even decide complex linear equations(to simplify them).

Important! A product can consist of more than just two factors. For example: 840=2 . 5. 7. 3. 4

What are natural numbers in mathematics?

Places and classes of natural numbers

Conclusion

Let's summarize. N is used when counting or indicating the number of items. The series of natural sets of numbers is infinite, but it includes only integer and positive sums of digits and classes. Multiplication is also necessary in order to to count objects, as well as for solving problems, equations and various inequalities.

Mathematics emerged from general philosophy around the sixth century BC. e., and from that moment her victorious march around the world began. Each stage of development introduced something new - elementary counting evolved, transformed into differential and integral calculus, centuries passed, formulas became more and more confusing, and the moment came when “the most complex mathematics began - all numbers disappeared from it.” But what was the basis?

The beginning of time

Natural numbers appeared along with the first mathematical operations. One spine, two spines, three spines... They appeared thanks to Indian scientists who developed the first positional

The word “positionality” means that the location of each digit in a number is strictly defined and corresponds to its rank. For example, the numbers 784 and 487 are the same numbers, but the numbers are not equivalent, since the first includes 7 hundreds, while the second only 4. The Indian innovation was picked up by the Arabs, who brought the numbers to the form that we know Now.

In ancient times, numbers were given a mystical meaning; Pythagoras believed that number underlies the creation of the world along with the basic elements - fire, water, earth, air. If we consider everything only from the mathematical side, then what is a natural number? The field of natural numbers is denoted as N and is an infinite series of numbers that are integers and positive: 1, 2, 3, … + ∞. Zero is excluded. Used primarily to count items and indicate order.

What is it in mathematics? Peano's axioms

Field N is the basic one on which elementary mathematics is based. Over time, fields of integer, rational,

The work of the Italian mathematician Giuseppe Peano made possible the further structuring of arithmetic, achieved its formality and prepared the way for further conclusions that went beyond the field area N.

What a natural number is was clarified earlier in simple language; below we will consider the mathematical definition based on the Peano axioms.

One is considered a natural number.
The number that follows a natural number is a natural number.
There is no natural number before one.
If the number b follows both the number c and the number d, then c=d.
An axiom of induction, which in turn shows what a natural number is: if some statement that depends on a parameter is true for the number 1, then we assume that it also works for the number n from the field of natural numbers N. Then the statement is also true for n =1 from the field of natural numbers N.

Basic operations for the field of natural numbers

Since field N was the first for mathematical calculations, both the domains of definition and the ranges of values of a number of operations below belong to it. They are closed and not. The main difference is that closed operations are guaranteed to leave the result within the set N, regardless of what numbers are involved. It is enough that they are natural. The outcome of other numerical interactions is no longer so clear and directly depends on what kind of numbers are involved in the expression, since it may contradict the main definition. So, closed operations:

addition - x + y = z, where x, y, z are included in the N field;
multiplication - x * y = z, where x, y, z are included in the N field;
exponentiation - x y, where x, y are included in the N field.

The remaining operations, the result of which may not exist in the context of the definition of “what is a natural number,” are as follows:

Properties of numbers belonging to the field N

All further mathematical reasoning will be based on the following properties, the most trivial, but no less important.

The commutative property of addition is x + y = y + x, where the numbers x, y are included in the field N. Or the well-known “the sum does not change by changing the places of the terms.”
The commutative property of multiplication is x * y = y * x, where the numbers x, y are included in the N field.
The combinational property of addition is (x + y) + z = x + (y + z), where x, y, z are included in the N field.
The matching property of multiplication is (x * y) * z = x * (y * z), where the numbers x, y, z are included in the N field.
distributive property - x (y + z) = x * y + x * z, where the numbers x, y, z are included in the N field.

Pythagorean table

One of the first steps in students’ knowledge of the entire structure of elementary mathematics after they have understood for themselves which numbers are called natural numbers is the Pythagorean table. It can be considered not only from the point of view of science, but also as a most valuable scientific monument.

This multiplication table has undergone a number of changes over time: zero has been removed from it, and numbers from 1 to 10 represent themselves, without taking into account orders (hundreds, thousands...). It is a table in which the row and column headings are numbers, and the contents of the cells where they intersect are equal to their product.

In the practice of teaching in recent decades, there has been a need to memorize the Pythagorean table “in order,” that is, memorization came first. Multiplication by 1 was excluded because the result was a multiplier of 1 or greater. Meanwhile, in the table with the naked eye you can notice a pattern: the product of numbers increases by one step, which is equal to the title of the line. Thus, the second factor shows us how many times we need to take the first one in order to obtain the desired product. This system is much more convenient than the one that was practiced in the Middle Ages: even understanding what a natural number is and how trivial it is, people managed to complicate their everyday counting by using a system that was based on powers of two.

Subset as the cradle of mathematics

At the moment, the field of natural numbers N is considered only as one of the subsets of complex numbers, but this does not make them any less valuable in science. Natural number is the first thing a child learns when studying himself and the world around him. One finger, two fingers... Thanks to it, a person develops logical thinking, as well as the ability to determine the cause and deduce the effect, paving the way for great discoveries.

Natural numbers are one of the oldest mathematical concepts.

In the distant past, people did not know numbers, and when they needed to count objects (animals, fish, etc.), they did it differently than we do now.

The number of objects was compared with parts of the body, for example, with fingers on a hand, and they said: “I have as many nuts as there are fingers on my hand.”

Over time, people realized that five nuts, five goats and five hares have a common property - their number is equal to five.

Remember!

Integers- these are numbers, starting from 1, obtained by counting objects.

1, 2, 3, 4, 5…

Smallest natural number — 1 .

Largest natural number does not exist.

When counting, the number zero is not used. Therefore, zero is not considered a natural number.

People learned to write numbers much later than to count. First of all, they began to depict one with one stick, then with two sticks - the number 2, with three - the number 3.

| — 1, || — 2, ||| — 3, ||||| — 5 …

Then special signs appeared to designate numbers - the predecessors of modern numbers. The numerals we use to write numbers originated in India approximately 1,500 years ago. The Arabs brought them to Europe, which is why they are called Arabic numerals.

There are ten numbers in total: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Using these numbers you can write any natural number.

Remember!

Natural series is the sequence of all natural numbers:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …

In the natural series, each number is greater than the previous one by 1.

The natural series is infinite; there is no greatest natural number in it.

The counting system we use is called decimal positional.

Decimal because 10 units of each digit form 1 unit of the most significant digit. Positional because the meaning of a digit depends on its place in the number record, that is, on the digit in which it is written.

Important!

The classes following the billion are named according to the Latin names of numbers. Each subsequent unit contains a thousand previous ones.

1,000 billion = 1,000,000,000,000 = 1 trillion (“three” is Latin for “three”)
1,000 trillion = 1,000,000,000,000,000 = 1 quadrillion (“quadra” is Latin for “four”)
1,000 quadrillion = 1,000,000,000,000,000,000 = 1 quintillion (“quinta” is Latin for “five”)

However, physicists have found a number that exceeds the number of all atoms (the smallest particles of matter) in the entire Universe.

This number received a special name - googol. Googol is a number with 100 zeros.