Let's construct a confidence interval in MS EXCEL to estimate the mean value of the distribution in the case of a known dispersion value.

Of course the choice level of trust completely depends on the problem being solved. Thus, the degree of confidence of an air passenger in the reliability of an airplane should undoubtedly be higher than the degree of confidence of a buyer in the reliability of an electric light bulb.

Problem formulation

Let us assume that from population having been taken sample size n. It is assumed that standard deviation this distribution is known. It is necessary based on this samples evaluate the unknown distribution mean(μ, ) and construct the corresponding double-sided confidence interval.

Point estimate

As is known from statistics(let's denote it X avg) is unbiased estimate of the mean this population and has a distribution N(μ;σ 2 /n).

Note: What to do if you need to build confidence interval in the case of a distribution that is not normal? In this case, comes to the rescue, which states that with a sufficiently large size samples n from distribution not being normal, sample distribution of statistics X avg will approximately correspond normal distribution with parameters N(μ;σ 2 /n).

So, point estimate average distribution values we have - this sample mean, i.e. X avg. Now let's get started confidence interval.

Constructing a confidence interval

Usually, knowing the distribution and its parameters, we can calculate the probability that the random variable will take a value from the interval we specify. Now let’s do the opposite: find the interval in which the random variable will fall with a given probability. For example, from the properties normal distribution it is known that with a probability of 95%, a random variable distributed over normal law, will fall within the range of approximately +/- 2 from average value(see article about). This interval will serve as a prototype for us confidence interval.

Now let's see if we know the distribution , to calculate this interval? To answer the question, we must indicate the shape of the distribution and its parameters.

We know the form of distribution - this is normal distribution(remember that we are talking about sampling distribution statistics X avg).

The parameter μ is unknown to us (it just needs to be estimated using confidence interval), but we have an estimate of it X avg, calculated based on samples, which can be used.

Second parameter - standard deviation of sample mean we will consider it known, it is equal to σ/√n.

Because we don’t know μ, then we will build the interval +/- 2 standard deviations not from average value, and from its known estimate X avg. Those. when calculating confidence interval we will NOT assume that X avg falls within the range +/- 2 standard deviations from μ with a probability of 95%, and we will assume that the interval is +/- 2 standard deviations from X avg with 95% probability it will cover μ – average of the general population, from which it is taken sample. These two statements are equivalent, but the second statement allows us to construct confidence interval.

In addition, let us clarify the interval: a random variable distributed over normal law, with a 95% probability falls within the interval +/- 1.960 standard deviations, not +/- 2 standard deviations. This can be calculated using the formula =NORM.ST.REV((1+0.95)/2), cm. example file Sheet Interval.

Now we can formulate a probabilistic statement that will serve us to form confidence interval:
"The probability that population mean located from sample average within 1,960 " standard deviations of the sample mean", equal to 95%".

The probability value mentioned in the statement has a special name , which is associated with significance level α (alpha) by a simple expression trust level =1 -α . In our case significance level α =1-0,95=0,05 .

Now, based on this probabilistic statement, we write an expression for calculating confidence interval:

where Z α/2 – standard normal distribution(this value of the random variable z, What P(z>=Z α/2 )=α/2).

Note: Upper α/2-quantile defines the width confidence interval V standard deviations sample mean. Upper α/2-quantile standard normal distribution always greater than 0, which is very convenient.

In our case, with α=0.05, upper α/2-quantile equals 1.960. For other significance levels α (10%; 1%) upper α/2-quantile Z α/2 can be calculated using the formula =NORM.ST.REV(1-α/2) or, if known trust level, =NORM.ST.OBR((1+trust level)/2).

Usually when building confidence intervals for estimating the mean use only upper α/2-quantile and don't use lower α/2-quantile. This is possible because standard normal distribution symmetrically about the x axis ( its distribution density symmetrical about average, i.e. 0). Therefore, there is no need to calculate lower α/2-quantile(it is simply called α /2-quantile), because it is equal upper α/2-quantile with a minus sign.

Let us recall that, despite the shape of the distribution of the value x, the corresponding random variable X avg distributed approximately Fine N(μ;σ 2 /n) (see article about). Therefore, in general, the above expression for confidence interval is only an approximation. If the value x is distributed over normal law N(μ;σ 2 /n), then the expression for confidence interval is accurate.

Confidence interval calculation in MS EXCEL

Let's solve the problem.
The response time of an electronic component to an input signal is an important characteristic of the device. An engineer wants to construct a confidence interval for the average response time at a confidence level of 95%. From previous experience, the engineer knows that the standard deviation of response time is 8 ms. It is known that to evaluate the response time, the engineer made 25 measurements, the average value was 78 ms.

Solution: An engineer wants to know the response time of an electronic device, but he understands that the response time is not a fixed value, but a random variable that has its own distribution. So, the best he can hope for is to determine the parameters and shape of this distribution.

Unfortunately, from the problem conditions we do not know the shape of the response time distribution (it does not have to be normal). , this distribution is also unknown. Only him is known standard deviationσ=8. Therefore, while we cannot calculate the probabilities and construct confidence interval.

However, despite the fact that we do not know the distribution time separate response, we know that according to CPT, sampling distribution average response time is approximately normal(we will assume that the conditions CPT are carried out, because size samples quite large (n=25)) .

Moreover, average this distribution is equal to average value distribution of a single response, i.e. μ. A standard deviation of this distribution (σ/√n) can be calculated using the formula =8/ROOT(25) .

It is also known that the engineer received point estimate parameter μ equal to 78 ms (X avg). Therefore, now we can calculate probabilities, because we know the form of distribution ( normal) and its parameters (X avg and σ/√n).

Engineer wants to know expected valueμ response time distributions. As stated above, this μ is equal to mathematical expectation of the sample distribution of the average response time. If we use normal distribution N(X avg; σ/√n), then the desired μ will be in the range +/-2*σ/√n with a probability of approximately 95%.

Significance level equals 1-0.95=0.05.

Finally, let's find the left and right border confidence interval.
Left border: =78-NORM.ST.REV(1-0.05/2)*8/ROOT(25) = 74,864
Right border: =78+NORM.ST.INV(1-0.05/2)*8/ROOT(25)=81.136

Left border: =NORM.REV(0.05/2; 78; 8/ROOT(25))
Right border: =NORM.REV(1-0.05/2; 78; 8/ROOT(25))

Answer: confidence interval at 95% confidence level and σ=8msec equals 78+/-3.136 ms.

IN example file on the Sigma sheet known, created a form for calculation and construction double-sided confidence interval for arbitrary samples with given σ and level of significance.

CONFIDENCE.NORM() function

If the values samples are in the range B20:B79 , A significance level equal to 0.05; then the MS EXCEL formula:
=AVERAGE(B20:B79)-CONFIDENCE.NORM(0.05;σ; COUNT(B20:B79))
will return the left border confidence interval.

The same limit can be calculated using the formula:
=AVERAGE(B20:B79)-NORM.ST.REV(1-0.05/2)*σ/ROOT(COUNT(B20:B79))

Note: The CONFIDENCE.NORM() function appeared in MS EXCEL 2010. In earlier versions of MS EXCEL, the TRUST() function was used.

Confidence interval for mathematical expectation - this is an interval calculated from data that, with a known probability, contains the mathematical expectation of the general population. A natural estimate for the mathematical expectation is the arithmetic mean of its observed values. Therefore, throughout the lesson we will use the terms “average” and “average value”. In problems of calculating a confidence interval, an answer most often required is something like “The confidence interval of the average number [value in a particular problem] is from [smaller value] to [larger value].” Using a confidence interval, you can evaluate not only average values, but also the proportion of a particular characteristic of the general population. Average values, dispersion, standard deviation and error, through which we will arrive at new definitions and formulas, are discussed in the lesson Characteristics of the sample and population .

Point and interval estimates of the mean

If the average value of the population is estimated by a number (point), then a specific average, which is calculated from a sample of observations, is taken as an estimate of the unknown average value of the population. In this case, the value of the sample mean - a random variable - does not coincide with the mean value of the general population. Therefore, when indicating the sample mean, you must simultaneously indicate the sampling error. The measure of sampling error is the standard error, which is expressed in the same units as the mean. Therefore, the following notation is often used: .

If the estimate of the average needs to be associated with a certain probability, then the parameter of interest in the population must be assessed not by one number, but by an interval. A confidence interval is an interval in which, with a certain probability P the value of the estimated population indicator is found. Confidence interval in which it is probable P = 1 - α the random variable is found, calculated as follows:

,

α = 1 - P, which can be found in the appendix to almost any book on statistics.

In practice, the population mean and variance are not known, so the population variance is replaced by the sample variance, and the population mean by the sample mean. Thus, the confidence interval in most cases is calculated as follows:

.

The confidence interval formula can be used to estimate the population mean if

• the standard deviation of the population is known;
• or the standard deviation of the population is unknown, but the sample size is greater than 30.

The sample mean is an unbiased estimate of the population mean. In turn, the sample variance is not an unbiased estimate of the population variance. To obtain an unbiased estimate of the population variance in the sample variance formula, sample size n should be replaced by n-1.

Example 1. Information was collected from 100 randomly selected cafes in a certain city that the average number of employees in them is 10.5 with a standard deviation of 4.6. Determine the 95% confidence interval for the number of cafe employees.

where is the critical value of the standard normal distribution for the significance level α = 0,05 .

Thus, the 95% confidence interval for the average number of cafe employees ranged from 9.6 to 11.4.

Example 2. For a random sample from a population of 64 observations, the following total values ​​were calculated:

sum of values ​​in observations,

sum of squared deviations of values ​​from the mean .

Calculate the 95% confidence interval for the mathematical expectation.

Let's calculate the standard deviation:

,

Let's calculate the average value:

.

We substitute the values ​​into the expression for the confidence interval:

where is the critical value of the standard normal distribution for the significance level α = 0,05 .

We get:

Thus, the 95% confidence interval for the mathematical expectation of this sample ranged from 7.484 to 11.266.

Example 3. For a random population sample of 100 observations, the calculated mean is 15.2 and standard deviation is 3.2. Calculate the 95% confidence interval for the expected value, then the 99% confidence interval. If the sample power and its variation remain unchanged and the confidence coefficient increases, will the confidence interval narrow or widen?

We substitute these values ​​into the expression for the confidence interval:

where is the critical value of the standard normal distribution for the significance level α = 0,05 .

We get:

.

Thus, the 95% confidence interval for the mean of this sample ranged from 14.57 to 15.82.

We again substitute these values ​​into the expression for the confidence interval:

where is the critical value of the standard normal distribution for the significance level α = 0,01 .

We get:

.

Thus, the 99% confidence interval for the mean of this sample ranged from 14.37 to 16.02.

As we see, as the confidence coefficient increases, the critical value of the standard normal distribution also increases, and, consequently, the starting and ending points of the interval are located further from the mean, and thus the confidence interval for the mathematical expectation increases.

Point and interval estimates of specific gravity

The share of some sample attribute can be interpreted as a point estimate of the share p of the same characteristic in the general population. If this value needs to be associated with probability, then the confidence interval of the specific gravity should be calculated p characteristic in the population with probability P = 1 - α :

.

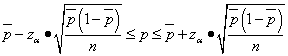Example 4. In some city there are two candidates A And B are running for mayor. 200 city residents were randomly surveyed, of which 46% responded that they would vote for the candidate A, 26% - for the candidate B and 28% do not know who they will vote for. Determine the 95% confidence interval for the proportion of city residents supporting the candidate A.

Purpose of the service. Using this service, you can determine:

• confidence interval for the general mean, confidence interval for the variance;
• confidence interval for the standard deviation, confidence interval for the general share;

Example No. 1. On a collective farm, out of a total herd of 1000 sheep, 100 sheep underwent selective control shearing. As a result, an average wool clipping of 4.2 kg per sheep was established. Determine with a probability of 0.99 the mean square error of the sample when determining the average wool shearing per sheep and the limits within which the shearing value is contained if the variance is 2.5. The sample is non-repetitive.
Example No. 2. From a batch of imported products at the post of the Moscow Northern Customs, 20 samples of product “A” were taken by random repeated sampling. As a result of the test, the average moisture content of product “A” in the sample was established, which turned out to be equal to 6% with a standard deviation of 1%.
Determine with probability 0.683 the limits of the average moisture content of the product in the entire batch of imported products.
Example No. 3. A survey of 36 students showed that the average number of textbooks read by them during the academic year was equal to 6. Assuming that the number of textbooks read by a student per semester has a normal distribution law with a standard deviation equal to 6, find: A) with a reliability of 0 .99 interval estimate for the mathematical expectation of this random variable; B) with what probability can we say that the average number of textbooks read by a student per semester, calculated from this sample, will deviate from the mathematical expectation in absolute value by no more than 2.

Classification of confidence intervals

By sample type:

1. Confidence interval for an infinite sample;
2. Confidence interval for the final sample;

Calculation of the average sampling error for random sampling

Average sampling error formulas
re-selection		repeat selection
for average	for share	for average	for share

Formulas for calculating the sample size using a purely random sampling method