Розкладання cos у ряд тейлору. Розкладання функцій у статечні ряди
16.1. Розкладання елементарних функцій у ряди Тейлора та
Маклорена
Покажемо, якщо довільна функція задана на безлічі  , на околиці точки
, на околиці точки  має безліч похідних і є сумою статечного ряду:
має безліч похідних і є сумою статечного ряду:
то можна визначити коефіцієнти цього ряду.
Підставимо в статечний ряд  . Тоді
. Тоді  .
.
Знайдемо першу похідну функції  :
:
При  :
: .
.
Для другої похідної отримаємо:
При  :
: .
.
Продовжуючи цю процедуру nраз отримаємо:  .
.
Таким чином, отримали статечний ряд виду:


 ,
,
який називається поряд Тейлорадля функції  в околиці точки
в околиці точки  .
.
Приватним випадком ряду Тейлора є ряд Маклоренапри  :
:



Залишок ряду Тейлора (Маклорена) виходить відкиданням від основних рядів nперших членів і позначається як  . Тоді функцію
. Тоді функцію  можна записати як суму nперших членів ряду
можна записати як суму nперших членів ряду  та залишку
та залишку  :,
:,
 .
.
Залишок зазвичай  виражають різними формулами.
виражають різними формулами.
Одна з них у формі Лагранжа:
 , де
, де  .
. .
.
Зауважимо, що на практиці частіше використовується ряд Маклорена. Таким чином, для того, щоб записати функцію  у вигляді суми ступеневого ряду необхідно:
у вигляді суми ступеневого ряду необхідно:
1) визначити коефіцієнти низки Маклорена (Тейлора);
2) знайти область збіжності отриманого статечногоряду;
3) довести, що даний ряд сходить до функції  .
.
Теорема1
(Необхідна та достатня умова збіжності ряду Маклорена). Нехай радіус збіжності ряду  . Для того щоб цей ряд сходився в інтервалі
. Для того щоб цей ряд сходився в інтервалі  до функції
до функції  ,необхідно і достатньо, щоб виконувалася умова:
,необхідно і достатньо, щоб виконувалася умова:  у вказаному інтервалі.
у вказаному інтервалі.
Теорема 2.Якщо похідні будь-якого порядку функції  у деякому проміжку
у деякому проміжку  обмежені за абсолютною величиною одним і тим самим числом M, тобто
обмежені за абсолютною величиною одним і тим самим числом M, тобто  , то в цьому проміжку функцію
, то в цьому проміжку функцію  можна розкласти в ряд Маклорена.
можна розкласти в ряд Маклорена.
приклад1
.
Розкласти в ряд Тейлора навколишнього місця  функцію.
функцію.
Рішення.
 .
.
 ,;
,;
 ,
, ;
;
 ,
, ;
;
 ,
,
.......................................................................................................................................
 ,
, ;
;
Область збіжності  .
.
приклад2
.
Розкласти функцію  в ряд Тейлора навколишнього місця
в ряд Тейлора навколишнього місця  .
.
Рішення:
Знаходимо значення функції та її похідних при  .
.
 ,
, ;
;
 ,
, ;
;
...........……………………………
 ,
, .
.
Підставляємо ці значення до ряду. Отримуємо:
або  .
.
Знайдемо область збіжності цього ряду. За ознакою Даламбера ряд сходиться, якщо
 .
.
Отже, за будь-якого  цей гранично менше 1, а тому область збіжності ряду буде:
цей гранично менше 1, а тому область збіжності ряду буде:  .
.
Розглянемо кілька прикладів розкладання в ряд Маклорена основних елементарних функцій. Нагадаємо, що ряд Маклорена:


 .
.
сходиться на інтервалі  до функції
до функції  .
.
Зазначимо, що для розкладання функції до ряду необхідно:
а) визначити коефіцієнти низки Маклорена цієї функції;
б) обчислити радіус збіжності для одержаного ряду;
в) довести, що отриманий ряд сходить до функції  .
.
приклад 3.Розглянемо функцію  .
.
Рішення.
Обчислимо значення функції та її похідних при  .
.
Тоді числові коефіцієнти ряду мають вигляд:
для будь-кого n.Підставимо знайдені коефіцієнти в ряд Маклорена та отримаємо: 
Знайдемо радіус збіжності отриманого ряду, а саме:
 .
.
Отже, ряд сходиться на інтервалі  .
.
Цей ряд сходить до функції  за будь-яких значень
за будь-яких значень  тому що на будь-якому проміжку
тому що на будь-якому проміжку  функція
функція  її похідні по абсолютній величині обмежені числом
її похідні по абсолютній величині обмежені числом  .
.
приклад4
.
Розглянемо функцію  .
.
Рішення.
 :
:

Неважко помітити, що похідні парного порядку  , а похідні непарного порядку. Підставимо знайдені коефіцієнти в ряд Маклорена і отримаємо розкладання:
, а похідні непарного порядку. Підставимо знайдені коефіцієнти в ряд Маклорена і отримаємо розкладання:
Знайдемо інтервал збіжності цього ряду. За ознакою Даламбер:
для будь-кого  . Отже, ряд сходиться на інтервалі
. Отже, ряд сходиться на інтервалі  .
.
Цей ряд сходить до функції  тому що всі її похідні обмежені одиницею.
тому що всі її похідні обмежені одиницею.
приклад5
.
 .
.
Рішення.
Знайдемо значення функції та її похідних при  :
:

Таким чином, коефіцієнти даного ряду:  і
і  , отже:
, отже:
Аналогічно з попереднім рядом область збіжності  . Ряд сходить до функції
. Ряд сходить до функції  тому що всі її похідні обмежені одиницею.
тому що всі її похідні обмежені одиницею.
Звернемо увагу, що функція  непарна і розкладання в ряд по непарних ступенях, функція
непарна і розкладання в ряд по непарних ступенях, функція  – парна та розкладання в ряд за парними ступенями.
– парна та розкладання в ряд за парними ступенями.
приклад6
.
Біноміальний ряд:  .
.
Рішення.
Знайдемо значення функції та її похідних при  :
:

Звідси видно, що:

Підставимо ці значення коефіцієнтів у ряд Маклорена і отримаємо розкладання даної функції в статечний ряд:
Знайдемо радіус збіжності цього ряду:

Отже, ряд сходиться на інтервалі  . У граничних точках при
. У граничних точках при  і
і  ряд може сходитися чи ні в залежності від показника ступеня
ряд може сходитися чи ні в залежності від показника ступеня  .
.
Досліджений ряд сходиться на інтервалі  до функції
до функції  , тобто сумаряду
, тобто сумаряду  при
при  .
.
приклад7
.
Розкладемо у ряд Маклорена функцію  .
.
Рішення.
Для розкладання ряду цієї функції використовуємо біноміальний ряд при  . Отримаємо:
. Отримаємо: 
На основі властивості статечних рядів (статечний ряд можна інтегрувати в області його збіжності) знайдемо інтеграл від лівої та правої частин даного ряду:
Знайдемо область збіжності цього ряду:  ,
,
тобто областю збіжності даного ряду є інтервал  . Визначимо збіжність низки кінцях інтервалу. При
. Визначимо збіжність низки кінцях інтервалу. При 
 . Цей ряд є гармонійним поряд, тобто розходиться. При
. Цей ряд є гармонійним поряд, тобто розходиться. При  отримаємо числовий ряд із загальним членом
отримаємо числовий ряд із загальним членом  .
.
Ряд за ознакою Лейбніца сходиться. Таким чином, областю збіжності даного ряду є проміжок  .
.
16.2. Застосування статечних рядів ступенів у наближених обчисленнях
У наближених обчисленнях статечні ряди грають винятково велику роль. З їх допомогою складено таблиці тригонометричних функцій, таблиці логарифмів, таблиці значень інших функцій, які використовують у різних галузях знань, наприклад, у теорії ймовірностей та математичної статистики. Крім того, розкладанняфункцій у статечний ряд корисно для їх теоретичного дослідження. Головним питанням при використанні статечних рядів у наближених обчисленнях є питання оцінки похибки при заміні суми ряду сумою його перших nчленів.
Розглянемо два випадки:
функція розкладена в ряд, що знак чергується;
функцію розкладено в знакопостійний ряд.
Обчислення за допомогою рядів, що чергуються.
Нехай функція  розкладена в знакочередний статечний ряд. Тоді при обчисленні цієї функції для конкретного значення
розкладена в знакочередний статечний ряд. Тоді при обчисленні цієї функції для конкретного значення  отримуємо числовий ряд, до якого можна застосувати ознаку Лейбніца. Відповідно до цієї ознаки, якщо суму ряду замінити сумою його перших nчленів, то абсолютна похибка не перевищує першого члена залишку цього ряду, тобто:
отримуємо числовий ряд, до якого можна застосувати ознаку Лейбніца. Відповідно до цієї ознаки, якщо суму ряду замінити сумою його перших nчленів, то абсолютна похибка не перевищує першого члена залишку цього ряду, тобто:  .
.
приклад8
.
Обчислити  із точністю до 0,0001.
із точністю до 0,0001.
Рішення.
Будемо використовувати ряд Маклорена для  , Підставивши значення кута в радіанах:
, Підставивши значення кута в радіанах:

Якщо порівняти перший і другий члени низки із заданою точністю, то: .
Третій член розкладання:
менше заданої точності обчислення. Отже, для обчислення  достатньо залишити два члени ряду, тобто
достатньо залишити два члени ряду, тобто
 .
.
Таким чином  .
.
приклад9
.
Обчислити  із точністю 0,001.
із точністю 0,001.
Рішення.
Використовуватимемо формулу біноміального ряду. Для цього запишемо  у вигляді:
у вигляді:  .
.
У цьому виразі  ,
,

Порівняємо кожен із членів ряду з точністю, яка задана. Видно що  . Отже, для обчислення
. Отже, для обчислення  достатньо залишити три члени ряду.
достатньо залишити три члени ряду.
 або
або  .
.
Обчислення за допомогою позитивних рядів
приклад10
.
Обчислити число  із точністю до 0,001.
із точністю до 0,001.
Рішення.
В ряд для функції  підставимо
підставимо  . Отримаємо:
. Отримаємо:

Оцінимо похибку, що виникає при заміні суми ряду сумою перших  членів. Запишемо очевидну нерівність:
членів. Запишемо очевидну нерівність:
тобто 2< <3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
<3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
 ,
, .
.
За умовою завдання потрібно знайти nтаке, щоб виконувалася нерівність:  або
або  .
.
Легко перевірити, що за n= 6: .
.
Отже,  .
.
приклад11
.
Обчислити  з точністю0,0001.
з точністю0,0001.
Рішення.
Зауважимо, що з обчислення логарифмів можна було б застосувати ряд для функції  Але цей ряд дуже повільно сходиться і для досягнення заданої точності потрібно було б взяти 9999 членів! Тому для обчислення логарифмів, як правило, використовується ряд для функції
Але цей ряд дуже повільно сходиться і для досягнення заданої точності потрібно було б взяти 9999 членів! Тому для обчислення логарифмів, як правило, використовується ряд для функції  , що сходиться на інтервалі
, що сходиться на інтервалі  .
.
Обчислимо  за допомогою цього ряду. Нехай
за допомогою цього ряду. Нехай  тоді
тоді  .
.
Отже,  ,
,
Для того, щоб обчислити  із заданою точністю, візьмемо суму перших чотирьох членів:
із заданою точністю, візьмемо суму перших чотирьох членів:  .
.
Залишок ряду  відкинемо. Оцінимо похибку. Очевидно, що
відкинемо. Оцінимо похибку. Очевидно, що 
або  .
.

Таким чином, у ряду, який був використаний для обчислення, достатньо було взяти тільки чотириперші складові замість 9999 у ряді для функції  .
.
Запитання для самодіагностики
1. Що таке ряд Тейлора?
2. Який вид мав ряд Маклорена?
3. Сформулювати теорему про розкладання функції до ряду Тейлора.
4. Записати розкладання до ряду Маклорена основних функцій.
5. Вказати області збіжності розглянутих рядів.
6. Як виконати оцінку похибки в наближених обчисленнях за допомогою статечних рядів?
Якщо функція f(x) має деякому інтервалі, що містить точку а, похідні всіх порядків, то до неї може бути застосована формула Тейлора:
,
де r n- так званий залишковий член або залишок ряду, його можна оцінити за допомогою формули Лагранжа:
, де число x укладено між х та а.
Правила введення функцій:
Якщо для деякого значення х r n→0 при n→∞, то в межі формула Тейлора перетворюється для цього значення на схожий ряд Тейлора:
,
Таким чином, функція f(x) може бути розкладена в ряд Тейлора в точці х, що розглядається, якщо:
1) вона має похідні всіх порядків;
2) побудований ряд сходиться у цій точці.
При а = 0 отримуємо ряд, званий поруч Маклорена:
,
Розкладання найпростіших (елементарних) функцій до ряду Маклорена:
Показові функції
, R=∞
Тригонометричні функції ![]() , R=∞
, R=∞ ![]() , R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Функція actgx не розкладається за ступенями x, т.к. ctg0=∞
Гіперболічні функції
Логарифмічні функції
, -1
Біноміальні ряди
![]() .
.
Приклад №1. Розкласти в статечний ряд функцію f(x)= 2x.
Рішення. Знайдемо значення функції та її похідних при х=0
f(x) = 2x, f( 0)
= 2 0
=1;
f"(x) = 2x ln2, f"( 0)
= 2 0
ln2 = ln2;
f""(x) = 2x ln 2 2, f""( 0)
= 2 0
ln 2 2 = ln 2 2;
…
f(n) (x) = 2x ln n 2, f(n) ( 0)
= 2 0
ln n 2 = ln n 2.
Підставляючи отримані значення похідних формулу ряду Тейлора, отримаємо:
Радіус збіжності цього ряду дорівнює нескінченності, тому дане розкладання справедливе для -∞<x<+∞.
Приклад №2. Написати ряд Тейлора за ступенями ( х+4) для функції f(x)= e x.
Рішення. Знаходимо похідні функції e xта їх значення у точці х=-4.
f(x)= е x, f(-4)
= е -4
;
f"(x)= е x, f"(-4)
= е -4
;
f""(x)= е x, f""(-4)
= е -4
;
…
f(n) (x)= е x, f(n) ( -4)
= е -4
.
Отже, шуканий ряд функції Тейлора має вигляд:
Дане розкладання також справедливе для -∞<x<+∞.
Приклад №3. Розкласти функцію f(x)=ln xв ряд за ступенями ( х- 1),
(Тобто в ряд Тейлора в околиці точки х=1).
Рішення. Знаходимо похідні цієї функції.
f(x)=lnx , , , ,
f(1)=ln1=0, f"(1)=1, f""(1)=-1, f""(1)=1*2,..., f(n) =(- 1) n-1 (n-1)!
Підставляючи ці значення формулу, отримаємо шуканий ряд Тейлора:
За допомогою ознаки Даламбер можна переконатися, що ряд сходиться при ½х-1½<1 . Действительно,
Ряд сходиться, якщо? х- 1½<1, т.е. при 0<x<2. При х=2 отримуємо ряд, що чергується, що задовольняє умовам ознаки Лейбніца. При х = 0 функція не визначена. Таким чином, областю збіжності ряду Тейлора є напіввідкритий проміжок (0; 2).
Приклад №4. Розкласти в статечний ряд функцію. Приклад №5. Розкласти до ряду Маклорена функцію. Зауваження
.
Цей метод заснований на теоремі про єдиність розкладання функції в статечний ряд. Сутність цієї теореми полягає в тому, що в околиці однієї і тієї ж точки не може бути отримано два різні статечні ряди, які б сходилися до однієї і тієї ж функції, яким би способом її розкладання не проводилося. Приклад №5а. Розкласти в ряд функцію Маклорена , вказати область збіжності. Дроб 3/(1-3x) можна як суму нескінченно спадної геометричної прогресії знаменником 3x, якщо |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
Приклад №6. Розкласти функцію до ряду Тейлора навколо точки х =3. Приклад №7. Написати ряд Тейлора за ступенями (х-1) функції ln(x+2). Приклад №8. Розкласти функцію f(x)=sin(πx/4) до ряду Тейлора навколо точки x =2. Приклад №1. Обчислити ln(3) з точністю до 0,01. Приклад №2. Вирахувати з точністю до 0,0001. Приклад №3. Обчислити інтеграл ∫ 0 1 4 sin (x) x з точністю до 10 -5 . Приклад №4. Обчислити інтеграл ∫ 0 1 4 e x 2 з точністю до 0,001. Розкладання функції в ряд Тейлора, Маклорена та Лорана на сайт для тренування практичних навичок. Це розкладання функції у ряд дає уявлення математикам оцінити наближене значення функції у певній точці області її визначення. Набагато простіше обчислити таке значення функції, порівняно із застосуванням таблиці Бредіса, так неактуальною у вік обчислювальної техніки. У ряд Тейлора розкласти функцію означає обчислити коефіцієнти перед лінійними функціями цього й записати це у правильному вигляді. Плутають студенти ці два ряди, не розуміючи, що є спільним випадком, а що окремим випадком другого. Нагадуємо раз і назавжди, ряд Маклорена - окремий випадок ряду Тейлорівського, тобто це і є ряд Тейлора, але в точці x = 0. Всі короткі записи розкладання відомих функцій, таких як e^x, Sin(x), Cos(x) та інші, це і є розкладання до ряду Тейлора, але у точці 0 для аргументу. Для функцій комплексного аргументу ряд Лоран є найчастішим завданням у ТФКП, оскільки представляє двосторонній нескінченний ряд. Він є сумою двох рядів. Ми пропонуємо вам переглянути приклад розкладання прямо на сайті сайт, це зробити дуже просто, натиснувши на "Приклад" з будь-яким номером, а потім кнопку "Рішення". Саме такому розкладанню функції в ряд зіставлений ряд, що мажорує, що обмежує функцію вихідну в деякій області по осі ординат, якщо змінна належить області абсцис. Векторного аналізу постачається порівняно інша цікава дисципліна в математиці. Оскільки досліджувати потрібно кожне доданок, необхідно досить багато часу на процес. Будь-якому ряду Тейлора можна порівняти ряд Маклорена, замінивши x0 на нуль, тоді як по ряду Маклорена часом очевидно уявлення ряду Тейлора назад. Як би це не потрібно робити в чистому вигляді, але цікаво для загального саморозвитку. Кожному ряду Лорана відповідає двосторонній нескінченний статечний ряд за цілими ступенями z-a, тобто ряд типу того ж Тейлора, але трохи відрізняється обчисленням коефіцієнтів. Про область збіжності низки Лорана розповімо трохи згодом, після кількох теоретичних викладок. Як і в минулому столітті, поетапного розкладання функції в ряд навряд чи можна досягти лише приведенням доданків до спільного знаменника, оскільки функції в знаменниках нелінійні. Наближене обчислення функціонального значення потребує встановлення завдань. Задумайтеся над тим, що коли аргумент ряду Тейлора є лінійна змінна, то розкладання відбувається в кілька дій, але зовсім інша картина, коли в якості аргументу функції, що розкладається, виступає складна або нелінійна функція, тоді очевидний процес представлення такої функції в статечний ряд, оскільки, таким чином, легко обчислити, нехай і наближене, але значення в будь-якій точці області визначення з мінімальною похибкою, що мало впливає на подальші розрахунки. Це стосується й низки Маклорена. коли необхідно обчислити функцію в нульовій точці. Однак сам ряд Лорана тут представлений розкладанням на площині з уявними одиницями. Також не без успіху буде правильне вирішення завдання під час загального процесу. У математиці такого підходу не знають, але він існує об'єктивно. В результаті ви можете дійти висновку так званих крапкових підмножин, і в розкладанні функції в ряд потрібно застосовувати відомі для цього процесу методи, такі як теорія похідних. Зайвий раз переконуємось у правоті вчителя, який зробив свої припущення з приводу підсумків пост обчислювальних викладок. Давайте відзначимо, що ряд Тейлора, отриманий за всіма канонами математики, існує і визначений на всій числовій осі, однак, шановні користувачі сервісу сайт, не забувайте про вид вихідної функції, адже може вийти так, що спочатку необхідно встановити область визначення функції, тобто виписати та виключити з подальших розглядів ті точки, за яких функція не визначена в ділянці дійсних чисел. Це покаже вашу спритність при вирішенні завдання. Не винятком висловленого буде й побудова низки Маклорена з нульовим значенням аргументу. Процес знаходження області визначення функції ніхто при цьому не скасовував, і ви повинні підійти з усією серйозністю до цієї математичної дії. У разі змісту поруч Лорана головної частини, параметр "a" називатиметься ізольованою особливою точкою, і ряд Лорана буде розкладений у кільці - це перетин областей збіжності його частин, звідси слідуватиме відповідна теорема. Але не все так складно, як може здатися на перший погляд недосвідченому студенту. Вивчивши якраз ряд Тейлора, можна легко зрозуміти ряд Лорана - узагальнений випадок розширення простору чисел. Будь-яке розкладання функції в ряд можна проводити лише у точці області визначення функції. Слід враховувати властивості таких функцій, наприклад, як періодичність чи нескінченна диференційність. Також пропонуємо вам скористатися таблицею готових розкладів у ряд Тейлора елементарних функцій, оскільки одна функція може бути представлена до десятків відмінних від одного статечних рядів, що можна бачити із застосування нашого калькулятора онлайн. Онлайн ряд Маклорена простіше простого визначити, якщо скористатися унікальним сервісом сайт, вам достатньо лише ввести правильну записану функцію і подану відповідь отримаєте за лічені секунди, він буде гарантовано точним і в стандартно записаному вигляді. Можете переписати результат одразу в чистовик на здачу викладачеві. Правильно спочатку визначити аналітичність розглянутої функції в кільцях, а потім однозначно стверджувати, що вона розкладена в ряд Лорана у всіх таких кільцях. Важливий момент щоб не випустити з виду членів ряду Лорана, що містять негативних ступенів. На цьому зосередьтеся якнайсильніше. Використовуйте теорему Лорана про розкладання функції в ряд за цілими ступенями. Теоретично функціональних рядів центральне місце займає розділ, присвячений розкладу функції ряд. Таким чином, ставиться завдання: за заданою функцією
потрібно знайти такий статечний ряд який на деякому інтервалі сходився і його сума дорівнювала Це завдання називається завданням розкладання функції в статечний ряд. Необхідною умовою розкладності функції в статечний рядє її диференційованість нескінченне число разів – це випливає з властивостей статечних рядів, що сходяться. Така умова виконується, зазвичай, для елементарних функцій у сфері визначення. Отже, припустимо, що функція Припустимо, що функцію де а 0 ,а 1 ,а 2 ,...,а п ,...
– невизначені (поки що) коефіцієнти. Покладемо у рівності (*) значення х = х 0 ,
тоді отримаємо Продиференціюємо статечний ряд (*) почленно і вважаючи тут х = х 0 ,
отримаємо При наступному диференціюванні отримаємо ряд вважаючи х = х 0 ,
отримаємо Після п-кратного диференціювання отримаємо Вважаючи в останній рівності х = х 0 ,
отримаємо Отже, коефіцієнти знайдено підставляючи які в ряд (*), отримаємо Отриманий ряд називається поряд Тейлора
для функції
Таким чином, ми встановили, що якщо функцію можна розкласти в статечний ряд за ступенями (х - х 0 ), то це розкладання єдино і отриманий ряд обов'язково є поряд Тейлора. Зауважимо, що ряд Тейлора можна отримати для будь-якої функції, що має похідні будь-якого порядку в точці х = х 0 .
Але це ще означає, що з функцією і отриманим поруч можна поставити знак рівності, тобто. що сума ряду дорівнює вихідній функції. По-перше, така рівність може мати сенс тільки в області збіжності, а отриманий для функції ряд Тейлора може і розходитися, по-друге, якщо ряд Тейлора буде сходитися, його сума може не збігатися з вихідною функцією. Сформулюємо твердження, за допомогою якого буде вирішено поставлене завдання. Якщо функція
деR n (х)-залишковий член формули Тейлора – має вигляд (форма Лагранжа) де
крапкаξ
лежить між х і х 0 . Зазначимо, що між Тейлора і формулою Тейлора є відмінність: формула Тейлора є кінцеву суму, тобто. п -фіксоване число. Нагадаємо, що сума ряду S(x)
може бути визначена як межа функціональної послідовності часткових сум S п (x)
на деякому проміжку Х: Відповідно до цього, розкласти функцію в ряд Тейлора означає знайти такий ряд, що для будь-якого хX Запишемо формулу Тейлора у вигляді, де Зауважимо, що Якщо Тим самим ми довели критерій розкладності функції до ряду Тейлора.
Для того, щоб у деякому проміжку функціяf(х) розкладалася в ряд Тейлора, необхідно і достатньо, щоб на цьому проміжку
За допомогою сформульованого критерію можна отримати достатніумови розкладності функції до ряду Тейлора.
Якщо вдеякої околиці точки х 0 абсолютні величини всіх похідних функції обмежені одним і тим самим числом М≥ 0, тобто. З вищевикладеного випливає алгоритмрозкладання функції
f(x) у ряд Тейлорана околиці точки х 0 :
1.
Знаходимо похідні функції f(x):
f(x), f'(x), f”(x), f”(x), f (n) (x),… 2. Обчислюємо значення функції та значення її похідних у точці х 0 f(x 0
), f'(x 0
), f”(x 0
), f'”(x 0
), f (n) (x 0
),…
3. Формально записуємо ряд Тейлора і знаходимо область збіжності отриманого статечного ряду. 4. Перевіряємо виконання достатніх умов, тобто. встановлюємо, для яких хз області збіжності, залишковий член R n (x)
прагне до нуля при Розкладання функцій у ряд Тейлора за цим алгоритмом називають розкладанням функції до ряду Тейлора за визначеннямабо безпосереднім розкладанням. Серед функціональних рядів найважливіше місце займають статечні ряди. Ступіньним рядом називають ряд члени якого – статечні функції, розташовані за зростаючим цілим невід'ємним ступенем x, а c0
, c 1
, c 2
, c n
- Постійні величини. Числа c1
, c 2
, c n
- Коефіцієнти членів ряду, c0
- Вільний член. Члени статечного ряду визначені на всій числовій прямій. Ознайомимося із поняттям області збіжності статечного ряду.
Це безліч значень змінної xдля яких ряд сходиться. Ступінні ряди мають досить просту область збіжності. Для дійсних значень змінної xобласть збіжності складається з однієї точки, або є деяким інтервалом (інтервалом збіжності), або збігається з усією віссю Ox
. При підстановці в степеневий ряд значення x= 0 вийде числовий ряд c0
+0+0+...+0+...
, що сходиться. Отже, при x= 0 сходиться будь-який статечний ряд і, отже, область його збіжності
не може бути порожнім безліччю. Структура області збіжності всіх статечних рядів однакова. Її можна встановити за допомогою наступної теореми. Теорема 1 (теорема Абеля). Якщо статечний ряд сходиться при певному значенні x = x 0
, Відмінному від нуля, то він сходиться, і до того ж абсолютно, при всіх значеннях |x| < |x 0
|
. Зверніть увагу: і відправне значення "ікс нульове" та будь-яке значення "ікса", яке порівнюється з відправним, взяті за модулем - без урахування знака. Слідство. Якщо статечний ряд розходиться
при деякому значенні x = x 1
, то він розходиться і за всіх значень |x| > |x 1
|
. Як ми вже з'ясували раніше, будь-який статечний ряд сходиться при значенні x= 0. Є статечні ряди, які сходяться тільки за x= 0 і розходяться за інших значеннях х. Виключаючи з розгляду цей випадок, припустимо, що статечний ряд сходиться при деякому значенні x = x 0
, Відмінний від нуля. Тоді, за теоремою Абеля, він сходить у всіх точках інтервалу ]-| x0
|, |x 0
|[
(інтервалу, лівою та правою межами якого є значення ікса, при якому статечний ряд сходиться, взяті відповідно зі знаком мінус і зі знаком плюс), симетричного щодо початку координат. Якщо ж статечний ряд розходиться за деякого значення x = x 1
, то на підставі слідства з теореми Абеля він розходиться і в усіх точках поза відрізком [-| x1
|, |x 1
|]
. Звідси випливає, що для будь-якого статечного ряду є інтервал , симетричний щодо початку координат, званий інтервалом збіжності
, у кожній точці якого ряд сходиться, на межах може сходитися, а може і розходитися, причому не обов'язково одночасно, а поза відрізком ряд розходиться. Число Rназивається радіусом збіжності статечного ряду. У окремих випадках інтервал збіжності статечного ряду
може вироджуватися в крапку (тоді ряд сходиться тільки за x= 0 і вважається, що R= 0) або являти собою всю числову пряму (тоді ряд сходить у всіх точках числової прямої і вважається, що). Таким чином, визначення області збіжності статечного ряду полягає у визначенні його радіусу збіжності
Rта дослідженні збіжності низки на межах інтервалу збіжності (при ). Теорема 2.Якщо всі коефіцієнти статечного ряду, починаючи з деякого, відмінні від нуля, його радіус збіжності дорівнює межі за відношення абсолютних величин коефіцієнтів загального наступного його членів низки, тобто. Приклад 1. Знайти область збіжності статечного ряду Рішення. Тут Використовуючи формулу (28), знайдемо радіус збіжності цього ряду: Досліджуємо збіжність ряду на кінцях інтервалу збіжності. У прикладі 13 показано, що даний ряд сходиться при x= 1 і розходиться за x= -1. Отже, областю збіжності є напівінтервал . Приклад 2. Знайти область збіжності статечного ряду Рішення. Коефіцієнти ряду позитивні, причому Знайдемо межу цього, тобто. радіус збіжності статечного ряду: Досліджуємо збіжність ряду на кінцях інтервалу. Підстановка значень x= -1/5 та x= 1/5 у цей ряд дає: Перший із цих рядів сходиться (див. приклад 5). Але тоді з теореми параграфа «Абсолютна збіжність» сходиться і другий ряд, а область його збіжності – відрізок Приклад 3. Знайти область збіжності статечного ряду Рішення. Тут За формулою (28) знаходимо радіус збіжності ряду: Досліджуємо збіжність ряду при значеннях. Підставивши їх у цей ряд, відповідно отримаємо Обидва ряду розходяться, оскільки не виконується необхідна умова збіжності (їх спільні члени не прагнуть нуля при ). Отже, обох кінцях інтервалу збіжності цей ряд розходиться, а область його збіжності – інтервал . Приклад 5. Знайти область збіжності статечного ряду Рішення. Знаходимо відношення , де , Відповідно до формули (28) радіус збіжності даного ряду тобто ряд сходиться тільки за x= 0 і розходиться за інших значеннях х. Приклади показують, що на кінцях інтервалу збіжності ряди поводяться по-різному. У прикладі 1 одному кінці інтервалу збіжності ряд сходиться, але в іншому – розходиться, у прикладі 2 – обох кінцях сходиться, у прикладі 3 – обох кінцях розходиться. Формула радіуса збіжності статечного ряду отримана у припущенні, що це коефіцієнти членів ряду, починаючи з деякого, відмінні від нуля. Тому застосування формули (28) припустимо лише у випадках. Якщо ця умова порушується, то радіус збіжності статечного ряду слід шукати за допомогою ознаки Даламбера, або ж, зробивши заміну змінною, перетворенням ряду до виду, в якому зазначена умова виконується. Приклад 6. Знайти інтервал збіжності статечного ряду Рішення. Цей ряд не містить членів з непарними ступенями х. Тому перетворимо ряд, вважаючи . Тоді отримаємо ряд для знаходження радіусу збіжності якого можна застосувати формулу (28). Так як , а , то радіус збіжності цього ряду З рівності отримуємо, отже, цей ряд сходиться на інтервалі. Нехай для статечного ряду радіус збіжності R> 0, тобто. цей ряд сходиться на інтервалі. Тоді кожному значенню хз інтервалу збіжності відповідає деяка сума низки. Отже, сума статечного ряду є функцією від хна інтервалі збіжності. Позначаючи її через f(x), можемо записати рівність розуміючи його в тому сенсі, що сума ряду в кожній точці хз інтервалу збіжності дорівнює значенню функції f(x) у цій точці. У цьому ж сенсі говоритимемо, що статечний ряд (29) сходить до функції f(x) на інтервалі збіжності. Поза інтервалом збіжності рівність (30) немає сенсу. Приклад 7.Знайти суму суму статечного ряду Рішення. Це геометричний ряд, у якого a= 1, а q= x. Отже, його сума є функцією справедливо лише для значень, хоча функція Можна довести, що сума статечного ряду f(x) безперервна та диференційована на будь-якому відрізку всередині інтервалу збіжності, зокрема в будь-якій точці інтервалу збіжності ряду. Наведемо теореми про почленное диференціювання та інтегрування статечних рядів. Теорема 1.Ступіньовий ряд (30) в інтервалі його збіжності можна почленно диференціювати необмежену кількість разів, причому статечні ряди, що виходять при цьому, мають той же радіус збіжності, що вихідний ряд, а суми їх відповідно рівні . Теорема 2.Ступіньовий ряд (30) можна необмежену кількість разів почленно інтегрувати в межах від 0 до х, якщо , причому виходять при цьому статечні ряди мають той же радіус збіжності, що і вихідний ряд, а суми відповідно рівні Нехай дана функція f(x), яку потрібно розкласти у статечний ряд, тобто. представити у вигляді (30): Завдання полягає у визначенні коефіцієнтів ……………………………………………….. (31) Вважаючи в рівності (30) і (31) х= 0, знаходимо Підставляючи знайдені вирази на рівність (30), отримаємо Знайдемо розкладання до ряду Маклорена деяких елементарних функцій. Приклад 8.Розкласти в ряд функцію Маклорена Рішення. Похідні цієї функції збігаються із самою функцією: Тому при х= 0 маємо Підставляючи ці значення формулу (32), отримаємо шукане розкладання: Цей ряд сходиться на всій числовій прямій (його радіус збіжності).
Рішення. У розкладанні (1) замінюємо х на -х 2 отримуємо:
, -∞
Рішення. Маємо
Користуючись формулою (4), можемо записати:
підставляючи замість х у формулу -х, отримаємо:
Звідси знаходимо: ln(1+x)-ln(1-x) = -
Розкриваючи дужки, переставляючи члени ряду та роблячи приведення подібних доданків, отримаємо
. Цей ряд сходиться в інтервалі (-1;1), оскільки він отриманий із двох рядів, кожен з яких сходиться в цьому інтервалі.
Формулами (1)-(5) можна й для розкладання відповідних функцій до ряду Тейлора, тобто. для розкладання функцій за цілими позитивними ступенями ( х-а). Для цього над заданою функцією необхідно зробити такі тотожні перетворення, щоб отримати одну з функцій (1)-(5), в якій замість хстоїть k( х-а) m, де k - постійне число, m - ціле позитивне число. Часто при цьому зручно зробити заміну змінною t=х-аі розкладати отриману функцію щодо t ряд Маклорена.
Рішення. Спочатку знайдемо 1-x-6x2=(1-3x)(1+2x) , .
на елементарні:
з областю збіжності | x |< 1/3.
Рішення. Це завдання можна вирішити, як і раніше, за допомогою визначення ряду Тейлора, для чого потрібно знайти похідні функції та їх значення при х=3. Однак простіше буде скористатися наявним розкладанням (5):
=
Отриманий ряд сходиться за або –3
Рішення.
Ряд сходиться при , або -2< x < 5.
Рішення. Зробимо заміну t=х-2:
Скориставшись розкладанням (3), у якому на місце х підставимо π/4 t, отримаємо:
Отриманий ряд сходить до заданої функції при -∞< π / 4 t<+∞, т.е. при (-∞
, (-∞Наближені обчислення за допомогою статечних рядів
Ступінні ряди широко використовуються в наближених обчисленнях. З їхньою допомогою із заданою точністю можна обчислювати значення коренів, тригонометричних функцій, логарифмів чисел, певних інтегралів. Ряди застосовуються також за інтегруванні диференціальних рівнянь.
Розглянемо розкладання функції в статечний ряд:
Для того щоб обчислити наближене значення функції в заданій точці х, що належить області збіжності зазначеного ряду, у її розкладанні залишають перші nчленів ( n- Кінцеве число), а інші доданки відкидають:
Для оцінки похибки наближеного значення необхідно оцінити відкинутий залишок r n (x) . Для цього застосовують такі прийоми:
Рішення. Скористаємося розкладанням , де x=1/2 (див. приклад 5 у попередній темі):
Перевіримо, чи можемо ми відкинути залишок після перших трьох членів розкладання, для цього оцінимо його за допомогою суми геометричної прогресії, що нескінченно спадає:
Таким чином, ми можемо відкинути цей залишок та отримуємо
Рішення. Скористаємося біноміальним рядом. Оскільки 5 3 є найближчим до 130 кубом цілого числа, то доцільно число 130 у вигляді 130=5 3 +5. 
тому що вже четвертий член отриманого ряду, що чергується, задовольняє ознакою Лейбніца, менше необхідної точності:
Тому його і наступні за ним члени можна відкинути.
Багато практично потрібні певні чи невласні інтеграли неможливо знайти обчислені з допомогою формули Ньютона-Лейбніца, оскільки її застосування пов'язані з перебуванням первісної, часто має вирази в елементарних функціях. Буває також, що знаходження первісної можливе, але надмірно трудомістке. Однак якщо підінтегральна функція розкладається в статечний ряд, а межі інтегрування належать інтервалу збіжності цього ряду, то можливе наближене обчислення інтеграла з заданою точністю.
Рішення. Відповідний невизначений інтеграл може бути виражений в елементарних функціях, тобто. є «інтеграл, що не береться». Застосувати формулу Ньютона-Лейбніца тут не можна. Обчислимо інтеграл приблизно.
Розділивши почленно ряд для sin xна x, Отримаємо: 
Інтегруючи цей ряд почленно (це можливо, оскільки межі інтегрування належать інтервалу збіжності даного ряду), отримуємо:
Так як отриманий ряд задовольняє умовам Лейбніца і достатньо взяти суму перших двох членів, щоб отримати потрібне значення із заданою точністю.
Таким чином, знаходимо  .
.
Рішення.

![]() . Перевіримо, чи можемо ми залишити залишок після другого члена отриманого ряду.
. Перевіримо, чи можемо ми залишити залишок після другого члена отриманого ряду.
0.0001<0.001. Следовательно,  .
. ,
тобто.
,
тобто. =
..
=
..
 має похідні будь-якого порядку. Чи можна її розкласти в статечний ряд, якщо можна, то як знайти цей ряд? Найпростіше вирішується друга частина завдання, з неї і почнемо.
має похідні будь-якого порядку. Чи можна її розкласти в статечний ряд, якщо можна, то як знайти цей ряд? Найпростіше вирішується друга частина завдання, з неї і почнемо. можна подати у вигляді суми статечного ряду, що сходиться в інтервалі, що містить точку х 0 :
можна подати у вигляді суми статечного ряду, що сходиться в інтервалі, що містить точку х 0 :
 =
..
(*)
=
..
(*) .
. =
..
=
..
 .
. =
..
=
..
 , звідки
, звідки  .
. , звідки
, звідки
 ,
,
 ,
,
 ,
…,
,
…,
 ,….,
,…., .
.
3.2. Достатні умови розкладності функції до ряду Тейлора
 в деякій околиці точки х 0 має похідні до (n+
1)-го порядку включно, то в цій околиці має місцеформула
Тейлора
в деякій околиці точки х 0 має похідні до (n+
1)-го порядку включно, то в цій околиці має місцеформула
Тейлора

 .
.
 визначає ту помилку, яку ми отримуємо, замінюй функцію f(x)
багаточленом S n (x).
визначає ту помилку, яку ми отримуємо, замінюй функцію f(x)
багаточленом S n (x).
 , то
, то  ,Тобто. функція розкладається на ряд Тейлора. Інакше, якщо
,Тобто. функція розкладається на ряд Тейлора. Інакше, якщо  , то
, то  .
. , деR n (x) - Залишковий член ряду Тейлора.
, деR n (x) - Залишковий член ряду Тейлора. , тпро цю околицю функція розкладається на ряд Тейлора.
, тпро цю околицю функція розкладається на ряд Тейлора. або
або
 .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]() :
:![]()
![]() ,
,![]()
![]()
![]()
Сума статечного ряду. Диференціювання та інтегрування статечних рядів
![]()
![]() . Ряд сходиться, якщо , а - його інтервал збіжності. Тому рівність
. Ряд сходиться, якщо , а - його інтервал збіжності. Тому рівність![]()
![]() визначено для всіх значень хкрім х= 1.
визначено для всіх значень хкрім х= 1.
Розкладання функцій у статечні ряди
![]() ряду (30). Для цього, диференціюючи рівність (30) почленно, послідовно знайдемо:
ряду (30). Для цього, диференціюючи рівність (30) почленно, послідовно знайдемо:![]()
![]()

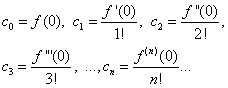
 (32)
(32)
![]() (33)
(33)

