Jak obliczyć pole równoległościanu. Powierzchnia boczna różnych piramid

Przygotowując się do Unified State Exam z matematyki, uczniowie muszą usystematyzować swoją wiedzę z algebry i geometrii. Chciałbym połączyć wszystkie znane informacje, na przykład, jak obliczyć pole piramidy. Co więcej, zaczynając od podstawy i krawędzi bocznych, aż po całą powierzchnię. Jeśli sytuacja ze ścianami bocznymi jest jasna, ponieważ są to trójkąty, wówczas podstawa jest zawsze inna.

Jak znaleźć obszar podstawy piramidy?

Może to być absolutnie dowolna figura: od dowolnego trójkąta po n-gon. A ta podstawa, oprócz różnicy w liczbie kątów, może być figurą regularną lub nieregularną. W zadaniach egzaminu Unified State Exam, które interesują uczniów, znajdują się tylko zadania z prawidłowymi liczbami u podstawy. Dlatego porozmawiamy tylko o nich.

Zwykły trójkąt

Czyli równoboczny. Taki, w którym wszystkie strony są równe i są oznaczone literą „a”. W tym przypadku pole podstawy piramidy oblicza się według wzoru:

S = (a 2 * √3) / 4.

Kwadrat

Wzór na obliczenie jego powierzchni jest najprostszy, tutaj „a” jest znowu bokiem:

Dowolny regularny n-gon

Bok wielokąta ma takie samo oznaczenie. Do liczby kątów używana jest łacińska litera n.

S = (n * a 2) / (4 * tg (180°/n)).

Co zrobić przy obliczaniu powierzchni bocznej i całkowitej?

Ponieważ podstawą jest figura regularna, wszystkie ściany piramidy są równe. Co więcej, każdy z nich jest trójkątem równoramiennym, ponieważ krawędzie boczne są równe. Następnie, aby obliczyć pole boczne piramidy, będziesz potrzebować wzoru składającego się z sumy identycznych jednomianów. Liczbę wyrazów określa liczba boków podstawy.

Pole trójkąta równoramiennego oblicza się ze wzoru, w którym połowa iloczynu podstawy jest mnożona przez wysokość. Ta wysokość w piramidzie nazywa się apothem. Jego oznaczenie to „A”. Ogólny wzór na pole powierzchni bocznej to:

S = ½ P*A, gdzie P jest obwodem podstawy piramidy.

Zdarzają się sytuacje, gdy nie są znane boki podstawy, ale podane są krawędzie boczne (c) i kąt płaski na jej wierzchołku (α). Następnie należy skorzystać z następującego wzoru, aby obliczyć pole boczne piramidy:

S = n/2 * in 2 sin α .

Zadanie nr 1

Stan : schorzenie. Znajdź całkowite pole piramidy, jeśli jej podstawa ma bok 4 cm, a apotem ma wartość √3 cm.

Rozwiązanie. Musisz zacząć od obliczenia obwodu podstawy. Ponieważ jest to regularny trójkąt, to P = 3*4 = 12 cm Ponieważ apotem jest znany, możemy od razu obliczyć pole całej powierzchni bocznej: ½*12*√3 = 6√3 cm 2.

Dla trójkąta u podstawy otrzymujemy następującą wartość pola: (4 2 *√3) / 4 = 4√3 cm 2.

Aby wyznaczyć całą powierzchnię, należy dodać dwie otrzymane wartości: 6√3 + 4√3 = 10√3 cm 2.

Odpowiedź. 10√3 cm 2.

Problem nr 2

Stan. Istnieje regularna czworokątna piramida. Długość boku podstawy wynosi 7 mm, krawędź boku 16 mm. Konieczne jest sprawdzenie jego powierzchni.

Rozwiązanie. Ponieważ wielościan jest czworokątny i regularny, jego podstawą jest kwadrat. Kiedy już poznasz pole podstawy i ścian bocznych, będziesz mógł obliczyć pole piramidy. Wzór na kwadrat podano powyżej. A w przypadku ścian bocznych znane są wszystkie boki trójkąta. Dlatego możesz użyć wzoru Herona do obliczenia ich pól.

Pierwsze obliczenia są proste i prowadzą do następującej liczby: 49 mm 2. Dla drugiej wartości musisz obliczyć półobwód: (7 + 16*2): 2 = 19,5 mm. Teraz możesz obliczyć pole trójkąta równoramiennego: √(19,5*(19,5-7)*(19,5-16) 2) = √2985,9375 = 54,644 mm 2. Istnieją tylko cztery takie trójkąty, więc przy obliczaniu ostatecznej liczby należy ją pomnożyć przez 4.

Okazuje się: 49 + 4 * 54,644 = 267,576 mm 2.

Odpowiedź. Pożądana wartość to 267,576 mm2.

Problem nr 3

Stan. W przypadku regularnej czworokątnej piramidy należy obliczyć powierzchnię. Wiadomo, że bok kwadratu ma długość 6 cm, a wysokość 4 cm.

Rozwiązanie. Najłatwiej jest użyć wzoru na iloczyn obwodu i apotema. Pierwszą wartość łatwo znaleźć. Drugie jest trochę bardziej skomplikowane.

Będziemy musieli pamiętać o twierdzeniu Pitagorasa i rozważyć Jest ono utworzone przez wysokość piramidy i apothem, czyli przeciwprostokątną. Druga noga jest równa połowie boku kwadratu, ponieważ wysokość wielościanu przypada na jego środek.

Wymagany apotem (przeciwprostokątna trójkąta prostokątnego) jest równy √(3 2 + 4 2) = 5 (cm).

Teraz możesz obliczyć wymaganą wartość: ½*(4*6)*5+6 2 = 96 (cm 2).

Odpowiedź. 96cm2.

Problem nr 4

Stan : schorzenie. Podano prawidłowy bok: boki podstawy mają długość 22 mm, krawędzie boczne 61 mm. Jaka jest powierzchnia boczna tego wielościanu?

Rozwiązanie. Rozumowanie w nim jest takie samo jak opisane w zadaniu nr 2. Tylko tam dano piramidę z kwadratem u podstawy, a teraz jest to sześciokąt.

W pierwszej kolejności pole podstawy obliczamy korzystając z powyższego wzoru: (6*22 2) / (4*tg (180°/6)) = 726/(tg30°) = 726√3 cm 2.

Teraz musisz znaleźć półobwód trójkąta równoramiennego, który jest ścianą boczną. (22+61*2):2 = 72 cm Pozostaje tylko obliczyć pole każdego takiego trójkąta ze wzoru Herona, a następnie pomnożyć je przez sześć i dodać do otrzymanego dla podstawy.

Obliczenia z wykorzystaniem wzoru Herona: √(72*(72-22)*(72-61) 2)=√435600=660 cm 2. Obliczenia, które dadzą powierzchnię boczną: 660 * 6 = 3960 cm 2. Pozostaje je dodać, aby znaleźć całą powierzchnię: 5217,47≈5217 cm 2.

Odpowiedź. Podstawa ma długość 726√3 cm 2, powierzchnia boczna 3960 cm 2, a całe pole wynosi 5217 cm 2.

Cylinder to figura składająca się z cylindrycznej powierzchni i dwóch równoległych okręgów. Obliczanie pola cylindra jest problemem w geometrycznej gałęzi matematyki, który można rozwiązać po prostu. Metod jego rozwiązania jest kilka, które ostatecznie zawsze sprowadzają się do jednego wzoru.

Jak znaleźć pole cylindra - zasady obliczeń

• Aby obliczyć powierzchnię cylindra, należy dodać dwa obszary podstawy do pola powierzchni bocznej: S = Sside + 2Sbase. W bardziej szczegółowej wersji wzór ten wygląda następująco: S= 2 π rh+ 2 π r2= 2 π r(h+ r).
• Pole powierzchni bocznej danej bryły geometrycznej można obliczyć, jeśli znana jest jej wysokość i promień okręgu leżącego u jej podstawy. W tym przypadku możesz wyrazić promień z obwodu, jeśli został podany. Wysokość można znaleźć, jeśli w warunku podana jest wartość generatora. W tym przypadku tworząca będzie równa wysokości. Wzór na powierzchnię boczną tego ciała wygląda następująco: S= 2 π rh.
• Pole podstawy oblicza się za pomocą wzoru na znalezienie pola koła: S osn= π r 2 . W niektórych przypadkach promień może nie zostać podany, ale można podać obwód. Za pomocą tego wzoru promień można wyrazić dość łatwo. С=2π r, r= С/2π. Trzeba też pamiętać, że promień to połowa średnicy.
• Przy wykonywaniu wszystkich tych obliczeń liczba π zwykle nie jest przekładana na 3,14159... Wystarczy ją dodać obok wartości liczbowej uzyskanej w wyniku obliczeń.
• Następnie wystarczy pomnożyć znaleziony obszar podstawy przez 2 i dodać do otrzymanej liczby obliczony obszar powierzchni bocznej figury.
• Jeśli problem wskaże, że cylinder ma przekrój osiowy i jest prostokątem, to rozwiązanie będzie nieco inne. W tym przypadku szerokość prostokąta będzie średnicą okręgu leżącego u podstawy ciała. Długość figury będzie równa tworzącej lub wysokości cylindra. Konieczne jest obliczenie wymaganych wartości i zastąpienie ich znanym już wzorem. W takim przypadku szerokość prostokąta należy podzielić przez dwa, aby znaleźć pole podstawy. Aby znaleźć powierzchnię boczną, długość mnoży się przez dwa promienie i liczbę π.
• Pole danej bryły geometrycznej możesz obliczyć poprzez jej objętość. Aby to zrobić, należy wyprowadzić brakującą wartość ze wzoru V=π r 2 h.
• Obliczanie powierzchni cylindra nie jest skomplikowane. Wystarczy znać wzory i umieć z nich wyprowadzić wielkości niezbędne do przeprowadzenia obliczeń.

Powierzchnia piramidy. W tym artykule przyjrzymy się problemom związanym ze zwykłymi piramidami. Przypomnę, że regularna piramida to piramida, której podstawą jest foremny wielokąt, wierzchołek piramidy jest rzutowany na środek tego wielokąta.

Boczna ściana takiej piramidy jest trójkątem równoramiennym.Wysokość tego trójkąta wyciągniętego z wierzchołka regularnej piramidy nazywa się apothem, SF - apothem:

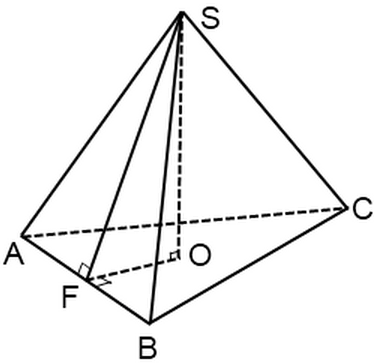
W zadaniu przedstawionym poniżej należy znaleźć pole powierzchni całej piramidy lub pole jej powierzchni bocznej. Na blogu omawialiśmy już kilka problemów związanych ze zwykłymi ostrosłupami, gdzie została poruszona kwestia znalezienia elementów (wysokość, krawędź podstawy, krawędź boczna).

Zadania Unified State Examination zazwyczaj badają regularne piramidy trójkątne, czworokątne i sześciokątne. Nie widziałem żadnych problemów z regularnymi piramidami pięciokątnymi i siedmiokątnymi.

Wzór na pole całej powierzchni jest prosty - trzeba znaleźć sumę pola podstawy piramidy i pola jej powierzchni bocznej:

Rozważmy zadania:

Boki podstawy regularnej czworokątnej piramidy wynoszą 72, krawędzie boczne wynoszą 164. Znajdź pole powierzchni tej piramidy.

Pole powierzchni piramidy jest równe sumie pól powierzchni bocznej i podstawy:

*Powierzchnia boczna składa się z czterech trójkątów o równych polach. Podstawą piramidy jest kwadrat.

Pole boku piramidy możemy obliczyć za pomocą:

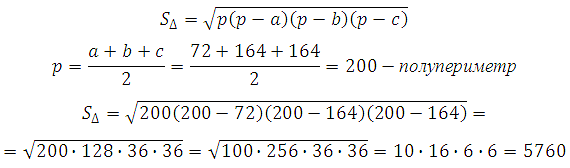
Zatem powierzchnia piramidy wynosi:

Odpowiedź: 28224

Boki podstawy regularnej sześciokątnej piramidy są równe 22, krawędzie boczne są równe 61. Znajdź pole powierzchni bocznej tej piramidy.

Podstawą regularnej piramidy sześciokątnej jest sześciokąt foremny.

Pole powierzchni bocznej tej piramidy składa się z sześciu obszarów równych trójkątów o bokach 61,61 i 22:

Znajdźmy obszar trójkąta, korzystając ze wzoru Herona:

Zatem pole powierzchni bocznej wynosi:

Odpowiedź: 3240

*W zadaniach przedstawionych powyżej pole powierzchni bocznej można obliczyć za pomocą innego wzoru na trójkąt, ale w tym celu należy obliczyć apotem.

27155. Znajdź pole powierzchni regularnej czworokątnej piramidy, której boki podstawy wynoszą 6 i których wysokość wynosi 4.

Aby znaleźć pole powierzchni piramidy, musimy znać pole podstawy i pole powierzchni bocznej:

Pole podstawy wynosi 36, ponieważ jest to kwadrat o boku 6.

Powierzchnia boczna składa się z czterech ścian, które są równymi trójkątami. Aby znaleźć pole takiego trójkąta, musisz znać jego podstawę i wysokość (apotem):

*Pole trójkąta jest równe połowie iloczynu podstawy i wysokości narysowanej do tej podstawy.

Podstawa jest znana, jest równa sześć. Znajdźmy wysokość. Rozważmy trójkąt prostokątny (zaznaczony na żółto):

Jedna noga jest równa 4, ponieważ jest to wysokość piramidy, druga jest równa 3, ponieważ jest równa połowie krawędzi podstawy. Przeciwprostokątną możemy znaleźć za pomocą twierdzenia Pitagorasa:

Oznacza to, że pole powierzchni bocznej piramidy wynosi:

Zatem powierzchnia całej piramidy wynosi:

Odpowiedź: 96

27069. Boki podstawy regularnej czworokątnej piramidy są równe 10, krawędzie boczne są równe 13. Znajdź pole powierzchni tej piramidy.

27070. Boki podstawy regularnej sześciokątnej piramidy są równe 10, krawędzie boczne są równe 13. Znajdź pole powierzchni bocznej tej piramidy.

Istnieją również wzory na pole powierzchni bocznej regularnej piramidy. W regularnej piramidzie podstawa jest rzutem prostopadłym powierzchni bocznej, zatem:

P- obwód podstawy, l- apotem piramidy

*Wzór ten opiera się na wzorze na pole trójkąta.

Jeśli chcesz dowiedzieć się więcej o tym, jak wyprowadzane są te formuły, nie przegap tego i śledź publikację artykułów.To wszystko. Powodzenia!

Z poważaniem, Aleksander Krutitskikh.

P.S: Byłbym wdzięczny, gdybyś powiedział mi o tej stronie w sieciach społecznościowych.

Cylinder to bryła geometryczna ograniczona dwiema równoległymi płaszczyznami i powierzchnią cylindryczną. W artykule porozmawiamy o tym, jak znaleźć pole cylindra i korzystając ze wzoru, rozwiążemy na przykład kilka problemów.

Cylinder ma trzy powierzchnie: górę, podstawę i powierzchnię boczną.

Góra i podstawa cylindra mają kształt okręgów i są łatwe do zidentyfikowania.

Wiadomo, że pole koła jest równe πr 2. Dlatego wzór na pole dwóch okręgów (góry i podstawy walca) będzie wynosił πr 2 + πr 2 = 2πr 2.

Trzecia, boczna powierzchnia cylindra, to zakrzywiona ściana cylindra. Aby lepiej wyobrazić sobie tę powierzchnię, spróbujmy ją przekształcić, aby uzyskać rozpoznawalny kształt. Wyobraź sobie, że cylinder to zwykła puszka, która nie ma górnej pokrywy ani dna. Zróbmy pionowe nacięcie na bocznej ścianie od góry do podstawy puszki (Krok 1 na rysunku) i spróbujmy maksymalnie otworzyć (wyprostować) powstałą figurę (Krok 2).

Po całkowitym otwarciu powstałego słoika zobaczymy znajomą figurę (krok 3), jest to prostokąt. Pole prostokąta jest łatwe do obliczenia. Ale zanim to wróćmy na chwilę do oryginalnego cylindra. Wierzchołek pierwotnego walca jest okręgiem, a wiemy, że obwód oblicza się ze wzoru: L = 2πr. Na rysunku jest on zaznaczony na czerwono.

Kiedy ścianka boczna cylindra jest całkowicie otwarta, widzimy, że obwód staje się długością powstałego prostokąta. Bokami tego prostokąta będzie obwód (L = 2πr) i wysokość walca (h). Pole prostokąta jest równe iloczynowi jego boków - S = długość x szerokość = L x h = 2πr x h = 2πrh. W rezultacie otrzymaliśmy wzór na obliczenie pola powierzchni bocznej cylindra.

Wzór na powierzchnię boczną cylindra
Strona S = 2πrh

Całkowita powierzchnia cylindra

Wreszcie, jeśli dodamy pole wszystkich trzech powierzchni, otrzymamy wzór na całkowitą powierzchnię walca. Pole powierzchni cylindra jest równe powierzchni górnej części cylindra + powierzchni podstawy cylindra + powierzchni bocznej cylindra lub S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Czasami wyrażenie to zapisuje się identycznie jak wzór 2πr (r + h).

Wzór na całkowitą powierzchnię cylindra
S = 2πr 2 + 2πrh = 2πr(r + h)
r – promień cylindra, h – wysokość cylindra

Przykłady obliczania pola powierzchni cylindra

Aby zrozumieć powyższe wzory, spróbujmy obliczyć pole powierzchni walca na przykładach.

1. Promień podstawy cylindra wynosi 2, wysokość wynosi 3. Określ pole powierzchni bocznej cylindra.

Powierzchnię całkowitą oblicza się ze wzoru: bok S. = 2πrh

Strona S = 2 * 3,14 * 2 * 3

Strona S = 6,28 * 6

Strona S = 37,68

Pole powierzchni bocznej cylindra wynosi 37,68.

2. Jak znaleźć powierzchnię walca, jeśli wysokość wynosi 4, a promień wynosi 6?

Powierzchnię całkowitą oblicza się ze wzoru: S = 2πr 2 + 2πrh

S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

jest figurą wieloaspektową, której podstawą jest wielokąt, a pozostałe ściany są reprezentowane przez trójkąty o wspólnym wierzchołku.

Jeśli podstawą jest kwadrat, wówczas nazywa się piramidę czworokątny, jeśli trójkąt – to trójkątny. Wysokość piramidy jest rysowana od jej wierzchołka prostopadle do podstawy. Służy również do obliczania powierzchni apotem– wysokość lica bocznego obniżonego od góry.
Wzór na pole powierzchni bocznej piramidy jest sumą pól jej ścian bocznych, które są sobie równe. Jednak ta metoda obliczeń jest stosowana bardzo rzadko. Zasadniczo obszar piramidy oblicza się na podstawie obwodu podstawy i apothemu:

Rozważmy przykład obliczenia pola powierzchni bocznej piramidy.

Niech będzie dana piramida o podstawie ABCDE i wierzchołku F. AB =BC =CD =DE =EA =3 cm Apothem a = 5 cm. Znajdź powierzchnię boczną piramidy.
Znajdźmy obwód. Ponieważ wszystkie krawędzie podstawy są równe, obwód pięciokąta będzie równy:
Teraz możesz znaleźć boczny obszar piramidy:

Obszar regularnej trójkątnej piramidy

Regularna trójkątna piramida składa się z podstawy, w której leży regularny trójkąt i trzech ścian bocznych o równych polach.
Wzór na pole powierzchni bocznej regularnej piramidy trójkątnej można obliczyć na różne sposoby. Możesz zastosować zwykły wzór obliczeniowy, używając obwodu i apothemu, lub możesz znaleźć obszar jednej twarzy i pomnożyć go przez trzy. Ponieważ ściana piramidy jest trójkątem, stosujemy wzór na pole trójkąta. Będzie to wymagało apothemu i długości podstawy. Rozważmy przykład obliczenia pola powierzchni bocznej regularnej trójkątnej piramidy.

Biorąc pod uwagę piramidę z apotemem a = 4 cm i powierzchnią podstawy b = 2 cm. Znajdź pole powierzchni bocznej piramidy.
Najpierw znajdź obszar jednej ze ścian bocznych. W tym przypadku będzie to:
Zastąp wartości we wzorze:
Ponieważ w zwykłej piramidzie wszystkie boki są takie same, pole powierzchni bocznej piramidy będzie równe sumie pól trzech ścian. Odpowiednio:

Obszar ściętej piramidy

Kadłubowy Piramida to wielościan utworzony przez piramidę, której przekrój jest równoległy do ​​podstawy.
Wzór na pole powierzchni bocznej ściętej piramidy jest bardzo prosty. Pole jest równe iloczynowi połowy sumy obwodów podstaw i apotemów: