Примери за определен интеграл по части. Решаване на интеграли онлайн
Преди това по дадена функция, ръководейки се от различни формули и правила, намерихме нейната производна. Производното има многобройни приложения: това е скоростта на движение (или по-общо, скоростта на всеки процес); ъгловият коефициент на допирателната към графиката на функцията; използвайки производната, можете да изследвате функция за монотонност и екстремуми; помага за решаването на проблеми с оптимизацията.
Но наред със задачата за намиране на скоростта по известен закон на движение, има и обратна задача - задачата за възстановяване на закона за движение по известна скорост. Нека разгледаме един от тези проблеми.
Пример 1.Материална точка се движи по права линия, нейната скорост в момент t се дава по формулата v=gt. Намерете закона за движение.
Решение. Нека s = s(t) е желаният закон на движение. Известно е, че s"(t) = v(t). Това означава, че за решаване на проблема трябва да изберете функция s = s(t), чиято производна е равна на gt. Не е трудно да се познае че \(s(t) = \frac(gt^ 2)(2) \).Всъщност
\(s"(t) = \left(\frac(gt^2)(2) \right)" = \frac(g)(2)(t^2)" = \frac(g)(2) \ cdot 2t = gt\)
Отговор: \(s(t) = \frac(gt^2)(2) \)
Нека веднага да отбележим, че примерът е решен правилно, но непълно. Получаваме \(s(t) = \frac(gt^2)(2) \). Всъщност проблемът има безкрайно много решения: всяка функция от вида \(s(t) = \frac(gt^2)(2) + C\), където C е произволна константа, може да служи като закон на движение, тъй като \(\left (\frac(gt^2)(2) +C \right)" = gt \)
За да направим проблема по-конкретен, трябваше да коригираме първоначалната ситуация: да посочим координатата на движеща се точка в даден момент от времето, например при t = 0. Ако, да речем, s(0) = s 0, тогава от равенство s(t) = (gt 2)/2 + C получаваме: s(0) = 0 + C, т.е. C = s 0. Сега законът на движението е еднозначно дефиниран: s(t) = (gt 2)/2 + s 0.
В математиката на взаимно обратните операции се дават различни имена, изобретени са специални обозначения, например: повдигане на квадрат (x 2) и квадратен корен (\(\sqrt(x) \)), синус (sin x) и арксинус (arcsin x) и т.н. Процесът на намиране на производната на дадена функция се нарича диференциация, а обратната операция, т.е. процесът на намиране на функция от дадена производна, е интеграция.
Самият термин „производна“ може да бъде оправдан „от ежедневни термини“: функцията y = f(x) „ражда“ нова функция y" = f"(x). Функцията y = f(x) действа като „родител“, но математиците, естествено, не я наричат „родител“ или „производител“; те казват, че е така по отношение на функцията y" = f"( x), първично изображение или примитив.
Определение.Функцията y = F(x) се нарича първоизводна за функцията y = f(x) на интервала X, ако равенството F"(x) = f(x) е валидно за \(x \in X\)
На практика интервалът X обикновено не се посочва, но се подразбира (като естествена област на дефиниране на функцията).
Да дадем примери.
1) Функцията y = x 2 е противопроизводна на функцията y = 2x, тъй като за всяко x е вярно равенството (x 2)" = 2x
2) Функцията y = x 3 е противопроизводна на функцията y = 3x 2, тъй като за всяко x е вярно равенството (x 3)" = 3x 2
3) Функцията y = sin(x) е антипроизводна за функцията y = cos(x), тъй като за всяко x равенството (sin(x))" = cos(x) е вярно
При намирането на антипроизводни, както и на производни, се използват не само формули, но и някои правила. Те са пряко свързани със съответните правила за изчисляване на деривати.
Знаем, че производната на една сума е равна на сумата от нейните производни. Това правило генерира съответното правило за намиране на антипроизводни.
Правило 1.Първопроизводната на сбор е равна на сбора на първопроизводните.
Знаем, че постоянният множител може да бъде изваден от знака на производната. Това правило генерира съответното правило за намиране на антипроизводни.
Правило 2.Ако F(x) е антипроизводно за f(x), тогава kF(x) е антипроизводно за kf(x).
Теорема 1.Ако y = F(x) е първоизводна за функцията y = f(x), тогава първоизводната за функцията y = f(kx + m) е функцията \(y=\frac(1)(k)F (kx+m) \)
Теорема 2.Ако y = F(x) е първоизводна за функцията y = f(x) на интервала X, тогава функцията y = f(x) има безкрайно много първоизводни и всички те имат формата y = F(x) + C.
Интеграционни методи
Метод на заместване на променливи (метод на заместване)
Методът на интегриране чрез заместване включва въвеждането на нова интеграционна променлива (т.е. заместване). В този случай даденият интеграл се свежда до нов интеграл, който е табличен или сводим към него. Няма общи методи за избор на замествания. Способността за правилно определяне на заместването се придобива чрез практика.
Нека е необходимо да се изчисли интегралът \(\textstyle \int F(x)dx \). Нека направим заместването \(x= \varphi(t) \), където \(\varphi(t) \) е функция, която има непрекъсната производна.
Тогава \(dx = \varphi " (t) \cdot dt \) и въз основа на свойството за инвариантност на формулата за интегриране за неопределения интеграл, получаваме формулата за интегриране чрез заместване:
\(\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt \)
Интегриране на изрази от формата \(\textstyle \int \sin^n x \cos^m x dx \)
Ако m е нечетно, m > 0, тогава е по-удобно да се направи заместването sin x = t.
Ако n е нечетно, n > 0, тогава е по-удобно да се направи заместването cos x = t.
Ако n и m са четни, тогава е по-удобно да се направи заместването tg x = t.
Интеграция по части
Интегриране по части - прилагане на следната формула за интегриране:
\(\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du \)
или:
\(\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx \)
Таблица с неопределени интеграли (антипроизводни) на някои функции
$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) +C \;\; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(arcsin) x +C $$ $$ \int \frac(dx)(1+x^2 ) = \text(arctg) x +C $$ $$ \int \text(ch) x dx = \text(sh) x +C $$ $$ \int \text(sh) x dx = \text(ch )x+C $$Интеграция по части. Примери за решения
Здравей отново. Днес в урока ще научим как да интегрираме по части. Методът на интегриране по части е един от крайъгълните камъни на интегралното смятане. По време на тестове или изпити студентите почти винаги са помолени да решават следните видове интеграли: най-простият интеграл (виж статията)или интеграл чрез замяна на променлива (виж статията)или интегралът просто е включен метод на интегриране по части.
Както винаги, трябва да имате под ръка: Таблица на интегралитеИ Таблица с производни. Ако все още ги нямате, моля, посетете хранилището на моя уебсайт: Математически формули и таблици. Няма да се уморя да повтарям - по-добре е да разпечатате всичко. Ще се опитам да представя целия материал последователно, просто и ясно, няма особени затруднения при интегрирането на частите.
Какъв проблем решава методът на интегриране по части? Методът на интегриране по части решава много важен проблем; той ви позволява да интегрирате някои функции, които не са в таблицата, работафункции, а в някои случаи – дори частни. Както си спомняме, няма удобна формула: ![]() . Но има и този:
. Но има и този: ![]() – формула за интегриране по части лично. Знам, знам, ти си единственият - ще работим с нея през целия урок (сега е по-лесно).
– формула за интегриране по части лично. Знам, знам, ти си единственият - ще работим с нея през целия урок (сега е по-лесно).
И веднага списъкът в студиото. Интегралите от следните видове се вземат по части:
1) , ![]() , – логаритъм, логаритъм, умножен по някакъв полином.
, – логаритъм, логаритъм, умножен по някакъв полином.
2) ,![]() е експоненциална функция, умножена по някакъв полином. Това включва и интеграли като - експоненциална функция, умножена по полином, но на практика това е 97 процента, под интеграла има хубава буква „e“. ... статията се оказва някак лирична, о, да ... пролетта дойде.
е експоненциална функция, умножена по някакъв полином. Това включва и интеграли като - експоненциална функция, умножена по полином, но на практика това е 97 процента, под интеграла има хубава буква „e“. ... статията се оказва някак лирична, о, да ... пролетта дойде.
3) , ![]() , са тригонометрични функции, умножени по някакъв полином.
, са тригонометрични функции, умножени по някакъв полином.
4) , – обратни тригонометрични функции („арки“), „арки“, умножени по някакъв полином.
Някои фракции също са взети на части; ние също ще разгледаме съответните примери подробно.
Интеграли от логаритми
Пример 1
Класически. От време на време този интеграл може да се намери в таблици, но не е препоръчително да използвате готов отговор, тъй като учителят има пролетен витаминен дефицит и ще ругае силно. Защото разглежданият интеграл в никакъв случай не е табличен - той се взема на части. Ние решаваме:
Прекъсваме решението за междинни обяснения.
Използваме формулата за интегриране по части: ![]()
Формулата се прилага отляво надясно
Гледаме лявата страна: . Очевидно в нашия пример (и във всички останали, които ще разгледаме) нещо трябва да бъде обозначено като , а нещо като .
В интегралите от разглеждания тип винаги се обозначава логаритъм.
Технически дизайнът на решението е реализиран, както следва, пишем в колоната:
Тоест, ние обозначихме логаритъма с и с - останалата частинтегранд израз.
Следващ етап: намерете диференциала:

Диференциалът е почти същият като производната; вече обсъдихме как да го намерим в предишните уроци.
Сега намираме функцията. За да намерите функцията, която трябва да интегрирате правилната странапо-ниско равенство:

Сега отваряме нашето решение и конструираме дясната страна на формулата: .
Между другото, ето извадка от крайното решение с някои бележки:

Единственият момент в работата е, че веднага размених и , тъй като е обичайно да се пише факторът преди логаритъма.
Както можете да видите, прилагането на формулата за интегриране по части по същество намали нашето решение до два прости интеграла.
Моля, имайте предвид, че в някои случаи веднага следприлагане на формулата, задължително се извършва опростяване под оставащия интеграл - в разглеждания пример ние намалихме интегранта до „x“.
Да проверим. За да направите това, трябва да вземете производната на отговора:
Получена е оригиналната интегрална функция, което означава, че интегралът е решен правилно.
По време на теста използвахме правилото за диференциране на продукта: ![]() . И това не е случайно.
. И това не е случайно.
Формула за интегриране по части ![]() и формула
и формула ![]() – това са две взаимно обратни правила.
– това са две взаимно обратни правила.
Пример 2
Намерете неопределения интеграл.
Интегралната функция е произведение на логаритъм и полином.
Нека решим.
![]()
Още веднъж ще опиша подробно процедурата за прилагане на правилото; в бъдеще примерите ще бъдат представени по-накратко и ако имате затруднения да го решите сами, трябва да се върнете към първите два примера от урока .
Както вече споменахме, необходимо е да се обозначи логаритъм (фактът, че е мощност, няма значение). Означаваме с останалата частинтегранд израз.
Пишем в колоната:
Първо намираме диференциала:

Тук използваме правилото за диференциране на сложна функция ![]() . Неслучайно още на първия урок от темата Неопределен интеграл. Примери за решенияФокусирах се върху факта, че за да овладеете интегралите, е необходимо да се „хванете“ за производни. Ще трябва да се справите с деривати повече от веднъж.
. Неслучайно още на първия урок от темата Неопределен интеграл. Примери за решенияФокусирах се върху факта, че за да овладеете интегралите, е необходимо да се „хванете“ за производни. Ще трябва да се справите с деривати повече от веднъж.
Сега намираме функцията, за това интегрираме правилната странапо-ниско равенство:

За интегриране използвахме най-простата таблична формула ![]()
Сега всичко е готово за прилагане на формулата ![]() . Отворете със звездичка и „конструирайте“ решението в съответствие с дясната страна:
. Отворете със звездичка и „конструирайте“ решението в съответствие с дясната страна:
Под интеграла отново имаме полином за логаритъм! Следователно решението отново се прекъсва и правилото за интегриране по части се прилага втори път. Не забравяйте, че в подобни ситуации логаритъма винаги се обозначава.

Би било добре, ако досега знаете как да намирате устно най-простите интеграли и производни.

(1) Не се бъркайте за знаците! Много често минусът се губи тук, имайте предвид също, че минусът се отнася за за всичкискоба  и тези скоби трябва да бъдат разгънати правилно.
и тези скоби трябва да бъдат разгънати правилно.
(2) Отворете скобите. Опростяваме последния интеграл.
(3) Взимаме последния интеграл.
(4) „Сресване“ на отговора.
Необходимостта да се приложи правилото за интегриране по части два пъти (или дори три пъти) не възниква много рядко.
А сега няколко примера за вашето собствено решение:
Пример 3
Намерете неопределения интеграл.
Този пример се решава чрез промяна на променливата (или заместването й под диференциалния знак)! Защо не - можете да опитате да го вземете на части, ще се окаже смешна работа.
Пример 4
Намерете неопределения интеграл.
Но този интеграл е интегриран с части (обещаната дроб).
Това са примери, които можете да решите сами, решения и отговори в края на урока.
Изглежда, че в примери 3 и 4 интеграндите са подобни, но методите за решаване са различни! Това е основната трудност при овладяването на интеграли - ако изберете грешен метод за решаване на интеграл, тогава можете да се занимавате с него с часове, като с истински пъзел. Следователно, колкото повече решавате различни интеграли, толкова по-добре, толкова по-лесно ще бъде тестът и изпитът. Освен това през втората година ще има диференциални уравнения, а без опит в решаването на интеграли и производни няма какво да се прави там.
По отношение на логаритмите това вероятно е повече от достатъчно. Като настрана, мога също да си спомня, че студентите по инженерство използват логаритми, за да наричат женски гърди =). Между другото, полезно е да знаете наизуст графиките на основните елементарни функции: синус, косинус, арктангенс, експонента, полиноми от трета, четвърта степен и др. Не, разбира се, презерватив на земното кълбо
Няма да го разтягам, но сега ще запомните много от раздела Графики и функции =).
Интеграли на експонента, умножена по полином
Общо правило:
Пример 5
Намерете неопределения интеграл.
![]()
Използвайки познат алгоритъм, ние интегрираме по части:


Ако имате затруднения с интеграла, тогава трябва да се върнете към статията Метод на промяна на променлива в неопределен интеграл.
Единственото друго нещо, което можете да направите, е да промените отговора:

Но ако техниката ви на изчисление не е много добра, тогава най-изгодният вариант е да го оставите като отговор ![]() или дори
или дори ![]()
Тоест примерът се счита за решен, когато се вземе последният интеграл. Няма да е грешка; друг е въпросът, че учителят може да ви помоли да опростите отговора.
Пример 6
Намерете неопределения интеграл.
Това е пример, който можете да решите сами. Този интеграл се интегрира два пъти по части. Особено внимание трябва да се обърне на знаците - лесно е да се объркате в тях, ние също помним, че това е сложна функция.
За изложителя няма какво повече да се каже. Мога само да добавя, че експоненциалът и натуралният логаритъм са взаимно обратни функции, това съм аз в темата за занимателни графики на висшата математика =) Спри, спри, не се притеснявай, лекторът е трезвен.
Интеграли на тригонометрични функции, умножени по полином
Общо правило: за винаги обозначава полином
Пример 7
Намерете неопределения интеграл.
![]()
Нека интегрираме по части:


Хм...и няма какво да коментираме.
Пример 8
Намерете неопределения интеграл ![]()
Това е пример, за да решите сами
Пример 9
Намерете неопределения интеграл
Още един пример с дроб. Както в предишните два примера, for обозначава полином.
Нека интегрираме по части: 

Ако имате затруднения или недоразумения при намирането на интеграла, препоръчвам ви да посетите урока Интеграли на тригонометрични функции.
Пример 10
Намерете неопределения интеграл ![]()
Това е пример, който можете да решите сами.
Съвет: Преди да използвате метода на интегриране по части, трябва да приложите някаква тригонометрична формула, която превръща произведението на две тригонометрични функции в една функция. Формулата може да се използва и при прилагане на метода на интегриране по части, както ви е по-удобно.
Това вероятно е всичко в този параграф. По някаква причина си спомних реплика от химна за физика и математика „И синусовата графика тече вълна след вълна по абсцисната ос“….
Интеграли на обратни тригонометрични функции.
Интеграли на обратни тригонометрични функции, умножени по полином
Общо правило: винаги обозначава обратната тригонометрична функция.
Нека ви напомня, че обратните тригонометрични функции включват арксинус, аркосинус, арктангенс и арккотангенс. За краткост на записа ще ги нарека "арки"

 към изчисляването на интеграла
към изчисляването на интеграла  , което се оказва по-просто от това.
, което се оказва по-просто от това. ,
, ,
, , Където
, Където  – полином,
– полином,  - число не равно на нула
- число не равно на нула обозначават полином
обозначават полином 
 .
. ,
, ,
, ,
, ,
, , Където
, Където  – полином.
– полином. обозначавам
обозначавам  , а останалата част от интегранта през
, а останалата част от интегранта през  :
: ,
, , Където
, Където  – числа.
– числа. обозначавам
обозначавам  и приложете формулата за интегриране по части два пъти, връщайки като резултат първоначалния интеграл, след което оригиналният интеграл се изразява от равенството.
и приложете формулата за интегриране по части два пъти, връщайки като резултат първоначалния интеграл, след което оригиналният интеграл се изразява от равенството. ; б)
; б)  .
.
 , Където
, Където  – полином на степен
– полином на степен  ,
, – полином на степен
– полином на степен
 .
. , в противен случай (ако
, в противен случай (ако  ) се нарича рационална дроб грешно.
) се нарича рационална дроб грешно. и правилна рационална дроб чрез разделяне на числителя на знаменателя съгласно правилото за деление на полиноми:
и правилна рационална дроб чрез разделяне на числителя на знаменателя съгласно правилото за деление на полиноми: ,
, – цяла част от деление,
– цяла част от деление,  – правилна рационална дроб,
– правилна рационална дроб,  - остатък от делението.
- остатък от делението. ;
; ;
; ;
; ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 – реални числа и
– реални числа и  (т.е. квадратният тричлен в знаменателя на III и IV дроби няма корени - дискриминантът е отрицателен) се наричат прости рационални дроби I, II, III и IV видове.
(т.е. квадратният тричлен в знаменателя на III и IV дроби няма корени - дискриминантът е отрицателен) се наричат прости рационални дроби I, II, III и IV видове. .
. .
. . След заместването интегралът се разделя на два интеграла. Първият интеграл се изчислява чрез изолиране на производната на знаменателя в числителя, което дава табличен интеграл, а вторият интеграл се преобразува във формата
. След заместването интегралът се разделя на два интеграла. Първият интеграл се изчислява чрез изолиране на производната на знаменателя в числителя, което дава табличен интеграл, а вторият интеграл се преобразува във формата  , защото
, защото  , което също дава табличния интеграл.
, което също дава табличния интеграл.

 ;
; . След заместването интегралът се разделя на два интеграла. Първият интеграл се изчислява чрез заместване
. След заместването интегралът се разделя на два интеграла. Първият интеграл се изчислява чрез заместване  , а вторият използва рекурентни отношения.
, а вторият използва рекурентни отношения. ; б)
; б)  ; V)
; V)  .
. .
. съответства на една част от формата
съответства на една част от формата  ;
; отговаря на сумата
отговаря на сумата  дроби от формата
дроби от формата съответства на част от формата
съответства на част от формата  ;
; отговаря на сумата
отговаря на сумата  дроби от формата
дроби от формата . Приравняване на коефициенти при еднакви степени
. Приравняване на коефициенти при еднакви степени  в полиномите на лявата и дясната страна, получаваме система от линейни уравнения. При решаването на системата определяме несигурните коефициенти.
в полиномите на лявата и дясната страна, получаваме система от линейни уравнения. При решаването на системата определяме несигурните коефициенти. от лявата и дясната страна на всяко число, получаваме истинско равенство, линейно по отношение на неизвестните коефициенти. Подмяна на толкова много стойности
от лявата и дясната страна на всяко число, получаваме истинско равенство, линейно по отношение на неизвестните коефициенти. Подмяна на толкова много стойности  , колко неизвестни коефициента има, получаваме система от линейни уравнения. Вместо
, колко неизвестни коефициента има, получаваме система от линейни уравнения. Вместо  Можете да замените всякакви числа в лявата и дясната страна, но е по-удобно да замените корените на знаменателите на дробите.
Можете да замените всякакви числа в лявата и дясната страна, но е по-удобно да замените корените на знаменателите на дробите. ; б)
; б)  ; V)
; V)  .
. .
.
 .
. , получаваме:
, получаваме:



 .
. .
. .
. .
. , получаваме системата:
, получаваме системата:








 .
.
 .
. .
. .
. частични стойности, при които факторите изчезват, т.е. заместваме тези стойности в последния израз и получаваме три уравнения:
частични стойности, при които факторите изчезват, т.е. заместваме тези стойности в последния израз и получаваме три уравнения:
 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.


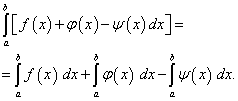 (42)
(42)




