Биномиальное распределение дискретной случайной величины.
Здравствуйте! Мы уже знаем, что такое распределение вероятностей. Оно может быть дискретным или непрерывным, и мы узнали, что его называют плотностью распределения вероятностей. Теперь давайте изучим парочку более распространенных распределений. Предположим, у меня есть монета, причем правильная монета, и я собираюсь ее подбросить 5 раз. Также я определю случайную величину Х, обозначу ее заглавной буквой X, она будет равна количеству «орлов» при 5 подбрасываниях. Может, у меня есть 5 монет, я подброшу их все сразу и посчитаю, сколько у меня выпало «орлов». Или у меня могла бы быть одна монета, я могла бы ее подбросить 5 раз и посчитать, сколько раз у меня выпал «орел». Это, собственно, не имеет значения. Но давайте предположим, что у меня одна монета, и я подброшу ее 5 раз. Тогда у нас не будет неопределенности. Итак, вот определение моей случайной величины. Как мы знаем, случайная величина немного отличается от обычной переменной, она больше похожа на функцию. Она присваивает какое-то значение эксперименту. И эта случайная величина довольно проста. Мы просто считаем, сколько раз выпал «орел» после 5 подбрасываний, – это и есть наша случайная величина X. Давайте подумаем, какие могут быть вероятности разных значений в нашем случае? Так, какова вероятность того, что Х (заглавная Х) равна 0? Т.е. какова вероятность того, что после 5 подбрасываний ни разу не выпадет «орел»? Ну, это, по сути, то же самое, что вероятность выпадения одних «решек» (это так, небольшой обзор теории вероятностей). У вас должны выпасть одни «решки». Какова вероятность каждой из этих «решек»? Это 1/2. Т.е. здесь должно быть 1/2 умножить на 1/2, на 1/2, на 1/2 и снова на 1/2. Т.е. (1/2)⁵. 1⁵=1, разделить на 2⁵, т.е. на 32. Вполне логично. Так… Я немного повторю то, что мы проходили по теории вероятностей. Это важно для того, чтобы понимать, куда мы сейчас движемся и как, собственно, формируется дискретное распределение вероятностей. Итак, а какова вероятность того, что у нас ровно 1 раз выпадет «орел»? Ну, «орел» мог бы выпасть при первом подбрасывании. Т.е. могло бы быть так: «орел», «решка», «решка», «решка», «решка». Или «орел» мог бы выпасть при втором подбрасывании. Т.е. могла бы быть такая комбинация: «решка», «орел», «решка», «решка», «решка» и так далее. Один «орел» мог бы выпасть после любого из 5 подбрасываний. Какова вероятность каждой из этих ситуаций? Вероятность выпадения «орла» равна 1/2. Затем вероятность выпадения «решки», равная 1/2, умножить на 1/2, на 1/2, на 1/2. Т.е. вероятность каждой из этих ситуаций равна 1/32. Так же, как и вероятность ситуации, где Х=0. По сути, вероятность любого особого порядка выпадений «орла» и «решки» будет равна 1/32. Итак, вероятность этого равна 1/32. И вероятность этого равна 1/32. И вот такие ситуации имеют место потому, что «орел» мог бы выпасть при любом из 5 подбрасываний. Следовательно, вероятность того, что точно выпадет один «орел», равна 5*1/32, т.е. 5/32. Вполне логично. Теперь начинается интересное. Какова вероятность… (буду писать каждый из примеров другим цветом)… какова вероятность того, что моя случайная величина равна 2? Т.е. я подброшу монету 5 раз, и какова вероятность того, что 2 раза точно выпадет «орел»? Это уже интереснее, правда? Какие возможны комбинации? Могла бы быть «орел», «орел», «решка», «решка», «решка». Также могла бы быть «орел», «решка», «орел», «решка», «решка». И если подумать, что эти два «орла» могут стоять в разных местах комбинации, то можно немного запутаться. Уже нельзя размышлять о размещениях так, как мы это делали здесь, вверху. Хотя… можно, только рискуете запутаться. Вы должны понять одно. Для каждой из этих комбинаций вероятность равна 1/32. ½*½*½*½*½. Т.е. вероятность каждой из этих комбинаций равна 1/32. И мы должны подумать над тем, сколько существует таких комбинаций, удовлетворяющих нашему условию (2 «орла»)? Т.е. по сути, нужно представить, что есть 5 подбрасываний монеты, и нужно из них выбрать 2, при которых выпадает «орел». Давайте представим, что наши 5 подбрасываний собрались в кружочек, также представим, что у нас есть только два стула. И мы говорим: «Хорошо, кто из вас сядет на эти стулья для «орлов»? Т.е. кто из вас будет «орлом»? И нас не интересует то, в каком порядке они сядут. Я привожу такой пример, надеясь, что так вам будет понятнее. И может, вам захочется посмотреть некоторые уроки по теории вероятностей на эту тему, когда я буду говорить о биноме Ньютона. Потому что там я более детально углублюсь во все это. Но если вы будете рассуждать таким путем, то поймете, что такое биномиальный коэффициент. Потому что если будете думать так: хорошо, у меня 5 подбрасываний, при каком подбрасывании выпадет первый «орел»? Ну, здесь 5 возможностей того, при каком по счету подбрасывании выпадет первый «орел». А сколько возможностей для второго «орла»? Ну, первое подбрасывание, которое мы уже использовали, забрало одну возможность выпадения «орла». Т.е. одна позиция «орла» в комбинации уже занята одним из подбрасываний. Теперь осталось 4 подбрасывания, значит, второй «орел» может выпасть при одном из 4 подбрасываний. И вы это видели, вот здесь. Я выбрала так, что «орел» выпал при 1-м подбрасывании, и предположила, что при 1 из 4 оставшихся бросков также должен выпасть «орел». Итак, здесь только 4 возможности. Все, что я говорю, означает, что для первого «орла» у вас есть 5 различных позиций, на которые он может выпасть. А для второго уже остается только 4 позиции. Подумайте над этим. Когда мы вычисляем вот так, то порядок учитывается. Но для нас сейчас неважно, в какой последовательности выпадают «орлы» и «решки». Мы не говорим, что это «орел 1» или что это «орел 2». В обоих случаях это просто «орел». Мы могли бы предположить, что это «орел 1», а это – «орел 2». Или могло бы быть наоборот: это мог бы быть второй «орел», а это – «первый». И я говорю это потому, что важно понять, где использовать размещения, а где – сочетания. Нас не интересует последовательность. Так что, собственно, есть только 2 способа происхождения нашего события. Значит, делим это на 2. И как вы позже увидите, здесь 2! способов происхождения нашего события. Если было бы 3 «орла», тогда здесь было бы 3!, и я покажу вам, почему. Итак, это будет равно… 5*4=20 и разделить на 2 – получится 10. Поэтому здесь 10 различных комбинаций из 32, в которых у вас точно будет 2 «орла». Итак, 10*(1/32) равно 10/32, а чему это равно? 5/16. Запишу через биномиальный коэффициент. Это значение, вот здесь, вверху. Если подумать, то это – то же самое, что и 5!, деленный на… Что означает вот это 5*4? 5! – это 5*4*3*2*1. Т.е. если мне здесь нужно только 5*4, то для этого я могу разделить 5! на 3! Это равно 5*4*3*2*1, деленное на 3*2*1. И остается только 5*4. Значит, это – то же самое, что и этот числитель. И затем, т.к. нас не интересует последовательность, нам нужно здесь 2. Собственно, 2!. Умножить на 1/32. Такой была бы вероятность того, что у нас выпало бы точно 2 «орла». Какова вероятность того, что у нас точно 3 раза выпадет «орел»? Т.е. вероятность того, что Х=3. Итак, по той же логике, первый случай выпадения «орла» может иметь место при 1 из 5 подбрасываний. Второй случай выпадения «орла» может иметь место при 1 из 4 оставшихся подбрасываний. А третий случай выпадения «орла» может иметь место при 1 из 3 оставшихся подбрасываний. А сколько существует различных способов расставить 3 подбрасывания? В общем, сколько есть способов, чтобы расставить 3 предмета по местам? Это 3! И вы можете это вычислить или, возможно, захотите пересмотреть те уроки, в которых я подробнее это объясняла. Но если вы, например, возьмете буквы A, B и C, то всего есть 6 способов, с помощью которых вы их можете расставить. Можете рассматривать это как случаи выпадения «орлов». Здесь могли бы быть ACB, CAB. Могло бы быть BAC, BCA, и… Какой последний вариант, который я не назвала? CBA. Есть 6 способов расставить 3 разных предмета. Мы делим на 6, потому что не хотим повторно засчитывать эти 6 разных способов, потому что рассматриваем их как равнозначные. Здесь нас не интересует, при каком по счету подбрасывании выпадет «орел». 5*4*3… Это можно переписать, как 5!/2!. И разделить это еще на 3!. Это он и есть. 3! равен 3*2*1. Тройки сокращаются. Это становится равным 2. Это – равным 1. Еще раз, 5*2, т.е. равно 10. Каждая ситуация имеет вероятность 1/32, потому это опять равно 5/16. И это интересно. Вероятность того, что у вас выпадет 3 «орла» равна вероятности того, что у вас есть 2 орла. И причина этому… Ну, есть много причин тому, что так получилось. Но если подумать, что вероятность того, что выпадет 3 «орла» – то же самое, что вероятность выпадения 2 «решек». И вероятность выпадения 3 «решек» должна быть такой же, как и вероятность выпадения 2-х «орлов». И хорошо, что значения вот так срабатывают. Хорошо. Какова вероятность того, что Х=4? Мы можем использовать ту же формулу, что использовали прежде. Это могло бы быть 5*4*3*2. Итак, здесь запишем 5*4*3*2… Сколько есть различных способов расставить 4 предмета? Это 4!. 4! – это, по сути, вот эта часть, вот здесь. Это 4*3*2*1. Так, это сокращается, остается 5. Затем, каждая комбинация имеет вероятность 1/32. Т.е. это равно 5/32. И еще раз заметьте, что вероятность того, что 4 раза выпадет «орел» равна вероятности того, что 1 раз выпадет «орел». И в этом есть смысл, т.к. 4 «орла» – это то же самое, что случай выпадения 1 «решки». Вы скажете: ну, и при каком же подбрасывании выпадет эта одна «решка»? Ага, для этого здесь есть 5 различных комбинаций. И каждая из них имеет вероятность 1/32. И наконец, какова вероятность того, что Х=5? Т.е. выпадает «орел» 5 раз подряд. Должно быть так: «орел», «орел», «орел», «орел», «орел». Каждый из «орлов» имеет вероятность 1/2. Вы их перемножаете и получаете 1/32. Можно пойти другим путем. Если всего есть 32 способа, с помощью которых вы можете получить «орлы» и «решки» в этих экспериментах, то это – только один из этих способов. Здесь таких способов было 5 из 32. Здесь - 10 из 32. Тем не менее, вычисления мы провели, а теперь готовы нарисовать распределение вероятностей. Но мое время истекло. Позвольте продолжить на следующем уроке. А если вы в настроении, то, может, нарисуете перед тем, как смотреть следующий урок? До скорой встречи!
Биномиальное распределение - одно из важнейших распределений вероятностей дискретно изменяющейся случайной величины. Биномиальным распределением называется распределение вероятностей числа m наступления события А в n взаимно независимых наблюдениях . Часто событие А называют "успехом" наблюдения, а противоположное ему событие - "неуспехом", но это обозначение весьма условное.
Условия биномиального распределения :
- в общей сложности проведено n испытаний, в которых событие А может наступить или не наступить;
- событие А в каждом из испытаний может наступить с одной и той же вероятностью p ;
- испытания являются взаимно независимыми.
Вероятность того, что в n испытаниях событие А наступит именно m раз, можно вычислить по формуле Бернулли:
,
где p - вероятность наступления события А ;
q = 1 - p - вероятность наступления противоположного события .
Разберёмся, почему биномиальное распределение описанным выше образом связано с формулой Бернулли . Событие - число успехов при n испытаниях распадается на ряд вариантов, в каждом из которых успех достигается в m испытаниях, а неуспех - в n - m испытаниях. Рассмотрим один из таких вариантов - B 1 . По правилу сложения вероятностей умножаем вероятности противоположных событий:
,
а если обозначим q = 1 - p , то
.
Такую же вероятность будет иметь любой другой вариант, в котором m успехов и n - m неуспехов. Число таких вариантов равно - числу способов, которыми можно из n испытаний получить m успехов.
Сумма вероятностей всех m чисел наступления события А (чисел от 0 до n ) равна единице:
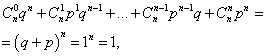
где каждое слагаемое представляет собой слагаемое бинома Ньютона. Поэтому рассматриваемое распределение и называется биномиальным распределением.
На практике часто необходимо вычислять вероятности "не более m успехов в n испытаниях" или "не менее m успехов в n испытаниях". Для этого используются следующие формулы.
Интегральную функцию, то есть вероятность F (m ) того, что в n наблюдениях событие А наступит не более m раз , можно вычислить по формуле:
В свою очередь вероятность F (≥m ) того, что в n наблюдениях событие А наступит не менее m раз , вычисляется по формуле:
Иногда бывает удобнее вычислять вероятность того, что в n наблюдениях событие А наступит не более m раз, через вероятность противоположного события:
.
Какой из формул пользоваться, зависит от того, в какой из них сумма содержит меньше слагаемых.
Характеристики биномиального распределения вычисляются по следующим формулам .
Математическое ожидание: .
Дисперсия: .
Среднеквадратичное отклонение: .
Биномиальное распределение и расчёты в MS Excel
Вероятность биномиального распределения P n (m ) и значения интегральной функции F (m ) можно вычислить при помощи функции MS Excel БИНОМ.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши).
MS Excel требует ввести следующие данные:
- число успехов;
- число испытаний;
- вероятность успеха;
- интегральная - логическое значение: 0 - если нужно вычислить вероятность P n (m ) и 1 - если вероятность F (m ).
Пример 1. Менеджер фирмы обобщил информацию о числе проданных в течение последних 100 дней фотокамер. В таблице обобщена информация и рассчитаны вероятности того, что в день будет продано определённое число фотокамер.
День завершён с прибылью, если продано 13 или более фотокамер. Вероятность, что день будет отработан с прибылью:
Вероятность того, что день будет отработан без прибыли:
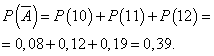
Пусть вероятность того, что день отработан с прибылью, является постоянной и равна 0,61, и число проданных в день фотокамер не зависит от дня. Тогда можно использовать биномиальное распределение, где событие А - день будет отработан с прибылью, - без прибыли.
Вероятность того, что из 6 дней все будут отработаны с прибылью:
.
Тот же результат получим, используя функцию MS Excel БИНОМ.РАСП (значение интегральной величины - 0):
P 6 (6 ) = БИНОМ.РАСП(6; 6; 0,61; 0) = 0,052.
Вероятность того, что из 6 дней 4 и больше дней будут отработаны с прибылью:
где 
,
,
Используя функцию MS Excel БИНОМ.РАСП, вычислим вероятность того, что из 6 дней не более 3 дней будут завершены с прибылью (значение интегральной величины - 1):
P 6 (≤3 ) = БИНОМ.РАСП(3; 6; 0,61; 1) = 0,435.
Вероятность того, что из 6 дней все будут отработаны с убытками:
,
Тот же показатель вычислим, используя функцию MS Excel БИНОМ.РАСП:
P 6 (0 ) = БИНОМ.РАСП(0; 6; 0,61; 0) = 0,0035.
Решить задачу самостоятельно, а затем посмотреть решение
Пример 2. В урне 2 белых шара и 3 чёрных. Из урны вынимают шар, устанавливают цвет и кладут обратно. Попытку повторяют 5 раз. Число появления белых шаров - дискретная случайная величина X , распределённая по биномиальному закону. Составить закон распределения случайной величины. Определить моду, математическое ожидание и дисперсию.
Продолжаем решать задачи вместе
Пример 3. Из курьерской службы отправились на объекты n = 5 курьеров. Каждый курьер с вероятностью p = 0,3 независимо от других опаздывает на объект. Дискретная случайная величина X - число опоздавших курьеров. Построить ряд распределения это случайной величины. Найти её математическое ожидание, дисперсию, среднее квадратическое отклонение. Найти вероятность того, что на объекты опоздают не менее двух курьеров.
Конечно, при вычислении кумулятивной функции распределения следует воспользоваться упомянутой связью биномиального и бета- распределения. Этот способ заведомо лучше непосредственного суммирования, когда n > 10.
В классических учебниках по статистике для получения значений биномиального распределения часто рекомендуют использовать формулы, основанные на предельных теоремах (типа формулы Муавра-Лапласа). Необходимо отметить, что с чисто вычислительной точки зрения ценность этих теорем близка к нулю, особенно сейчас, когда практически на каждом столе стоит мощный компьютер. Основной недостаток приведенных аппроксимаций – их совершенно недостаточная точность при значениях n, характерных для большинства приложений. Не меньшим недостатком является и отсутствие сколько-нибудь четких рекомендаций о применимости той или иной аппроксимации (в стандартных текстах приводятся лишь асимптотические формулировки, они не сопровождаются оценками точности и, следовательно, мало полезны). Я бы сказал, что обе формулы пригодны лишь при n < 200 и для совсем грубых, ориентировочных расчетов, причем делаемых “вручную” с помощью статистических таблиц. А вот связь между биномиальным распределением и бета-распределением позволяет вычислять биномиальное распределение достаточно экономно.
Я не рассматриваю здесь задачу поиска квантилей: для дискретных распределений она тривиальна, а в тех задачах, где такие распределения возникают, она, как правило, и не актуальна. Если же квантили все-таки понадобятся, рекомендую так переформулировать задачу, чтобы работать с p-значениями (наблюденными значимостями). Вот пример: при реализации некоторых переборных алгоритмов на каждом шаге требуется проверять статистическую гипотезу о биномиальной случайной величине. Согласно классическому подходу на каждом шаге нужно вычислить статистику критерия и сравнить ее значение с границей критического множества. Поскольку, однако, алгоритм переборный, приходится определять границу критического множества каждый раз заново (ведь от шага к шагу объем выборки меняется), что непроизводительно увеличивает временные затраты. Современный подход рекомендует вычислять наблюденную значимость и сравнивать ее с доверительной вероятностью, экономя на поиске квантилей.
Поэтому в приводимых ниже кодах отсутствует вычисление обратной функции, взамен приведена функция rev_binomialDF , которая вычисляет вероятность p успеха в отдельном испытании по заданному количеству n испытаний, числу m успехов в них и значению y вероятности получить эти m успехов. При этом используется вышеупомянутая связь между биномиальным и бета распределениями.
Фактически, эта функция позволяет получать границы доверительных интервалов.
В самом деле, предположим, что в n
биномиальных испытаниях мы получили m
успехов. Как известно, левая граница двухстороннего доверительного интервала
для параметра p с доверительным уровнем
равна 0, если
m = 0, а для
является решением уравнения 
.
Аналогично, правая граница равна 1,
если m = n, а для
является решением уравнения 
.
Отсюда вытекает, что для поиска левой границы мы должны решать относительно
уравнение
,
а для поиска правой – уравнение
.
Они и решаются в функциях binom_leftCI и binom_rightCI ,
возвращающих верхнюю и нижнюю границы двустороннего доверительного интервала
соответственно.
Хочу заметить, что если не нужна совсем уж неимоверная точность, то
при достаточно больших n можно воспользоваться
следующей аппроксимацией [Б.Л. ван дер Варден, Математическая статистика.
М: ИЛ, 1960, гл. 2, разд. 7]:
,
где g – квантиль нормального распределения.
Ценность этой аппроксимации в том, что имеются очень простые приближения,
позволяющие вычислять квантили нормального распределения (см. текст о вычислении
нормального распределения и соответствующий раздел данного справочника).
В моей практике (в основном, при n > 100) эта аппроксимация давала примерно 3-4 знака, чего, как правило,
вполне достаточно.
Для вычислений с помощью нижеследующих кодов потребуются файлы betaDF.h , betaDF.cpp (см. раздел о бета-распределении), а также logGamma.h , logGamma.cpp (см. приложение А). Вы можете посмотреть также пример использования функций.
Файл binomialDF.h
| #ifndef __BINOMIAL_H__ #include "betaDF.h" double binomialDF(double trials, double successes, double p); /* * Пусть имеется "trials" независимых наблюдений * с вероятностью "p" успеха в каждом. * Вычисляется вероятность B(successes|trials,p) того, что число * успехов заключено между 0 и "successes" (включительно). */ double rev_binomialDF(double trials, double successes, double y); /* * Пусть известна вероятность y наступления не менее m успехов * в trials испытаниях схемы Бернулли. Функция находит вероятность p * успеха в отдельном испытании. * * В вычислениях используется следующее соотношение * * 1 - p = rev_Beta(trials-successes| successes+1, y). */ double binom_leftCI(double trials, double successes, double level); /* Пусть имеется "trials" независимых наблюдений * с вероятностью "p" успеха в каждом * и количество успехов равно "successes". * Вычисляется левая граница двустороннего доверительного интервала * с уровнем значимости level. */ double binom_rightCI(double n, double successes, double level); /* Пусть имеется "trials" независимых наблюдений * с вероятностью "p" успеха в каждом * и количество успехов равно "successes". * Вычисляется правая граница двустороннего доверительного интервала * с уровнем значимости level. */ #endif /* Ends #ifndef __BINOMIAL_H__ */ |
Файл binomialDF.cpp
|
/***********************************************************/
/* Биномиальное распределение */
/***********************************************************/
#include |
Распределения вероятностей дискретных случайных величин. Биномиальное распределение. Распределение Пуассона. Геометрическое распределение. Производящая функция.
6. Распределения вероятностей дискретных случайных величин
6.1. Биномиальное распределение
Пусть производится n независимых испытаний, в каждом из которых событие A может либо появится, либо не появится. Вероятность p появления события A во всех испытаниях постоянна и не изменяется от испытания к испытанию. Рассмотрим в качестве случайной величины X число появлений события A в этих испытаниях. Формула, позволяющая найти вероятность появления события A ровно k раз в n испытаниях, как известно, описывается формулой Бернулли
Распределение вероятностей, определяемое формулой Бернулли, называется биномиальным .
Этот закон назван "биномиальным" потому, что правую часть можно рассматривать как общий член разложения бинома Ньютона
Запишем биномиальный закон в виде таблицы
|
p n |
np n –1 q |
|
q n |
Найдем числовые характеристики этого распределения.
По определению математического ожидания для ДСВ имеем
.
Запишем равенство, являющееся бином Ньютона
.
и продифференцируем его по p. В результате получим
.
Умножим левую и правую часть на p :
.
Учитывая, что p + q =1, имеем
(6.2)
Итак, математическое ожидание числа появлений событий в n независимых испытаниях равно произведению числа испытаний n на вероятность p появления события в каждом испытании .
Дисперсию вычислим по формуле
.
Для этого найдем
.
Предварительно продифференцируем формулу бинома Ньютона два раза по p :
и умножим обе части равенства на p 2:
Следовательно,
Итак, дисперсия биномиального распределения равна
.
(6.3)
Данные результаты можно получить и из чисто качественных рассуждений. Общее число X появлений события A во всех испытаниях складываются из числа появлений события в отдельных испытаниях. Поэтому если X 1 – число появлений события в первом испытании, X 2 – во втором и т.д., то общее число появлений события A во всех испытаниях равно X=X 1 +X 2 +…+X n . По свойству математического ожидания:
Каждое из слагаемых правой части равенства есть математическое ожидание числа событий в одном испытании, которое равно вероятности события. Таким образом,
По свойству дисперсии:
Так
как
,
а математическое ожидание случайной
величины
,
которое может принимать только два
значения, а именно 1 2
с вероятностью p
и 0 2
с вероятностью q
,
то
.
Таким образом,
В результате, получаем
Воспользовавшись понятием начальных и центральных моментов, можно получить формулы для асимметрии и эксцесса:
.
(6.4)
Рис. 6.1
Многоугольник биномиального распределения имеет следующий вид (см. рис. 6.1). ВероятностьP n (k ) сначала возрастает при увеличении k , достигает наибольшего значения и далее начинает убывать. Биномиальное распределение асимметрично, за исключением случая p =0,5. Отметим, что при большом числе испытаний n биномиальное распределение весьма близко к нормальному. (Обоснование этого предложения связано с локальной теоремой Муавра-Лапласа.)Число m 0 наступлений события называется наивероятнейшим , если вероятность наступления события данное число раз в этой серии испытаний наибольшая (максимум в многоугольнике распределения) . Для биномиального распределения
Замечание. Данное неравенство можно доказать, используя рекуррентную формулу для биномиальных вероятностей:
(6.6)
Пример 6.1. Доля изделий высшего сорта на данном предприятии составляет 31%. Чему равно математического ожидание и дисперсия, также наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 75 изделий?
Решение. Поскольку p =0,31, q =0,69, n =75, то
M[X ] = np = 750,31 = 23,25; D[X ] = npq = 750,310,69 = 16,04.
Для нахождения наивероятнейшего числа m 0 , составим двойное неравенство
Отсюда следует, что m 0 = 23.
В настоящей и нескольких следующих заметках мы рассмотрим математические модели случайных событий. Математическая модель - это математическое выражение, представляющее случайную величину. Для дискретных случайных величин это математическое выражение известно под названием функция распределения.
Если задача позволяет явно записать математическое выражение, представляющее случайную величину, можно вычислить точную вероятность любого ее значения. В этом случае можно вычислить и перечислить все значения функции распределения. В деловых, социологических и медицинских приложениях встречаются разнообразные распределения случайных величин. Одним из наиболее полезных распределений является биномиальное.
Биномиальное распределение используется для моделирования ситуаций, характеризующихся следующими особенностями.
- Выборка состоит из фиксированного числа элементов n , представляющих собой исходы некоего испытания.
- Каждый элемент выборки принадлежит одной из двух взаимоисключающих категорий, исчерпывающих все выборочное пространство. Как правило, эти две категории называют успех и неудача.
- Вероятность успеха р является постоянной. Следовательно, вероятность неудачи равна 1 – р .
- Исход (т.е. удача или неудача) любого испытания не зависит от результата другого испытания. Чтобы гарантировать независимость исходов, элементы выборки, как правило, получают с помощью двух разных методов. Каждый элемент выборки случайным образом извлекается из бесконечной генеральной совокупности без возвращения или из конечной генеральной совокупности с возвращением.
Скачать заметку в формате или , примеры в формате
Биномиальное распределение используется для оценки количества успехов в выборке, состоящей из n наблюдений. Рассмотрим в качестве примера оформление заказов. Чтобы сделать заказ клиенты компании Saxon Company могут воспользоваться интерактивной электронной формой и послать ее в компанию. Затем информационная система проверяет, нет ли в заказах ошибок, а также неполной или недостоверной информации. Любой заказ, вызывающий сомнения, помечается и включается в ежедневный отчет об исключительных ситуациях. Данные, собранные компанией, свидетельствуют, что вероятность ошибок в заказах равна 0,1. Компания хотела бы знать, какова вероятность обнаружить определенное количество ошибочных заказов в заданной выборке. Например, предположим, что клиенты заполнили четыре электронных формы. Какова вероятность, что все заказы окажутся безошибочными? Как вычислить эту вероятность? Под успехом будем понимать ошибку при заполнении формы, а все остальные исходы будем считать неудачей. Напомним, что нас интересует количество ошибочных заказов в заданной выборке.
Какие исходы мы можем наблюдать? Если выборка состоит из четырех заказов, ошибочными могут оказаться один, два, три или все четыре, кроме того, все они могут оказаться правильно заполненными. Может ли случайная величина, описывающая количество неправильно заполненных форм, принимать какое-либо иное значение? Это невозможно, поскольку количество неправильно заполненных форм не может превышать объем выборки n или быть отрицательным. Таким образом, случайная величина, подчиняющаяся биномиальному закону распределения, принимает значения от 0 до n .
Допустим, что в выборке из четырех заказов наблюдаются следующие исходы:
Какова вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, причем в указанной последовательности? Поскольку предварительные исследования показали, что вероятность ошибки при заполнении формы равна 0,10, вероятности указанных выше исходов вычисляются следующим образом:
Поскольку исходы не зависят друг от друга, вероятность указанной последовательности исходов равна: р*р*(1–р)*р = 0,1*0,1*0,9*0,1 = 0,0009. Если же необходимо вычислить количество вариантов выбора X n элементов, следует воспользоваться формулой сочетаний (1):
где n! = n * (n –1) * (n – 2) * … * 2 * 1 - факториал числа n , причем 0! = 1 и 1! = 1 по определению.
Это выражение часто обозначают как . Таким образом, если n = 4 и X = 3, количество последовательностей, состоящих из трех элементов, извлеченных из выборки, объем которой равен 4, определяется по следующей формуле:
Следовательно, вероятность обнаружить три ошибочных заказа вычисляется следующим образом:
(Количество возможных последовательностей) *
(вероятность конкретной последовательности) = 4 * 0,0009 = 0,0036
Аналогично можно вычислить вероятность того, что среди четырех заказов окажутся один или два ошибочных, а также вероятность того, что все заказы ошибочны или все верны. Однако при увеличении объема выборки n определить вероятность конкретной последовательности исходов становится труднее. В этом случае следует применить соответствующую математическую модель, описывающую биномиальное распределение количества вариантов выбора X объектов из выборки, содержащей n элементов.
Биноминальное распределение
где Р(Х) - вероятность X успехов при заданных объеме выборки n и вероятности успеха р , X = 0, 1, … n .
Обратите внимание на то, что формула (2) представляет собой формализацию интуитивных выводов. Случайная величина X , подчиняющаяся биномиальному распределению, может принимать любое целое значение в диапазоне от 0 до n . Произведение р X (1 – р) n – X представляет собой вероятность конкретной последовательности, состоящей из X успехов в выборке, объем которой равен n . Величина определяет количество возможных комбинаций, состоящих из X успехов в n испытаниях. Следовательно, при заданном количестве испытаний n и вероятности успеха р вероятность последовательности, состоящей из X успехов, равна
Р(Х) = (количество возможных последовательностей) * (вероятность конкретной последовательности) =
Рассмотрим примеры, иллюстрирующие применение формулы (2).
1. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм три окажутся ошибочными? Используя формулу (2), получаем, что вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, равна
2. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными? Как показано в предыдущем примере, вероятность того, что среди четырех заполненных форм три окажутся ошибочными, равна 0,0036. Чтобы вычислить вероятность того, что среди четырех заполненных форм не менее трех будут неправильно заполнены, необходимо сложить вероятность того, что среди четырех заполненных форм три окажутся ошибочными, и вероятность того, что среди четырех заполненных форм все окажутся ошибочными. Вероятность второго события равна
Таким образом, вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными, равна
Р(Х > 3) = Р(Х = 3) + Р(Х = 4) = 0,0036 + 0,0001 = 0,0037
3. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм менее трех окажутся ошибочными? Вероятность этого события
Р(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)
Используя формулу (2), вычислим каждую из этих вероятностей:
Следовательно, Р(Х < 3) = 0,6561 + 0,2916 + 0,0486 = 0,9963.
Вероятность Р(Х < 3) можно вычислить иначе. Для этого воспользуемся тем, что событие X < 3 является дополнительным по отношению к событию Х> 3. Тогда Р(Х< 3) = 1 – Р(Х> 3) = 1 – 0,0037 = 0,9963.
По мере увеличения объема выборки n вычисления, аналогичные проведенным в примере 3, становятся затруднительными. Чтобы избегать этих сложностей, многие биномиальные вероятности табулируют заранее. Некоторые из этих вероятностей приведены рис. 1. Например, чтобы получить вероятность, что Х = 2 при n = 4 и p = 0,1, следует извлечь из таблицы число, стоящее на пересечении строки Х = 2 и столбца р = 0,1.
Рис. 1. Биномиальная вероятность при n = 4, Х = 2 и р = 0,1
Биномиальное распределение можно вычислить с помощью функции Excel =БИНОМ.РАСП() (рис. 2), имеющей 4 параметра: число успехов – Х , число испытаний (или объем выборки) – n , вероятность успеха – р , параметр интегральная , принимающий значения ИСТИНА (в этом случае вычисляется вероятность не менее Х событий) или ЛОЖЬ (в этом случае вычисляется вероятность точно Х событий).
Рис. 2. Параметры функции =БИНОМ.РАСП()
Для вышеприведенных трех примеров расчеты приведены на рис. 3 (см. также Excel-файл). В каждом столбце приведено по одной формуле. Цифрами показаны ответы на примеры соответствующего номера).
Рис. 3. Расчет биноминального распределения в Excel для n = 4 и p = 0,1
Свойства биномиального распределения
Биномиальное распределение зависит от параметров n и р . Биномиальное распределение может быть, как симметричным, так и асимметричным. Если р = 0,05, биномиальное распределение является симметричным независимо от величины параметра n . Однако, если р ≠ 0,05, распределение становится асимметричным. Чем ближе значение параметра р к 0,05 и чем больше объем выборки n , тем слабее выражена асимметрия распределения. Таким образом, распределение количества неправильно заполненных форм смещено вправо, поскольку p = 0,1 (рис. 4).
Рис. 4. Гистограмма биномиального распределения при n = 4 и p = 0,1
Математическое ожидание биномиального распределения равно произведению объема выборки n на вероятность успеха р :
(3) Μ = Е(Х) = np
В среднем, при достаточно долгой серии испытаний в выборке, состоящей из четырех заказов, может оказаться р = Е(Х) = 4 х 0,1 = 0,4 неправильно заполненных форм.
Стандартное отклонение биномиального распределения
Например, стандартное отклонение количества неверно заполненных форм в бухгалтерской информационной системе равно:
Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 307–313
